| № п/п | задание | ||||||||||||||||
| Отделить корни уравнения f(x)=0 аналитически. Выполнить программную реализацию уточнения двух корней методом касательных (Ньютона) с точностью ε=0,001. x3 – 0,1x2 + 0,4x – 1,5 = 0 | |||||||||||||||||
| Отделить корни уравнения f(x)=0 аналитически. Выполнить программную реализацию уточнения двух корней методом простых итераций с точностью ε=0,001. x3+ 0,2x2 + 0,5x – 1,2 = 0 | |||||||||||||||||
| Отделить корни уравнения f(x)=0 аналитически. Выполнить программную реализацию уточнения двух корней методом хорд с точностью ε=0,001. x3+ 0,4x2 + 0,6x – 1,6 = 0 | |||||||||||||||||
Отделить корни уравнения f(x)=0 графически. Выполнить программную реализацию уточнения одного корня методом половинного деления с точностью ε=0,001.
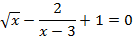
| |||||||||||||||||
Выполнить программную реализацию метода Гаусса для решения системы линейных уравнений с точностью до третьего знака после запятой:
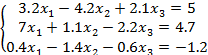
| |||||||||||||||||
Выполнить программную реализацию метода простой итерации для решения системы линейных уравнений с точностью до пятого знака после запятой:
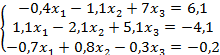
| |||||||||||||||||
Выполнить программную реализацию метода Зейделя для решения системы линейных уравнений с точностью до пятого знака после запятой:
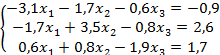
| |||||||||||||||||
Выполнить программную реализацию вычисления определенного интеграла по формуле правых прямоугольников разделив интервал интегрирования на 10 частей, оценить погрешность вычислений:
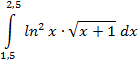
| |||||||||||||||||
Выполнить программную реализацию вычисления определенного интеграла по формуле трапеций разделив интервал интегрирования на 10 частей, оценить погрешность вычислений:
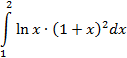
| |||||||||||||||||
Выполнить программную реализацию вычисления определенного интеграла по формуле Симпсона разделив интервал интегрирования на 10 частей, оценить погрешность вычислений:
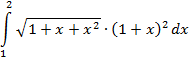
| |||||||||||||||||
Выполнить программную реализацию вычисления определенного интеграла по формуле средних прямоугольников с точностью ε=0,001.
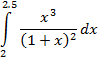
| |||||||||||||||||
Выполнить программную реализациюрешения задачи: для функции, заданной таблично в пяти узлах, найти значения ее первой и второй производных в первых 4-х узлах, используя формулы численного дифференцирования

| |||||||||||||||||
Выполнить программную реализацию вычисления определенного интеграла по формулам Ньютона-Котеса для функции, заданной таблично в пяти узлах:
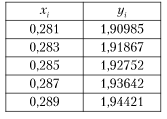
| |||||||||||||||||
Выполнить программную реализациюнахождения решения на отрезке 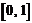 следующей задачи Коши: следующей задачи Коши: 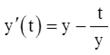 , , 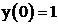 методом Эйлера для 10 точек. методом Эйлера для 10 точек.
| |||||||||||||||||
Выполнить программную реализациюрешения задачи:методом Рунге-Кутта четвертого порядка точности найти решение на отрезке  следующей задачи Коши следующей задачи Коши 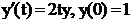 (взять 10 точек) (взять 10 точек)
| |||||||||||||||||
Выполнить программную реализацию решения задачи: заданы значения функции 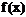 в узлах в узлах 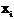 , получающиеся делением отрезка , получающиеся делением отрезка 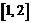 на 5 частей. Найти значения функции на 5 частей. Найти значения функции 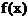 при при 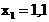 и и 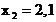 с помощью интерполяционных формул Ньютона. с помощью интерполяционных формул Ньютона.
| |||||||||||||||||
Выполнить программную реализацию вычисления определенного интеграла по формуле левых прямоугольников, разделив интервал интегрирования на 10 частей, оценить погрешность вычислений:
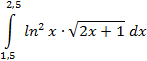
| |||||||||||||||||
Выполнить программную реализацию вычисления определенного интеграла по формуле Симпсона с точностью ε=0,001, определить фактическое число отрезков разбиения:

| |||||||||||||||||
Выполнить программную реализацию решения задачи: для функции, заданной таблично в пяти узлах, найти значение в точке x=0,3, используя интерполяционный многочлен Ньютона

| |||||||||||||||||
Выполнить программную реализацию метода простой итерации для решения системы линейных уравнений с точностью до третьего знака после запятой:
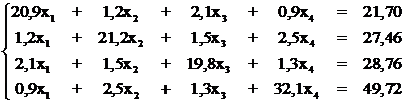
| |||||||||||||||||
Выполнить программную реализацию метода Зейделя для решения системы линейных уравнений с точностью до третьего знака после запятой:
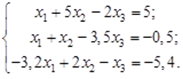
| |||||||||||||||||
Выполнить программную реализацию решения задачи: используя интерполяционный полином Ньютона, вычислить 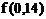 , где функция , где функция 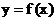 задана таблицей задана таблицей
| |||||||||||||||||
Выполнить программную реализацию нахождения корня уравнения методом половинного деления с точностью ε=0,0001:
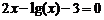
| |||||||||||||||||
Выполнить программную реализацию решения задачи:найти приближенные решения уравнения 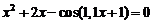 комбинированным методом с точностью комбинированным методом с точностью 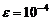 . .
| |||||||||||||||||
Выполнить программную реализациюрешения задачи интерполяции для функции, заданной таблично, используя метод Лагранжа для не равноотстоящих узлов.
Найти
|
 2017-12-14
2017-12-14 401
401
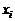
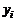
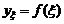 , при
, при 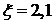 .
.






