Пример проявления закона сохранения в термодинамике

Опыты показывают, что термодинамические процессы невозможно обратить вспять. Примером тому может служить соприкосновение тел, имеющих различную температуру, при котором более нагретое будет отдавать тепло, а второе - принимать его. Обратный же процесс невозможен в принципе. Другим примером является переход газа из одной части сосуда в другую после открытия между ними перегородки, при условии что вторая часть пуста. Вещество в данном случае никогда не начнет движение в обратном направлении самопроизвольно. Из вышесказанного следует, что любая термодинамическая система стремится к состоянию покоя, при котором ее отдельные части находятся в равновесии и имеют одинаковую температуру и давление.

Гидродинамика

Применение закона сохранения в гидродинамических процессах выражается в принципе, описанном Бернулли. Он звучит так: сумма давления как кинестетической, так и потенциальной энергии на единицу объема одна и та же в любой отдельно взятой точке потока жидкости или газа. Это значит, что для измерения скорости потока достаточно измерить давление в двух точках. Делается это, как правило, манометром. Но закон Бернулли справедлив только в том случае, если рассматриваемая жидкость имеет вязкость, которая равна нулю. Для того чтобы описать течение реальных жидкостей, используется интеграл Бернулли, предполагающий добавление слагаемых, которые учитывают сопротивление.

Электродинамика

Во время электризации двух тел количество электронов в них остается неизменным, из-за чего положительный заряд одного тела равен по модулю отрицательному заряду другого. Таким образом, закон сохранения электрического заряда говорит о том, что в электрически изолированной системе сумма зарядов ее тел не изменяется. Это утверждение верно и тогда, когда заряженные частицы испытывают превращения. Таким образом, когда сталкиваются 2 нейтрально заряженные частицы, сумма их зарядов все равно остается равной нулю, так как вместе с отрицательно заряженной частицей появляется и положительно заряженная.

Заключение

·

·

·

·

·

 

Закон сохранения механической энергии, импульса и момента – фундаментальные физические законы, связанные с однородностью времени и его изотропностью. Они не ограничены рамками механики и применимы как к процессам, происходящим в космическом пространстве, так и к квантовым явлениям. Законы сохранения позволяют получать данные о различных механических процессах без их изучения при помощи уравнений движения. Если какой-то процесс в теории игнорирует данные принципы, то проводить опыты в таком случае бессмысленно, так как они будут нерезультативными.

Глава 2 Динамика материальной точки.

Динамика – раздел механики, в котором анализируются причины, определяющие характер того или иного движения. В основе динамики лежат три закона Ньютона.

Системы отсчёта, которые покоятся или движутся по отношению к удалённым звёздам с постоянной скоростью, называются инерциальными.

Любая система отсчёта, движущаяся относительно Земли прямолинейно и равномерно, тоже является инерциальной.

В инерциальной системе отсчёта пространство однородно и изотропно, а время однородно, так что законы физики в любом месте, при любой ориентации системы и во все моменты времени имеют один и тот же вид. Это утверждение называется принципом пространственно-временной симметрии.

На протяжении веков в науке господствовала классические представления о пространстве, времени и движении: пространство и время считались абсолютными, а фундаментальная скорость – бесконечно большой. Эти представления лежали в основе классической механики Ньютона и в концентрированном виде выражались преобразованиями Галилея. Наряду с поворотом, параллельным переносом в пространстве и сдвигом во времени они составляли группу симметрии классической механики (группу Галилея).

§ 2.3 Законы Ньютона. Сила. Масса. Импульс материальной точки

В первом законе Ньютона рассматривается тело, бесконечно удалённое от всех других тел и поэтому не испытывает внешнего воздействия. Такое тело называют изолированным

Первый закон Ньютона (закон инерции): любое тело сохраняет состояние относительного покоя или равномерного прямолинейного движения до тех пор, пока оно остаётся изолированным.

В соответствии с законом инерции изолированное тело способно находится лишь в одном из двух состояний: оно может либо покоиться, либо двигаться равномерно и прямолинейно, т.е. с постоянной скоростью υ. Объединяют эти два случая, то, что ускорение тела равно нулю. Поэтому первый закон Ньютона сводится к следующему утверждению: ускорение любой частицы убывает по мере удаления от неё окружающих тел. Строго говоря, изолированных тел в природе не существует, поэтому первый закон Ньютона описывает не реальную, а воображаемую ситуацию.

Тела, окружающие частицу, способны оказывать на неё определённое влияние, действие. Влияние тел (или частиц) на движение друг друга называют взаимодействием.

Мерой механического воздействия на тело других телявляется векторная физическая величина, называемая силой. Это воздействие проявляется в изменении скорости движущегося тела или изменении формы и размеров тела.

На вопрос о том, как движется тело под действием силы, отвечает второй закон Ньютона. Этот закон устанавливает связь между динамическими и кинематическими величинами и является основным законом динамики.

Второй закон Ньютона (уравнение движения): Ускорение, приобретаемое материальной точкой (телом) в инерциальной системе отсчета, пропорционально действующей на точку силе, обратно пропорционально массе материальной точки и по направлению совпадает с силой:

(2.5)

Взаимодействие тел является причиной их ускорения, а ускорение – следствием их взаимодействия. Чем больше сила, тем больше ускорение данного тела. А от направления силы зависит и направление приобретаемого телом ускорения.

Сила не единственная величина, от которой зависит ускорение. У каждой частицы есть своя (как говорят, внутренняя, т.е. не зависящая от состояния) величина, которую называют массой.

Масса m – скалярная физическая величина, являющаяся мерой инертности тела при поступательном движении

Инертность — свойство тела оказывать сопротивление при попытках привести его в движение или изменить величину или направление его скорости.

Чем больше масса тела, тем сильнее оно «сопротивляется» изменению его скорости.

С физической точки зрения предпочтительна несколько иная запись второго закона Ньютона. Воспользуемся формулой ускорения 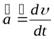и формулой (2.5) записанной в виде , тогда получаем:

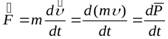(2.6)

где 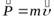– импульс материальной точки (старое название, до сих пор употребительное в теоретической механике — «количество движения»).

Используя понятие импульса, второй закон Ньютоном можно переписать в виде:

(2.7)

Изменение количества движения (импульса тела) пропорционально приложенной движущей силе и происходит по направлению прямой, по которой эта сила действует.

Формула (2.7) выражает второй закон Ньютона в более общей форме, т. е. когда масса движущегося тела конечных размеров изменяется с течением времени.

Если записать (2.7) в приближенной форме конечных малых приращений,

Δр = FΔt, (2.8)

то величина, стоящая в правой части, именуется импульсом силы за время Δt. В настоящее время этот термин употребляется редко.

Такая запись второго закона Ньютона более информативнее «школьной» формулы (2.5), потому что, решая дифференциальное уравнение (2.7), мы можем определить траекторию r(t) движения тела.

Третий закон Ньютона описывает ситуацию, когда во взаимодействии участвуют два тела.

Третий закон Ньютона (закон действия и противодействия): Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены в противоположные стороны вдоль соединяющих их прямой

(2.9)

Следует отметить, что сила F₁ это сила, с которой второе тело действует на первое, она приложена к первому телу. F₂ — сила, с которой первое тело действует на второе и приложена ко второму телу. Эти силы называют силами взаимодействия. Они направлены вдоль одной прямой и приложены к различным телам, поэтому эти силы не уравновешивают друг друга.

Первый и второй законы Ньютона справедливы только в инерциальных системах отсчёта. Третий закон Ньютона остаётся справедливым во всех (даже в неинерциальных) системах отсчёта. Например, сила притяжения Земли и Луны или сила взаимодействия двух неподвижных относительно друг друга точечных зарядов будет одной и той же независимо от того, из какой системы отсчёта (инерциальной или неинерциальной) мы наблюдаем за этими телами.

Следствия из законов Ньютона:

1. Сила является мерой воздействия, оказываемого на данную частицу со стороны других тел, и с увеличением расстояния до них убывает, стремясь к нулю.

2. Сила, с которой сразу несколько тел действуют на данную частицу, равна суме сил, с которой эти тела действуют на неё по отдельности (принцип независимости взаимодействия):

(2.10)

3. Сумма всех внутренних сил, действующих в любой системе, всегда равна нулю.

(2.11)

Внутренние силы не способны привести в движение систему тел как целое.

4. Отношение модулей ускорений, полученных двумя телами в результате взаимодействия друг с другом, равна обратному отношению их масс:

(2.12)

5. Масса системы тел равна сумме масс всех тел этой системы:

m_сист=m₁+m₂+m₃+…+ m_n(2.13)

Это свойство называется аддитивностью массы.

§2.4 Закон сохранения импульса

В результате взаимодействия тел их координаты и скорости могут непрерывно изменяться. Могут изменяться и силы, действующие между телами. К счастью, наряду с изменчивостью окружающего нас мира существует и неизменный фон, обусловленный так называемыми законами сохранения, утверждающими постоянство во времени некоторых физических величин, характеризующих систему взаимодействующих тел как целое.

Пусть на тело массой m в течение времени t действует какая-то постоянная сила . Выясним, как произведение этой силы на время её действия связано с изменением состояния этого тела.

Закон сохранения импульса обязан своим существованием такому фундаментальному свойству симметрии, как однородность пространства.

Из второго закона Ньютона (2.8) мы видим, что временная характеристика действия силы связана с изменением импульса Fdt=dP

Импульсом тела P называют произведение массы тела на скорость его движения:

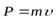(2.14)

Единица импульса — килограмм-метр в секунду (кг • м/с).

Направлен импульс всегда в туже сторону, что и скорость.

Всовременной формулировки закон сохранения импульса гласит: при любых процессах, происходящих в замкнутой системе, её полный импульс остаётся неизменным.

Докажем справедливость этого закона. Рассмотрим движение двух материальных точек, взаимодействующих только между собой (рис. 2.4).

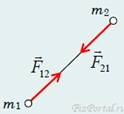  Такую систему можно назвать изолированной в том смысле, что нет взаимодействия с другими телами. По третьему закону Ньютона, силы, действующие на эти тела, равны по величине и противоположны по направлению:

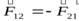
Рис.2.4

Используя второй закон Ньютона, это можно выразить как:

Объединяя эти выражения, получим

Перепишем данное соотношение, используя понятие импульса:

Следовательно,

или

Если изменение какой-либо величины равно нулю, то эта физическая величина сохраняется. Таким образом, приходим к выводу: сумма импульсов двух взаимодействующих изолированных точек остается постоянной, независимо от вида взаимодействия между ними.

(2.15)

Этот вывод можно обобщить на произвольную изолированную систему материальных точек, взаимодействующих между собой.   Если система не замкнута, т.е. сумма внешних сил, действующих на систему, не равна нулю: F ≠ 0, закон сохранения импульса не выполняется.

Центром масс (центром инерции) системы называют точку, координаты которой заданы уравнениями:

(2.16)

где х₁; у₁; z₁; х₂; у₂; z₂; …; х_N; у_N; z_N- координаты соответствующих материальных точек системы.

§2.5 Энергия. Механическая работа и мощность

Количественной мерой различных видов движения является энергия. При превращении одной формы движения в другую происходит изменение энергии. Точно также при передаче движения от одного тела к другому происходит уменьшение энергии одного тела и увеличение энергии другого тела. Такие переходы и превращения движения и, следовательно, энергии могут происходить либо в процессе работы, т.е. тогда, когда осуществляется перемещение тела при воздействии силы, либо в процессе теплообмена.

Для определения работы силы F рассмотрим криволинейную траекторию (рис. 2.5), по которой движется материальная точка из положения 1 в положение 2. Разобьем траекторию на элементарные, достаточно малые перемещения dr; этот вектор совпадает с направлением движения материаль ной точки. Модуль элементарного перемещения обозначим dS: |dr| = dS. Так как элементарное перемещение достаточно мало, то в этом случае силу F можно рассматривать неизменной и элементарную работу вычислять по формуле работы постоянной силы:

dA = F соsα dS = F соsα|dr|, (2.17)

или как скалярное произведение векторов:

(2.18)

Э лементарнаяработа или просто работа силы, есть скалярное произведение векторов силы и элементарного перемещения.

Суммируя все элементарные работы, можно определить работу переменной силы на участке траектории от точки 1 до точки 2 (см. рис. 2.5). Эта задача сводится к нахождению следующего интеграла:

(2.19)

Пусть эта зависимость представлена графически (рис.2.6), тогда искомая работа определяется на графике площадью заштрихованной фигуры.

Заметим, что в отличие от второго закона Ньютона в выражениях (2.22) и (2.23) под F совсем не обязательно понимать равнодействующую всех сил, это может быть одна сила или равнодействующая нескольких сил.

Работа может быть положительной или отрицательной. Знак элементарной работы зависит от значения соsα. Так, например, из рисунка 2.7 видно, что при перемещении по горизонтальной поверхности тела, на которое действуют силы F, F_тр и mg, работа силы F положительна (α> 0), работа силы трения F_тр отрицательна (α = 180°), а работа силы тяжести mg равна нулю (α = 90°). Так как тангенциальная составляющая силы F_t = F соs α, то элементарная работа вычисляется как произведение F_t на модуль элементарного перемещения dS:

dA = F_tdS (2.20)

Таким образом, работу совершает лишь тангенциальная составляющая силы, нор­мальная составляющая силы (α = 90°) работы не совершает.

Быстроту совершения работы характеризуют величиной, называемой мощностью.

Мощностью называется скалярная физическая величина, равная отношению работы ко времени, за которое она совершается:

(2.21)

Учитывая (2.22), получаем

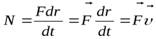(2.22)

или N = Fυcosα (2.23) Мощность равна скалярному произведению векторов силы и скорости.

Из полученной формулы видно, что при постоянной мощности двигателя сила тяги больше тогда, когда скорость движения меньше . Именно поэтому водитель автомобиля при подъёме в гору, когда нужна наибольшая сила тяги, переключает двигатель на малую скорость.

§2.6 Кинетическая энергия

С понятием работы тесно связано другое фундаментальное физическое понятие – понятие энергии. Поскольку в механике изучается, во-первых, движение тел, а во-вторых, взаимодействие тел между собой, то принято различать два вида механической энергии: кинетическую энергию, обусловленную движением тела, и потенциальную энергию, обусловленную взаимодействием тела с другими телами.

Кинетической энергией механической системы называют энергию, зависящую от скоростей движения точек этой системы.

Выражение для кинетической энергии можно найти, определив работу равнодействующей силы, приложенной к материальной точке. На основании (2.24) запишем формулу для элементарной работы равнодействующей силы:

(2.24)

Так как , то dА = mυdυ. (2.25)

Чтобы найти работу равнодействующей силы при изменении скорости тела от υ₁ до υ₂ проинтегрируем выражение (2.29):

(2.26)

Так как работа — мера передачи энергии от одного тела другому, то на

основании (2.30) запишем, что величина есть кинетическая энергия

тела: 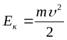откуда вместо (1.44) получаем

(2.27)

Теорему, выраженную формулой (2.30) принято называть теоремой о кинетической энергии. В соответствии с ней работа сил, действующих на тело (или систему тел), равна изменению кинетической энергии этого тела (или системы тел).

Из теоремы о кинетической энергии следует физический смысл кинетической энергии: кинетическая энергия тела равна работе, которую оно способно совершать в процессе уменьшения своей скорости до нуля. Чем больше «запас» кинетической энергии у тела, тем большую работу оно способно совершить.

Кинетическая энергия системы равна сумме кинетических энергий материальных точек, из которых эта система состоит:

(2.28)

Если работа всех сил, действующих на тело, положительна, то кинетическая энергия тела возрастает, если работа отрицательна, то кинетическая энергия убывает.

Очевидно, что элементарная работа равнодействующей всех приложенных к телу сил будет равна элементарному изменению кинетической энергии тела:

dА = dЕ_к. (2.29)

В заключение заметим, что кинетическая энергия, как и скорость движения, имеет относительный характер. Например, кинетическая энергия пассажира, сидящего в поезде, будет разной, если рассматривать движение относительно полотна дороги или относительно вагона.

§2.7 Потенциальная энергия

Вторым видом механической энергии является потенциальная энергия – энергия, обусловленная взаимодействием тел.

Потенциальная энергия характеризует не любое взаимодействие тел, а лишь такое, которое описывается силами, не зависящими от скорости. Большинство сил (сила тяжести, сила упругости, гравитационные силы и т.д.) именно таковы; исключением являются лишь силы трения. Работа рассматриваемых сил не зависит от формы траектории, а определяется лишь её начальным и конечным положением. Работа таких сил на замкнутой траектории равна нулю.

Силы, работа которых не зависит от формы траектории, а зависит лишь от начального и конечного положения материальной точки (тела) называют потенциальными или консервативными силами.

Если тело взаимодействует со своим окружением посредством потенциальных сил, то для характеристики этого взаимодействия можно ввести понятие потенциальной энергии.

П отенциальной называют энергию, обусловленную взаимодействием тел и зави­сящую от их взаимного расположения.

Найдем потенциальную энергию тела, поднятого над землей. Пусть тело массой m равномерно перемещается в гравитационном поле из положения 1 в положение 2 по поверхности, сечение которой плоскостью чертежа показано на рис. 2.8. Это сечение является траекторией материальной точки (тела). Если трение отсутствует, то на точку дейст­вуют три силы:

1) сила N со стороны поверхности нормально поверхности, работа этой силы равна нулю;

2) сила тяжести mg, работа этой силы А₁₂;

3) сила тяги F со стороны некоторого движущего тела (двигатель внутреннего сгорания, электродвигатель, человек и т. п.); работу этой силы обозначим А_T.

Р ассмотрим работу силы тяжести при перемещении тела вдоль наклонной плоскости длиной ℓ (рис. 2.9). Как видно из этого рисунка, работа равна

А' = mgℓ соsα = mgℓ соs(90° + α) = - mgℓ sinα

Из треугольника ВСD имеем ℓ sinα = h, по­этому из последней формулы следует:

А' = -mgh.

Траекторию движения тела (см. рис. 2.8) можно схематично представить небольшими участками наклонной плоскости, поэтому для, работы силы тяжести на всей траектории 1 -2 справедливо выражение

A₁₂=mg (h₁-h₂) =-(mg h₂ - mg h₁) (2.30)

Итак, работа силы тяжести не зависит от траектории тела, а зависит от различия в высотах расположения начальной и конечной точек траектории.

Величину

е_п = mg h (2.31)

называют потенциальной энергией материальной точки (тела) массой m поднятой над землей на высоту h. Следовательно, формулу (2.30) можно переписать так:

A₁₂= =-(En₂- En₁) или A₁₂= =-ΔEn (2.32)

Работа силы тяжести равна взятому с обратным знаком изменению потенциальной энергии тел, т. е. разности ее конечного и начального значений (теорема о потенциальной энергии).

Подобные рассуждения можно привести и для упруго деформированного тела.

(2.33)

Отметим, что физический смысл имеет разность потенциальных энергий как величина, определяющая работу консервативных сил. В связи с этим безразлично, какому положению, конфигурации, следует приписать нулевую потенциальную энергию.

Из теоремы о потенциальной энергии можно получить одно очень важное следствие: консервативные силы всегда направлены в сторону уменьшения потенциальной энергии. Установленная закономерность проявляется в том, что любая система, предоставленная самой себе, всегда стремится перейти в такое состояние, в котором её потенциальная энергия имеет наименьшее значение. В этом заключается принцип минимума потенциальной энергии.

Если система в данном состоянии не обладает минимальной потенциальной энергией, то это состояние называют энергетически невыгодным.

Если шарик находится на дне вогнутой чаши (рис.2.10,а), где его потенциальная энергия минимальна (по сравнению с ее значениями в соседних положениях), то его состояние более выгодно. Равновесие шарика в этом случае является устойчивым: если сместить шарик в сторону и отпустить, то он снова возвратится в своё первоначальное положение.

Энергетически невыгодным, например, является положение шарика на вершине выпуклой поверхности (рис.2.10, б). Сумма сил, действующих при этом на шарик, равна нулю, и потому, этот шарик будет находится в равновесии. Однако равновесие это является неустойчивым: достаточно малейшего воздействия, чтобы он скатился вниз и тем самым перешёл в состояние энергетически более выгодное, т.е. обладающее меньшей

п отенциальной энергией.

При безразличном равновесии (рис. 2.10, в) потенциальная энергия тела равна потенциальной энергии всех его возможных ближайших состояний.

На рисунке 2.11 можно указать некоторую ограниченную область пространства (напримерcd), в которой потенциальная энергия меньше, чем вне её. Эта область получила название потенциальной ямы.

§2.8 Закон сохранения энергии в механике

В 1018 г.ЭммиНётер, немецкий физик и математик, доказал фундаментальную теорему физики, которую в упрощённом виде можно сформулировать так: каждому свойству симметрии пространства и времени соответствует свой закон сохранения. В частности, как следует из теоремы (теоремы Нётер) однородности времени должен соответствовать закон сохранения энергии: при любых процессах, происходящих в замкнутой консервативной системе, её полная механическая энергия не изменяется.

Элементарная работа потенциальных сил равна взятому с обратным знаком эле­ментарному изменению потенциальной энергии dA= -dE_п. Так как иных сил в системе нет, то та же элементарная работа равна элементарному изменению кинетической энергии dA= dE_к. По­этому можем записать

-dE_п = dE_к

dE_к + dE_п = 0,

d(Е_к + Е_п) = 0. (2.34) Обозначим

Е_к + Е_п = Е (2.35)

здесь Е — полная механическая энергия. Из (2.39) видим, что полная механическая энергия остается постоянной:

E=const (2.36)

При решении задач в механике удобно пользоваться законом сохранения энергии в виде

ΔE_к = ΔE_п или Е_к1 + Е_п1 = Е_к2 + Е_п2. (2.37) здесь Е_к1 и Е_п1, — соответственно кинетическая и потенциальная энергии тела (системы) в начальном положении; Е_к2 и Е_п2 — то же для конечного положения тела (системы).

Закон сохранения энергии в механике является частным случаем более общего закона сохранения и превращения энергии, который является одним из основных законов природы.

В земных условиях невозможно указать консервативную систему, хотя бы потому, что всегда действуют силы трения и сопротивления (диссипативные силы), происходит уменьшение механической энергии (диссипация энергии). В этом случае механическая энергия уже не будет оставаться постоянной; она будет изменяться, и её изменение, как это видно из формулы (2.38) будет складываться из изменения кинетической энергии ΔE_к, и изменения потенциальной энергии ΔE_п:

ΔЕ= ΔE_к,+ ΔE_п.. (2.38)

Учитывая соотношения (2.27) и (2.32), выражающие теорему о кинетической и потенциальной энергиях, последнее равенство можно переписать так:

ΔЕ= А_пот+А_дис-А_пот= А_дис. (2.39)

Изменение полной механической энергии неконсервативной системы равно сумме работы диссипативных сил.

Так как диссипативные силы направлены противоположно перемещению, то работа этих сил отрицательна и, следовательно, механическая энергия системы уменьшается.

§2.9 Столкновение тел

Столкновение тел – одно из наиболее часто встречающихся явлений в жизни. При столкновении происходит их кратковременное взаимодействие, сопровождающееся как деформацией, так и изменением направления их движения. Особый интерес представляют два вида столкновений – абсолютно упругий и абсолютно неупругий удары.

Простейшим видом соударения является центральный удар тел. При этом ударе тела движутся только поступательно, их скорость направлена по прямой, соединяющей центры масс.

Абсолютно неупругий удар. Так называется столкновение двух тел, в результате которого они соединяются вместе и движутся дальше как одно целое. Например, столкновение слипающихся пластилиновых шариков; попадание ружейной пули в ящик с песком и т.д.

П усть один из шаров массойm₁ догоняет другой массой m₂ (рис. 2.12).

Можно записать

m₁υ₁+m₂υ₂=(m₁+m₂)υ (2.40)

откуда (2.41)

здесь υ₁ и υ₂ — скорости взаимодействующих шаров до удара; υ — их скорость после удара.

Направления векторов скоростей в общем случае определяются правилом: скорости положительны, если направлены вдоль оси ОХ, и отрицательны, если направлены противоположно.

Рассмотрим несколько частных случаев.

1. Если массы шаров равны (m₁ = m₂), то из (2.45) получим

(2.42)

2. Удар шара о стенку. Неподвижное тело (стенка) (υ₂ = 0) значительно массивнее шара (m₂» m₁), тогда

(2.43)

т.е. налетевшее тело остановится после абсолютно неупругого удара, при этом υ₂ считаем не слишком большой.

При абсолютно неупругом ударе механическая энергия шаров не сохраняется, так как в системе действуют диссипативные силы и происходит потеря кинетической энергии, в результате чего механическая энергия системы уменьшается, переходя во внутреннюю энергию ΔЕ сталкивающихся тел (которые при этом нагреваются). Но закон сохранения полной энергии выполняется, т.е. сумма всех видов энергии замкнутой системы тел до и после столкновений остаётся неизменной:

(2.44)

Абсолютно упругий удар. Так называется столкновение тел, в результате которого не происходит соединения тел в одно целое и их внутренние энергии остаются неизменными. При абсолютно упругом ударе сохраняется не только импульс, но и механическая энергия системы.

К абсолютно упругому удару можно применить закон сохранения механической энергии:

(2.45)

где m₁ и m₂ — массы взаимодействующих шаров; υ₁, υ₂ – их скорости до удара; u₁, u₂— после удара.

По тем же причинам, которые были изложены для абсолютно неупругого удара, к этому случаю можно применить и закон сохранения импульса:

m₁υ₁+ m₂υ₂ = m₁ u₁+ m₂ u₂ (2.46)

Решая совместно уравнения (2.49) и (2.50), получим

(2.47)

(2.48)

Примеры решения задач

Пример 2.1. В вагоне, движущемся горизонтально с ускорением 2м/с², висит на шнуре груз массой 200г. найти силу натяжения шнура и угол отклонения его от вертикали.

Решение:

На груз независимо от состояния движения действуют две силы: сила тяжести и сила натяжения (рис.2.16).

В покоящемся или равномерно движущемся вагоне обе силы коллинеарные и их векторная сумма равна нулю. При движении вагона в системе координат, связанной с Землёй, второй закон Ньютона (для груза) имеет вид

В проекциях

m a _x=m a =Tsinαm a _y=0= Tcosα-mg

решаем систему уравнений

разделив первое уравнение на второе, получим , откуда

Возведя оба уравнения системы в квадрат, определим силу натяжения нити:

Пример 2. 2. Невесомый блок укреплен в вершине наклонной плоскости, составляющей с горизонтом угол а =30°. Гири 1 и 2 одинаковой массы m₁ = m₂ = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т, если коэффициент трения гири 2 о наклонную плоскость μ= 0,1. Трением в блоке пренебречь.

Решение

П усть m₁ =m₂ = m. Запишем уравнение второго закона Ньютона для первой и второй гири в проекциях на направление их движения с учетом T₁ =T₂ = T

Получим:

m₁ а = m₁g - T (1)

m₂ а = T-m₂g sina - F_тр (2) 0 = N - m₁g cosa (3)

Из уравнения (3) следует, что N = m₁g cosa. А так как F_тр= m N, то

F_тр= m m₁g cosa.

Подставив это выражение в уравнение (2), получим:

m₁ а = m₁g - T (4)

m₂ а = T-m₂g sina - m m₁g cosa (5)

Сложим левые и правые части уравнений (4) и (5)

(m₁+ m₂ ) а = m₁ g – m₂g (sina + m cosa)

Отсюда

.

Пример 2.3. На покоящуюся частицу массой m в момент t = 0 начала действовать сила F= a t(τ-t), где a – постоянная, τ - время действия силы. Найти путь, пройденный телом за время действия силы.

Решение

Запишем уравнение движения тела

Отсюда

Постоянная интегрирования равна нулю

Пример 2.4. На небольшое тело массы m, лежащее на гладкой горизонтальной плоскости в момент t = 0 начала действовать сила, зависящая от времени по закону F=at, где a - постоянная. Направление этой силы всё время составляет угол α с горизонтом (рис.2.18). Найти скорость тела в момент отрыва от плоскости.

Р ешение

Уравнение движения тела имеет вид

В проекциях на направление движения (ось 0Х)

Отсюда скорость тела в момент отрыва запишем в виде

где τ- момент отрыва тела от горизонтальной поверхности.

Отрыв тела наступает в момент, когда сумма проекций сил, действующих на него, на ось У станет равной нулю, т.е.

Отсюда находим момент времени, когда происходит отрыв

Скорость в момент отрыва будет равна: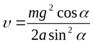

Пример 2.5. Тело массой 1кг под действием постоянной силы движется прямолинейно. Зависимость пути, пройденного телом, от времени задана уравнением S=2t²+4t+1. Определите: а) работу силы за 10с с начала её действия; 2) зависимость кинетической энергии от времени.

Решение

Работа, совершаемая силой, выражается через криволинейный интеграл:

(1)

Сила, действующая на тело, по второму закону Ньютона равна

F=m a или (2)

Мгновенное значение ускорения определяется первой производной от скорости по времени или второй производной от пути по времени. В соответствии с этим находим

(3)

(4)

Тогда

(5)

Из выражения (3) определим

dS=(4t+4)dt (6)

Подставим (5) и (6) в уравнение (1), получим

По этой формуле определим работу, совершаемую силой за 10с

Кинетическая определяется по формуле

Ответ: А=960Дж; Т=m(8t²+16t+8)

Пример 2.6. Самолет Ил-62 имеет четыре двигателя, сила тяги каждого 103 кН.Какова полезная мощность двигателей при полете самолета со скоростью 864 км/ч?

Решение

Механическая работа при совпадении направлений вектора силы и перемещении равна

A = Fs.

Отсюда для механической мощности имеем

.

Так как при равномерном прямолинейном движении

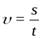, то N = Fυ;

N = 240 м/с × 1,03 × 10⁵ Н» 2,5 × 10⁷ Вт = 25 000 кВт.

Пример 2.7. На частицу, движущуюся горизонтально, действует сила которая зависит от пройденного пути как . Найти работу, которую совершила эта сила на участке от 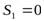до .

Решение

В данном случае F является величиной переменной, зависящей от пути. Работу этой силы найдём как

Пример 2.8. Потенциальная энергия растянутой пружины имеет вид

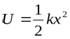. Найти силу, с которой пружина действует на руку.

Решение

Сила упругости является консервативной силой. Направим ось Х вдоль оси пружины. Тогда . Знак минус указывает на то, что сила F направлена в сторону, противоположную смещению, т.е. является силой притяжения.

Пример 2.9. Потенциальная энергия частицы в некотором двумерном силовом поле имеет вид U= αx²+βy², где α и β - положительные постоянные. Какую форму имеет поверхность, для которой модуль вектора силы F = const.

Решение

Используя связь между силой и энергией в виде (1.20), находим проекции силы

F_x=-2αx; F_y=-2βy

Модуль силы

Найдём поверхность, для которой F = const

Поверхность, для которой F = const, имеет форму эллипса.

Пример 2.10. Вычислите работу силы упругости при изменении деформации пружины жесткостью 200 Н/м от х₁ = 2 см до х₂ = 6 см.

Решение

По закону Гука, проекция вектора силы упругости на ось ОХ, направленную по вектору перемещения конца пружины при ее деформации, равна

(F_упр)_x = -kx.

Так как сила упругости изменяется пропорционально деформации, то для вычисления работы можно найти среднее значение ее проекции при изменении деформации пружины от 2 до 6 см:

;

= - 8 Н.

Работа силы упругости равна произведению модуля среднего значения силы на модуль перемещения и косинус угла между этими векторами:

A = F_{упр. ср}(x₂ – x₁) cos a.

При растяжении пружины вектор силы упругости направлен противоположно вектору перемещения, поэтому угол a между ними равен 180°, а cosa = -1. Тогда работа силы упругости будет равна

А = 8 Н × 4 × 10^-2 м × (-1) = -0,32 Дж.

Работа силы упругости может быть найдена и по изменению потенциальной энергии пружины:

;

= - 0,32 Дж.

Пример 2.11. Горизонтально катящийся шар m массой испытывает абсолютно неупругое столкновение с таким же неподвижным шаром. Найти уменьшение кинетической энергии системы. Скорость первого шара до удара υ. Энергию вращения шаров не учитывать.

Решение

Система (шар+шар) является замкнутой и поэтому при решении можно воспользоваться законом сохранения импульса. Импульс системы до удара Р₁= m·υ, после удара Р₂ = 2 m·υ₂, где υ₂ - скорость движения шаров (удар абсолютно неупругий, следовательно, после удара шары движутся вместе). Итак,

m·υ= 2 m·υ₂

Отсюда находим скорость шаров после удара . Уменьшение кинетической энергии найдём как разность начальной и конечной кинетической энергии найдём как разность начальной и конечной кинетической энергии системы

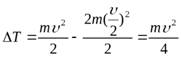
Пример 2.12. Пуля, массой m₁ = 10 г, летящая горизонтально, абсолютно упруго соударяется с шаром массой m₂ = 6 кг, подвешенным на легком стержне длиной l = 1 м, и отскакивает в противоположном направлении. В результате удара шар отклоняется от вертикали на угол α = 40°. Найти скорость пули до и после удара. Массой стержня пренебречь.

Р ешение

В горизонтальном направлении на пулю и шар внешние силы не действуют, поэтому сумма проекций импульсов пули и шара на ось Ох (рис. 16, а) остается постоянной:

m₁υ₁ = - m₁ и ₁ + m₂ и ₂ (1)

где и ₁, и ₂ – модули скоростей соответственно пули и шара после удара.

Поскольку удар абсолютно упругий, то суммарная механическая энергия пули и шара сохраняется:

(2)

На основании закона сохранения энергии имеем: ,

где h - высота, на которую поднялся шар.

Как видно из рис. 16 h = ℓ- ℓ cos α = ℓ (1 - cos α). Подставив это выражение в последнее уравнение, получим:

. (3)

Нами получена система трех уравнений с тpемя неизвестными υ₁, и ₁, и ₂. Для решения этой системы удобно переписать уравнения (1.21) и (1.22) так:

m₁(υ₁ + u ₁) = m₂ u ₂ (4)

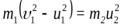(5)

Разделив теперь почленно уравнение (1.25) на уравнение (1.24), получим:

υ₁ – u ₁ = u ₂. (6)

Умножив обе части этого уравнения на m₁ и после этого сложив его почленно с уравнением (1.21), получим: 2m₁υ₁ = u ₂(m₁ + m₂), откуда ,

или, учитывая выражение (1.23),

. (7)

На основании уравнений (1.23), (1.26) и (1.27) получим:

. (8)

Подставив в формулы (1.27) и (1.28) числовые значения величин и произведя вычисления, получим: υ₁ = 631 м/с, и ₁ = 629 м/с.

Пример 1.26. Атомное ядро с массой m и кинетической энергией T сталкивается с другим ядром, которое до столкновения покоилось. Происходит ядерная реакция, в результате которой образуются две частицы с массами m₁ и m₂, причём на реакцию затрачивается энергия Q. При каких условиях скорости образовавшихся частиц будут направлены вдоль скорости падающей частицы.

Решение

Пусть Р - импульс падающей частицы, Р₁ и Р₂ –импульсы образовавшихся частиц. Если все импульсы имеют одинаковое направление, то

Р = Р₁ + Р₂ . Кроме того,

Учитывая, что , исключаем из полученных уравнений Р₂и получаем квадратное уравнение относительно Р₁. Из условия вещественности корней получаем искомое условие

.

79. Пушка массы М стоит на гладкой горизонтальной поверхности и в момент t = 0 выстреливает снарядом массы m под углом a к горизонту, при этом снаряд вылетает со скоростью υ₀. Найти, какую скорость приобретает пушка после выстрела.

Решение:

На систему пушка – снаряд действуют две внешние силы: сила тяжести и сила реакции опоры со стороны горизонтальной поверхности. Обе силы направлены по вертикали. Система не замкнута – писать закон сохранения импульса в векторном виде нельзя. Однако, так как проекция внешних сил на горизонталь равна нулю, можно записать закон сохранения импульса только для его проекции на это направление, то есть на ось Ох:

0 = - М и + m υ ₀cosa.

Из последнего соотношения легко находится скорость пушки

и = .

83. Найти скорость вылета снаряда из пружинного пистолета массой m при выстреле вертикально вверх, если жесткость пружины равна k, а сжатие равно х.

Решение

Сжатая пружина обладает потенциальной энергией, которая расхордуется на совершение работы по преодолению силы тяжести снаряда и сообщению ему кинетической энергии. Потенциальная энергия пружины равна работе переменной силы упругости на перемещении х:

F_упр = -kx; ;

;

;

.