Вопрос 15 Аксиоматический метод в математике. Общая характеристика аксиоматического метода

В математике АКСИОМАТИЧЕСКИЙ МЕТОД зародился в работах древнегреческих геометров. Блестящим, остававшимся единственным вплоть до ХIХ века образцом применения АКСИОМАТИЧЕСКОГО МЕТОДА была геометрическая система, известная под названием «НАЧАЛ» ЕВКЛИДА (около 300 лет до новой эры)

Среди аксиом Евклида была так называемая «аксиома о параллельных прямых» (она же — «пятый постулат Евклида»). Сегодня она формулируется так: «Через точку, не лежащую на данной прямой, можно провести ровно одну прямую, параллельную данной» (у Евклида была несколько иная формулировка, но эквивалентная этой, как показали более поздние ученые).

По своему характеру эта аксиома сильно отличалась от остальных его аксиом, была сложнее их. Многие математики в течение почти двух тысяч лет предпринимали попытки доказать этот постулат, исходя из остальных аксиом. И лишь в 19 веке было окончательно выяснено (и в чем состоял выдающийся вклад русского математика Николая Лобачевского), что данную аксиому нельзя вывести из остальных аксиом геометрии.

Наконец, на рубеже 19–20 веков немецкий математик Давид Гильберт, во-первых, записал евклидову геометрию в виде формальной аксиоматической теории (дописав, в том числе, некоторые недостающие аксиомы), а во-вторых, показал, что эта теория полна, то есть всякое утверждение можно в данной теории либо доказать, либо опровергнуть (то есть доказать его

отрицание). Это было одним из величайших вкладов в развитие аксиоматического метода и подтолкнуло к последовавшей формализации всей математики.

Аксиоматический метод — это способ построения и систематизации научного знания в форме так называемых аксиоматических теорий, при котором некоторые утверждения выбираются в качестве исходных положений (аксиом), а все остальные утверждения (теоремы) этой теории доказывают (или выводят), исходя лишь из аксиом с помощью чисто логических рассуждений.

И аксиомы, и теоремы — это высказывания (утверждения) на некотором языке о некоторых понятиях (или терминах). Поэтому, прежде чем формулировать аксиомы и доказывать теоремы, мы должны договориться, о каких именно понятиях пойдет речь. Понятия делятся на два вида: одни обозначают объекты, которыми занимается теория, другие

обозначают отношения между ними.

Одни понятия можно определять через другие. В какой-то момент необходимо остановиться и объявить некоторые понятия неопределяемыми (или исходными), и через них определять все остальные понятия (определяемые или производные), о которых говорится в данной теории.

Итак, чтобы пользоваться аксиоматическим методом построения теории, нужно:

(1) выбрать исходные понятия;

(2) сформулировать аксиомы («исходные» утверждения) об этих понятиях;

(3) выводить новые утверждения (теоремы) о них, пользуясь логикой и аксиомами.

В пунктах (2) и (3) можно вводить новые понятия (определяемые) через исходные и определенные ранее. Ввод новых понятий не добавляет новой информации, так как всегда можно заменить употребление этих понятий на их определение через исходные. Однако их использование позволяет сделать формулировки утверждений и доказательств короче и понятней. При этом надо следить, чтобы понятия вводились «последовательно» — каждое «следующее» новое понятие определялось через «ранее» определенные, то есть чтобы не возникал «порочный круг» (одно понятие определяется через второе, второе — через третье, и т.д., последнее — через первое).

Аналогично, в пункте (3) можно опираться не только на выбранные аксиомы, но и на доказанные «ранее» теоремы. Это позволяет делать доказательства более краткими, не доказывая одни и те же утверждения повторно.

 

 

Вопрос 16содержательная и полуформаьная аксиоматические теории

Аксиоматический метод применяется не на этапе нового знания, а на этапе систематизации уже добытого знания. Аксиоматический метод можно образно представить как метод «шлифовки» уже добытого, но еще не оформленного, не систематизированного достаточно полно знания. Однако это только одна сторона дела. В результате «шлифовки», т.е. применения аксиоматического метода, теория приобретает логическую завершенность и такую форму, которая необходимо ведет к поиску нового зна-ния, выводит на конструирование новых математических теорий. Соответствующая функция аксиоматизации проявляется не сразу, так как она сама как метод формализации тоже развивается, т.е. аксиоматизация выступает в двух аспектах: и как результат формализации и как средство познания

 

Как полуформальная, так и формальная аксиоматизация в качестве предмета изучения использует интерпретацию. Метод интерпретации позволяет выработать способы истолкования, определения исходных понятий одной системы средствами другой, уже известной системы. Интерпретация как метод познания действительности применялся математикой давно. При интерпретации первоначальных объектов математики происходит соотнесение их с реальными объектами, благодаря чему знание о них становится более содержательным. Однако такая соотнесенность имеет опосредованный характер и ограниченное число интерпретаций, вплоть до единичной, что связано со спецификой объектов определенной конкретной области. При интерпретации более высоких уровней абстрактных объектов, образующих уже систему формализованную, возможна целая совокупность, множество интерпретаций, среди которых выделяются математические и естественнонаучные. Одни математические структуры интерпретируются другими математическими структурами.

Для формальной теории истинность теоремы означает, прежде всего, её доказуемость. Для содержательной теории утверждение истинно, если оно истинно в любой модели данной теории. Таким образом, и для любой формальной теории возникают a’ priori два понимания “истинности” формулы: доказуемость и тождественная истинность (истинность при любой интерпретации рассматриваемой теории).

Интерпретация формальной теории (или модель теории)определяется понятию интерпретации для множества формул исчисления предикатов. Не вдаваясь в формальности, ограничимся только намёком: модель теории (или интерпретация) – это некоторое множество вместе с зафиксированными на нём конкретными константами, предикатами и функциями для всех выделенных константных, предикатных и функциональных символов, участвующих в аксиомах теории. При этом требуется, чтобы все аксиомы теории в любой интерпретации этой теории представляли собой истинные в этой модели утверждения.

 

 

 

17. Метод интерпретации. Формальная аксиоматическая теория.

Интерпретация в математике, логике — совокупность значений (смыслов), придаваемых тем или иным способом элементам (выражениям, формулам, символам и т. д.) какой-либо естественнонаучной или абстрактно-дедуктивной теории. В тех же случаях, когда такому «осмыслению» подвергаются сами элементы этой теории, то говорят также об интерпретации символов, формул и т. д.

Конец XIX – начало XX вв.

Стремление к формальному построению аксиоматических теорий;

Поиск новых средств и методов обоснования математики в связи с парадоксами теории множеств;

Понимание того, что метод доказательства с помощью моделей и интерпретаций имеет лишь относительный характер (аксиоматика Пеано, непротиворечивость арифметики целых чисел)

Вариант формализованной аксиоматики осуществляется путем замены содержательных исходных положений (аксиом) и исходных объектов формулами и символами.

Знаки и формулы этого языка не несут никакого содержательного смысла.

Вывод: Математическая теория, непротиворечивость которой требовалось доказать, стала предметом другой математической теории, которую Гильберт назвал математикой или теорией доказательств.

К. Гёдель – математик и логик.

Выводы из теории Гёделя:

Любая формула, отношение которой невыводимо, является выполнимой;

Непротиворечивость формализованной системы ведет к ее неполноте.

Любая процедура доказательства истинных утверждений элементарной теории чисел заведомо неполна. Для любых систем доказательств существуют истинные утверждения, которые даже в таком определенном направлении математики остаются недоказуемыми.

Гёдель делает вывод об ограниченности аксиоматического метода.

 

18. История возникновения фрактальной геометрии. Значение фрактальной геометрии.

Понятие фрактал, появилось в конце 70-х годов 20 в.. Оно было введено в обращение в 1975 году французским математиком польского происхождения Бенуа Мандельбротом для обозначения нерегулярных, но самоподобных структур, которыми он занимался.

Важную роль в широком распространении идей фрактальной геометрии сыграла книга Б. Мандельброта «Фрактальная геометрия природы». В работах Б. Мандельброта использованы научные результаты, полученные многими учеными. Это объясняется тем, что самому факту появления фракталов более ста лет. Однако появление их в математической литературе было встречено с неприязнью. Общее мнение признало их патологией, представляющей интерес только для исследователей математических причуд, а не для подлинных ученых. Заслуга Б. Мандельброта в том, что ему удалось собрать разрозненные сведения, объединить их в единую систему, увидеть общее в многообразии, указать на важность своего открытия.

История развития идей фрактальной геометрии тесно связана с именами таких известных математиков, как К. Вейерштрасс, Г. Кантор, Дж. Пеано, Ф. Хаусдорф, А.С. Безикович, Х. Кох, В. Серпинский и др. Так К. Вейерштрасс впервые ввел в обращение непрерывную, но нигде не дифференцированную функцию. Ф. Хаусдорф в 1919 г. ввел понятие о дробной размерности множеств и привел примеры таких множеств. Среди них были канторовское множество, кривая Коха и другие математические объекты. Идеи Ф. Хаусдорфа впоследствии были существенно развиты А.С. Безиковичем.

Большой вклад в будущую фрактальную геометрию внесли работы французских математиков Г. Жулиа и П. Фату, которые в начале ХХ века занимались теорией рациональных отображений в комплексной плоскости. Практически полностью забытая, их деятельность получила неожиданное развитие в начале восьмидесятых годов, когда с помощью компьютеров математикам удалось получить прекрасные картины, показывающие примеры таких отображений.

В настоящее время язык фрактальной геометрии широко используется

в физике:

– при изучении поглощения или рассеяния излучения в пористых средах;

– для характеристики сильно развитой турбулентности;

– при моделировании свойств поверхности твердых тел;

– для описания диэлектрического пробоя и молнии;

– при анализе процессов усталостного разрушения материалов;

– при исследовании различных стадий роста вещества за счет диффузии;

в астрономии:

– при описании процессов кластеризации галактик во Вселенной;

в картографии:

– при изучении форм береговых линий и разветвленной сети речных русел;

в биологии:

– при анализе строения кровеносной системы или рассмотрении сложных поверхностей клеточных мембран.

 

 

Вопрос 19 Геометрические фракталы: триадная кривая Кох.

Геометрические фракталы самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.

Рассмотрим один из таких фрактальных объектов - триадную кривую Коха. Построение кривой начинается с отрезка единичной длины (рис. 1.6) - это 0-е поколение кривой Кох. Далее каждое звено (в нулевом поколении один отрезок) заменяется на образующий элемент, обозначенный на рис.1 через n=1. В результате такой замены получается следующее поколение кривой Кох. В 1-ом поколении - это кривая из четырех прямолинейных звеньев, каждое длиной по 1/3. Для получения 3-го поколения проделываются те же действия - каждое звено заменяется на уменьшенный образующий элемент. Итак, для получения каждого последующего поколения, все звенья предыдущего поколения необходимо заменить уменьшенным образующим элементом. Кривая n -го поколения при любом конечном n называется предфракталом. На рис. 1.6 представлены пять поколений кривой. При n стремящемся к бесконечности кривая Кох становится фрактальным объектом.

 

20. Геометрические фракталы: салфетка Серпинского.

Рассмотрим самоподобную фигуру, придуманную польским математиком В.Серпинским (1882–1969).

Она получается из квадрата последовательным вырезанием серединных квадратов. Проследим построения нового квартала более подробно. Разделим данный квадрат на девять равных квадратов и квадрат, расположенный в середине, вырежем. Получим квадрат с пустотой (рис. 10а). Для оставшихся восьми квадратов вновь повторим указанную процедуру. Разделим каждый из них на девять равных квадратов и серединные квадраты удалим (рис. 10б). Повторяя похожие построения, будем получать все более “дырявую” фигуру (рис. 10в). То, что остается после всех вырезаний, и будет ковром Серпинского.

а) б) в)

Рис. 10

Поскольку вырезаемые квадраты располагаются все более часто, то в результате на ковре (салфетке) Серпинского не будет ни одного, даже самого маленького, квадрата без «дырки».

Начиная не с квадрата, а с равностороннего треугольника, и вырезая центральные треугольники, получим еще одну самоподобную фигуру, аналогичную ковру Серпинского. Она носит название «салфетки Серпинского» (рис. 11).

Рис. 11

 

 

21. Фрактал Кантора.

Георг Кантор (1845-1918) явился одним из основателей теории множеств. Он также придумал один из старейших фракталов - множество Кантора (описано им в 1883) (называют иногда пылью). Фрактальные свойства пыли Кантора имеют огромное значение, особенно учитывая тот факт, что многие известные фракталы являются близкими родственниками этого фрактала.

Кантор с помощью простой рекурсивной (повторяющейся) процедуры превратил линию в набор несвязанных точек (так называемая Пыль Кантора). Он брал линию и удалял центральную треть и после этого повторял то же самое с оставшимися отрезками.

Способ построения этого множества следующий. Берётся отрезок прямой единичной длины. Затем он делится на три равные части, и вынимается средний отрезок. Это первый шаг итерационной процедуры. На втором шаге подобной процедуре деления на три равные части и последующего удаления середины подвергается каждый из двух оставшихся отрезков. Так продолжая до бесконечности, получим множество Кантора. Нетрудно заметить, что суммарная длина получившихся в пределе отрезков равна нулю, так кам мы исключили в результате длину, равную 1:

Проведём построение более формально на множестве. Берём отрезок единичной длины . Удаляем из него открытый интервал , получая . На следующем и всех остальных шагах вы выкидываем среднюю треть (не включая концы) всех отрезков текущего уровня. Т. о. на втором шаге мы имеем . Предельное множество , которое представляет собой пересечение множеств , , и представляет собой пыль Кантора.

Множество Кантора имеет мощность континуума. Для этого необходимо установить взаимно однозначное соответствие между точками из множества Кантора и точками отрезка . Будем представлять все точки отрезка в виде двоичной дроби, а точки пыли Кантора в виде троичной дроби. В случае, когда точка имеет два представления, мы будем всегда выбирать то, которое заканчивается всеми единицами в двоичном виде и всеми двойками в троичном. Заметим, что точка попадает в множество Кантора тогда и только тогда, когда в ее троичном представлении присутствуют только нули и двойки, поэтому искомое соответствие осуществляется заменой всех двоек в троичном представлении на единицы. Описанная процедура и определяет ваимно однозначное соответствие между множеством Кантора и отрезком .

Непосредственно с множеством Кантора связана чёртова лестница.

 

 

22. Фрактальная размерность. Примеры вычисления размерности фракталов.

Фрактал – множество с дробной размерностью.

Фрактал – множество, размерность Хайсдорфа-Безиковича которого строго больше топологической размерности.

Типы размерности:

1) Евклидова: минимальное число координат, необходимых для однозначного определения положения точки;

2) Тополог.: размерность любого множества на 1 больше размерности разреза, делящего его на две несвязнае части (тополог.размерность отрезка-1, топол.разм. квадрата-2, плоскости-2);

3) Размерность самоподобия . Размерность самоподобия – один из частных случаев фрактальной размерности.

Размерность Хаусдорфа — естественный способ определить размерность подмножества в метрическом пространстве.

Размерность Хаусдорфа согласуется с нашими обычными представлениями о размерности в тех случаях, когда эти обычные представления есть. Например, в трёхмерном евклидовом пространстве хаусдорфова размерность конечного множества равна нулю, размерность гладкой кривой — единице, размерность гладкой поверхности — двум и размерность множества ненулевого объёма — трём. Для более сложных (фрактальных) множеств размерность Хаусдорфа может не быть целым числом.

 

23. Алгебраические фракталы: метод построения алгебраических фракталов.

Свое название эти фракталы получили за то, что их строят на основе алгебраических формул.

Примеры: множество Мандельброта, множество Жюлиа, фрактал Ньютона.

Метод:

1. Выбирается формула (функция), в нее подставляется число и получается результат.

2. Полученный результат подставляется в эту же формулу и получается следующее число.

3. Повторение процедуры.

4. Получается набор чисел, являющихся точками фрактала.

Функция для разных точек может иметь разное поведение:

1. Стремится к бесконечности.

2. Стремится к 0.

3. Принимает несколько фиксированных значений.

4. Хаотичное поведение.

 

24 вопрос. Множество Мандельброта (один из самых известных фрактальных объектов) впервые было построено (визуально с применением ЭВМ) Бенуа Мандельбротом весной 1980 г. в исследовательском центре фирмы IBM им. Томаса Дж. Уотсона. И хотя исследования подобных объектов начались ещё в прошлом веке, именно открытие этого множества и совершенствование аппаратных средств машинной графики в решающей степени повлияли на развитие фрактальной геометрии и теории хаоса. Итак, что же такое множество Мандельброта.

Рассмотрим функцию комплексного переменного . Положим и рассмотрим последовательность , где для любого . Такая последовательность может быть ограниченной (т.е. может существовать такое r, что для любого 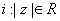) либо "убегать в бесконечность" (т.е. для любого r > 0существует 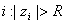). Множество Мандельброта можно определить как множество комплексных чисел c, для которых указанная последовательность является ограниченной. К сожалению, не известно аналитического выражения, которое позволяло бы по данному c определить, принадлежит ли оно множеству Мандельброта или нет. Поэтому для построения множества используют компьютерный эксперимент: просматривают с некоторым шагом множество точек на комплексной плоскости, для каждой точки проводят определённое число итераций (находят определённое число членов последовательности) и смотрят за её "поведением". (Рис. 4).

Доказано, что множество Мандельброта размещается в круге радиуса r=2 с центром в начале координат. Таким образом, если на некотором шаге модуль очередного члена последовательности превышает 2, можно сразу сделать вывод, что точка, соответствующая c, определяющему данную последовательность, не принадлежит множеству Мандельброта.

Уменьшая шаг, с которым просматриваются комплексные числа, и увеличивая количество итераций, мы можем получать сколь угодно подробные, но всегда лишь приближённые изображения множества.

Пусть в нашем распоряжении имеется N цветов, занумерованных для определённости от 0 до N-1. Будем считать, опять же для определённости, что черный цвет имеет номер 0. Если для данного c после N-1 итераций точка не вышла за круг радиуса 2, будем считать, что c принадлежит множеству Мандельброта, и покрасим эту точку c в чёрный цвет. Иначе, если на некотором шаге k (k Є [1; N-1]) очередная точка вышла за круг радиуса 2 (т.е. на k-ом шаге мы поняли, что она "убегает"), покрасим её в цвет k.

Красивые изображения получаются при удачном выборе палитры и окрестности множества (а именно вне множества мы и получим "цветные точки). (Рис. 5, 6).

Рис. 4

Рис. 5 Рис. 6

25. Основные понятия теории узлов

Модель узла - замкнутая, несамопересекающаяся кривая в пространстве.

Узел – это замкнутая линия в пространстве, гладкая или ломаная, которая может быть как угодно закручена и переплетена.

Под развязыванием узла будем понимать выпрямление этого отрезка путем деформации его в трехмерном пространстве.

тривиальный узел (окружность)

 

Изображение узла называется диаграммой узла.

Зацеплением называется конечный набор замкнутых непересекающихся ориентированных ломаных в пространстве.

Два узла называются изотопными (эквивалентными), если от одного к другому можно перейти последовательно выполняя преобразования, которые называются элементарными изотопиями.

Два узла изотопны, если один узел можно перевязать в другой, не разрезая его и не допуская самопересечений.