Кафедра математики и информатики
Профессор Васильев В.П.
Контрольная работа ПО ДИСЦИПЛИНЕ
«Исследование операций»
Ми-ЗКМ-401 (3 к 5 сем)
Выбор варианта по 4 цифре в зачетке
Общие требования
Индивидуальное задание состоит в решении 4 задач. Две задачи выполняются с использованием программной системы MSEXCEL, а две « в ручную» использованием теоретических наработок.
Варианты заданий выбираются по четвертой цифре зачетной книжки или первой цифре в порядковом номере списка группы (например: 218003 –10 вариант, 218203 – 2 вариант) или студент имеет номер 12 в списке –вариант 2
1. Отчет по заданию должен быть выполнен в редакторе документов Word, параметры страницы- книжная, поля все 20 мм.
2. Структура задания: первый лист – титульный, каждый освещаемый вопрос оформляется с новой страницы.
3. Шрифт Times New Roman - 12пт, междустрочный интервал – одинарный, выравнивание по левому краю.
4. Общий объем работы – не более6 страниц печатного текста, включая рисунки, таблицы, графики, схемы
Варианты заданий
Задание 1. Составить и решить графическим методом следующую задачу линейного программирования:
Из трех сортов бензина образуется две смеси. Первая состоит из 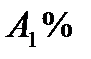 бензина первого сорта,
бензина первого сорта, 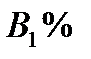 бензина второго сорта,
бензина второго сорта, 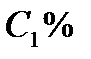 бензина третьего сорта; вторая
бензина третьего сорта; вторая 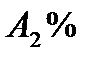 -1-го,
-1-го, 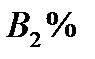 - 2-го,
- 2-го, 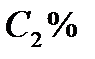 -3-го сорта. Цена первой смеси – 305 у.е., второй – 200 у.е. за тонну. Сколько смеси первого и второго вида можно изготовить из «а» тонн первого сорта, «b» тонн второго сорта и «с» тонн третьего сорта, чтобы получить максимальный доход?
-3-го сорта. Цена первой смеси – 305 у.е., второй – 200 у.е. за тонну. Сколько смеси первого и второго вида можно изготовить из «а» тонн первого сорта, «b» тонн второго сорта и «с» тонн третьего сорта, чтобы получить максимальный доход?
| № задач |  |  | 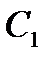 | 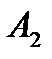 | 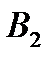 | 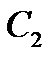 | 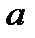 | b | с |
Задание 2. Предприятие производит 3 вида обуви: 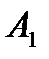 ,
, 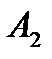 ,
, 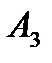 используя при этом кожу двух видов
используя при этом кожу двух видов 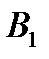 ,
, 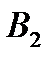 ,
, 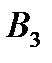 . Известны затраты кожи i-го вида на единицу готового изделия j-го вида
. Известны затраты кожи i-го вида на единицу готового изделия j-го вида 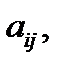 запасы кожи вида
запасы кожи вида 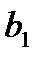 (i=1,2), а также прибыль, полученная от единицы готового изделия j-го вида
(i=1,2), а также прибыль, полученная от единицы готового изделия j-го вида 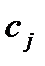 (j = 1, 2, 3).
(j = 1, 2, 3).
Сколько обуви каждого вида необходимо произвести, чтобы получить максимум прибыли? Задачу решить Симплекс методом и проверить с помощью надстройки Поиск Решения MSExcel
Обозначения: в таблице приведена матрица затрат А = 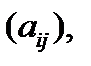 справа от таблицы значение
справа от таблицы значение 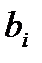 = (j = 1,2) и внизу -
= (j = 1,2) и внизу - 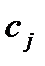 = (j=1,2,3).
= (j=1,2,3).
1. 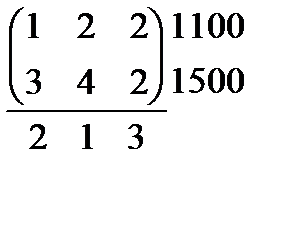 2.
2. 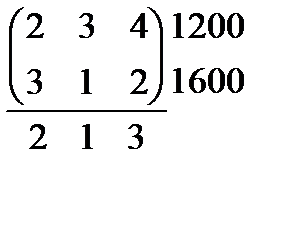 3.
3. 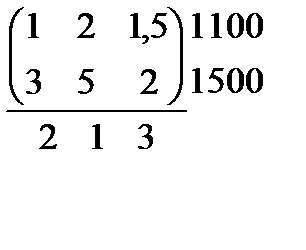 4.
4. 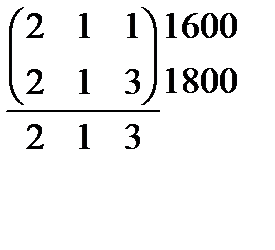
5. 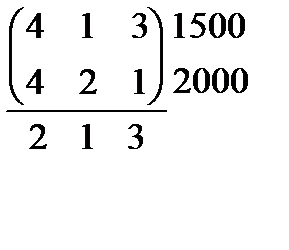 6.
6. 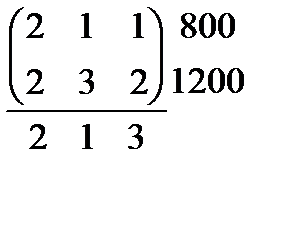 7.
7. 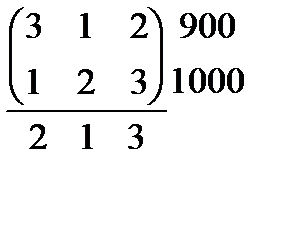 8.
8. 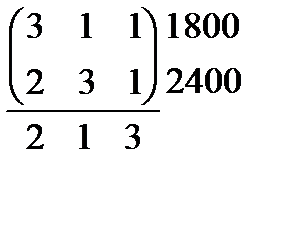
9. 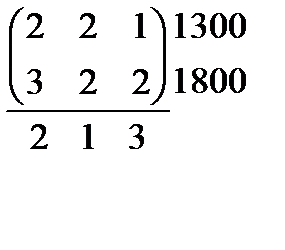 10.
10. 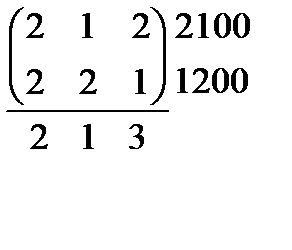
Задание 3 На предприятии имеется возможность выпуска и видов продукции Пj (j = 1,2,3,4). При ее изготовлении используются ресурсы Р1, Р2, Р3. Размеры допустимых затрат ресурсов ограничены соответственно величинами В1, В2, В3. Расход ресурса i-го вида (i = 1,2,3) на единицу продукции j-го вида составляет аij единиц. Цена единицы продукции j-го вида равна С1.
Требуется: построить математическую модель процесса и найти план выпуска продукции, обеспечивающий предприятию максимальный доход. Записать и решить двойственную задачу.Решения выполнить с помощью надстройки Поиск Решения MSExcel
Вариант 1 А: 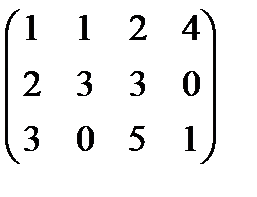 В: В: 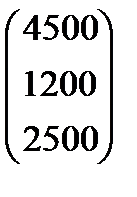 С: С:  | Вариант 2 А: 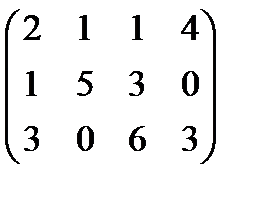 В: В: 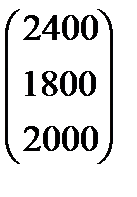 С: С: 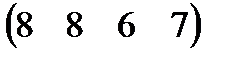 |
Вариант 3 А: 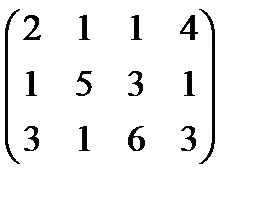 В: В: 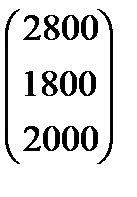 С: С: 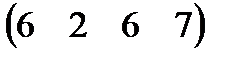 | Вариант 4 А: 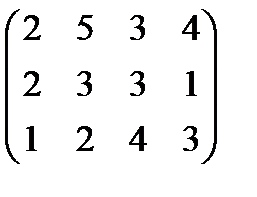 В: В:  С: С: 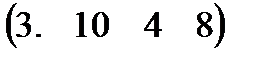 |
Вариант 5 А: 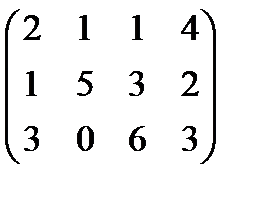 В: В:  С: С: 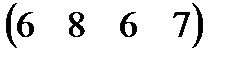 | Вариант 6 А= 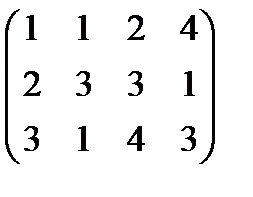 В: В: 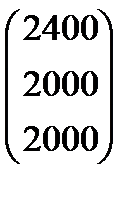 С: С: 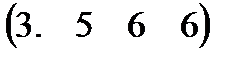 |
Вариант 7 А: 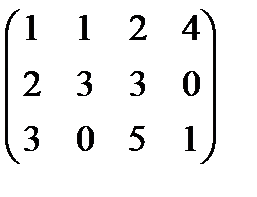 В: В: 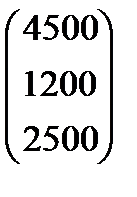 С: С: 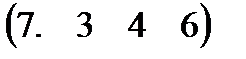 | Вариант 8 А: 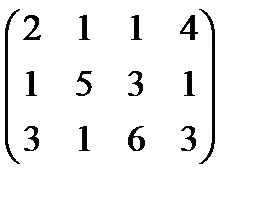 В: В:  С: С: 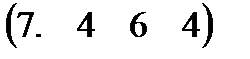 |
Вариант 9 А: 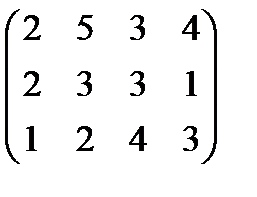 В: В:  С: С: 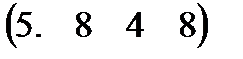 | Вариант 10 А: 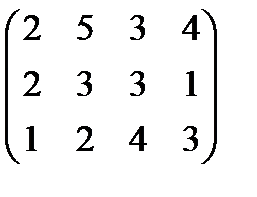 В: В:  С: С: 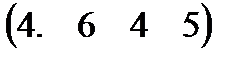 |
Задание 4. Три хлебозавода  (i= 1,2,3) выпускают ежедневно хлеб в количестве
(i= 1,2,3) выпускают ежедневно хлеб в количестве 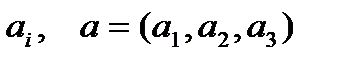 килограмм соответственно. Необходимо доставить их в четыре магазина
килограмм соответственно. Необходимо доставить их в четыре магазина 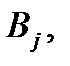 (j =1,2,3,4) в количестве
(j =1,2,3,4) в количестве 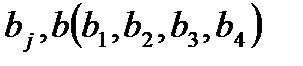 килограмм соответственно. Стоимость перевозки от i-го хлебозавода к j-му магазину определяется матрицей транспортных издержек
килограмм соответственно. Стоимость перевозки от i-го хлебозавода к j-му магазину определяется матрицей транспортных издержек
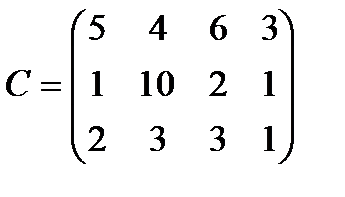
Составить план перевозок, позволяющий удовлетворить все потребности и имеющий минимальную стоимость. Найти начальный опорный план и решить с помощью настройки поиск решения MSExcel, данные определяются из таблицы:
| а = (100,150,50) | b = (75,75,150,50) | |
| а.= (200,300,100) | b = (150,150,300,100) | |
| а= (300,450,150) | b = (300,250,300,150) | |
| а= (400,600,200) | b = (300,300,500,400) | |
| а= (500,700,200) | b = (375,375,625,125) | |
| а= (600,900,300) | b = (500,500,750,200) | |
| а= (700,1050,350) | b = (800,800,1000,200) | |
| а= (800,1200,400) | b = (600,600,1000,200) | |
| а= (900,1400,450) | b = (700,800,1200,200) | |
| а= (1000,1500,500) | b = (750,750,1500,250) |
Пример выполнения индивидуального задания
Задача 1.
Фабрика изготовляет два вида красок: для внутренних работ (В) и наружных работ (Н). Для производства красок используется два вида сырья И1, И2. Максимально возможные суточные запасы сырья составляют соответственно 6 т. и 8 т. Нормативные расходы сырья при производстве красок приведены в табл.
Нормативы расхода сырья на 1 т краски
| Сырье | Краска | |
| Н | В | |
| И1 | ||
| И2 |
Изучение рынка сбыта показало, что суточный спрос на краску В никогда не превышает спроса на краску Н более, чем на 1т. Оптовые цены одной тонны краски Н – 3 тыс.у.е., краски В – 2 тыс.у.е.. Какое количество краски каждого вида должна производить фабрика, чтобы выручка от реализации была максимальной.
Решение.
Этап 1. Построение экономико-математической модели данной задачи.
Полагая, что x1 и x2 – соответственно суточные объемы производства красок Н и В, условия ограничения на суточный расход сырья И1 и И2 в формальном виде соответственно запишутся:
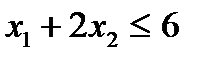 , (1.1)
, (1.1)
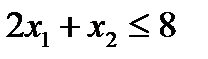 . (1.2)
. (1.2)
Условия, что суточное предложение красок должно удовлетворять спросу, в формальном виде имеют вид:
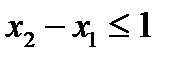 , (1.3)
, (1.3)
Объемы производства не могут быть отрицательными
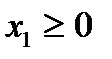 ,
, 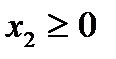 . (1.4)
. (1.4)
Условие достижения максимума выручки от реализации записывается в виде целевой функции:
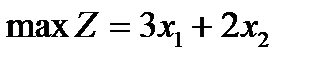 . (1.5)
. (1.5)
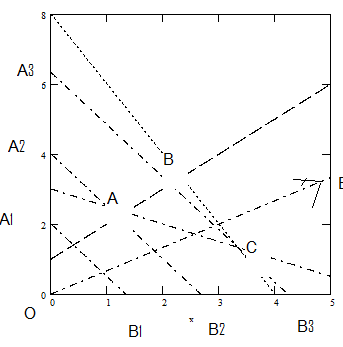
Этап 2. Построение области допустимых решений.
Рассмотрим координатную плоскость (0,х1,х2) неравенства (4) показывают, что область допустимых решений первый квадрант координатной плоскости.
Каждое из неравенств (1)-(3) определяет полуплоскость, ограниченную прямой
ах1+вх2=с
Построим их изображения на чертеже.
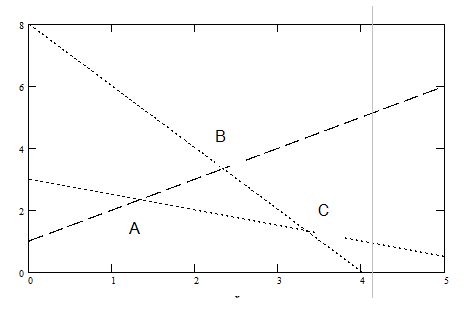
Координаты точек (х1, х2) находящихся внутри треугольника АВС, удовлетворяют одновременно всем неравенствам 1-3
Рассмотрим выражение (5). 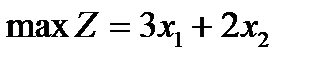 .
.
Придадим переменной zзначения 2, 4,6 ….на координатной плоскости мы будем получать семейства параллельных прямых (А1В1), (А2,В2), (А3,В3), называются линиями уровня функции z.Линии уровня перпендикулярны вектору ОС (3,2), который называется вектором градиента функции z.Его координаты-частные производные zпо переменным х1 и х2Последняя С, которая является точкой выхода линий уровня за пределы треугольника. Значение Zявляется максимальным значением этой функции. Координаты С легко вычислить они составляют 10/3 и 4/3, а значение Z=12/3
Задача 2. Предприятие выпускает четыре вида продукции П1, П2, П3 и П4. Для производства продукции оно располагает тремя ресурсами, запасы которых ограничены величинами 35, 30 и 40 единиц. Удельные затраты на единицу продукции и цена единицы готовой продукции заданы в виде таблицы:
| Ресурсы | Расход ресурсов на единицу продукции | |||
| П1 | П2 | П3 | П4 | |
| Р1 Р2 Р3 | ||||
| Цена (ден.ед.) |
Требуется определить производственную программу предприятия, обеспечивающую максимальный доход.
Решение:
Составим математическую модель задачи. Пусть х1, х2, х3 и х4 ― искомые объемы производства продукции, а через f ― доход предприятия от производства и реализации всей продукции, который с учетом введенных обозначений определяется следующей функцией:
f = 14х1+ 10х2+ 14х3+ 11х4  max. (2.1)
max. (2.1)
Ограничения по используемым ресурсам примут вид:
4х1+ 2х2+ 2х3+ 3х4  35,
35,
х1+ х2 + 2х3+ 3х4  30, (2.2)
30, (2.2)
3х1+ х2+ 2х3+ х4  40.
40.
По смыслу задачи объемы производства продукции не могут быть отрицательными, поэтому
хj  0, j=.1,2,3,4
0, j=.1,2,3,4
Введем в рассмотрение возможные остатки ресурсов: х5, х6, х7, или приведем модель задачи к каноническому виду и получим:
f = 14х1+ 10х2+ 14х3+ 11х4  max
max
4х1+ 2х2+ 2х3+ 3х4 + х5 = 35, (2.3)
х1+ х2 + 2х3+ 3х4 + х6 =30,
3х1+ х2+ 2х3+ х4 + х7 = 40.
хj  0, (j=1-7)
0, (j=1-7)
Выделим начальный базис системы, т.е. выделить базисные переменные. Базисных переменных должно быть столько, сколько ограничений системы линейных уравнений, т.е. в нашем случае их должно быть три. Наши дополнительные переменные х5, х6, х7 и будут базисными, так как им соответствуют единичные векторы, которые образуют базис в трехмерном пространстве. Выразим эти переменные и получим:
х5 = 35 - (4х1+ 2х2+ 2х3+ 3х4),
х6 = 30 - (х1+ х2 + 2х3+ 3х4), (2.4)
х7 = 40 – (3х1+ х2+ 2х3+ х4).
Итак у нас х5, х6, х7 базисные переменные, а х1, х2, х3 и х4 будут свободными переменными. Полагая свободные переменные нулю получим х5 =35, х6 =30, х7 =40. План 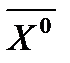 = (0; 0; 0; 0; 35; 30; 40) удовлетворяет одновременно всем ограничениям задачи и следовательно является опорным планом. Занесем условия задачи в симплексную таблицу (таблица 1). Первый столбец ─ столбец базисных переменных (БП ─ х5, х6, х7); второй столбец ─ столбец свободных коэффициентов (1); далее идут столбцы свободных переменных (СП) ─ таких переменных в нашей задаче четыре (х1, х2, х3 и х4), они всегда записываются в (СП) со знаком "-". Чтобы правильно вписать коэффициенты в таблицу данного вида, надо придерживаться следующего правила: в соответствующей строке записываем числа так, чтобы при умножении их на соответствующее значение в "заголовках" таблицы мы получили бы выражения вида (1. 2.4)
= (0; 0; 0; 0; 35; 30; 40) удовлетворяет одновременно всем ограничениям задачи и следовательно является опорным планом. Занесем условия задачи в симплексную таблицу (таблица 1). Первый столбец ─ столбец базисных переменных (БП ─ х5, х6, х7); второй столбец ─ столбец свободных коэффициентов (1); далее идут столбцы свободных переменных (СП) ─ таких переменных в нашей задаче четыре (х1, х2, х3 и х4), они всегда записываются в (СП) со знаком "-". Чтобы правильно вписать коэффициенты в таблицу данного вида, надо придерживаться следующего правила: в соответствующей строке записываем числа так, чтобы при умножении их на соответствующее значение в "заголовках" таблицы мы получили бы выражения вида (1. 2.4)
Таблица 1
| БП | СП | ||||
| - х1 | - х2 | - х3 | - х4 | ||
| х5 = | |||||
| х6 = | |||||
| х7 = | |||||
| f = | -14 | -10 | -14 | -11 |
При решении задачи максимизации в строке целевой функции в столбцах свободных переменных не должно быть отрицательных коэффициентов. Из таблицы, видно, что в столбцах свободных переменных в индексной строке (f) присутствуют отрицательные коэффициенты, поэтому данный опорный план не является оптимальным. Улучшим его, переходя от одного базиса системы к другому. Выберем разрешающий столбец, как столбец, соответствующий наибольшей по модулю отрицательной оценке, т.е.
max  {│-14│; │-10│; │-14│; │-11│} = 14.
{│-14│; │-10│; │-14│; │-11│} = 14.
Из двух одинаковых оценок выберем одну, например, столбец соответствующий свободной переменной х1, он и будет разрешающим столбцом. Затем находим разрешающую строку по наименьшему симплексному отношению:
min { 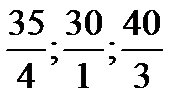 } =
} = 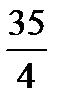 .
.
На пересечении разрешающего столбца и разрешающей строки находим разрешающий элемент, выделяем его (мы выделили ячейку, в которой находится разрешающий элемент, равный 4). Строим следующую симплексную таблицу, меняя две переменные х1 и х5 местами и пересчитываем элементы по правилам симплексных преобразований. (См приложение 1)
Таблица 2
| БП | СП | min | ||||
| - х5 | - х2 | - х3 | - х4 | |||
| х1 | 35/4 | 1/4 | 2/4 | 2/4 | ¾ | 35*4/4*2=35/2 |
| х6 | 85/4 | -1/4 | 2/4 | 6/4 | 9/4 | 85*4/4*6=85/6 |
| х7 | 55/4 | -3/4 | -2/4 | 2/4 | -5/4 | 55*4/4*2=55/2 |
| f | 490/4 | 14/4 | -12/4 | -28/4 | -2/4 |
Из таблицы 2 видно, что в строке f присутствуют отрицательные элементы данный план не является оптимальным. Повторим наши преобразования, выбрав разрешающий элемент, равный 6/4. В результате получим следующую таблицу.
Таблица 5
| БП | СП | min | ||||
| - х5 | - х2 | - х6 | - х4 | |||
| х1 | 10/6 | 2/6 | 2/6 | -2/6 | (10/6)/(2/6)=10/2 | |
| х3 | 85/6 | -1/6 | 2/6 | 4/6 | 9/6 | (85/6)/(2/6)=85/2 |
| х7 | 40/6 | -4/6 | -4/6 | -2/6 | -12/6 | ─ |
| f | 1330/6 | 14/6 | -4/6 | 28/6 | 60/6 |
Еще раз проводя преобразования с элементами данной таблицы, получим оптимальный план, который находится в таблице 3.
В индексной строке последней таблицы нет ни одного отрицательного элемента, следовательно, содержащийся в ней план является оптимальным. Выпишем его, зная, что значения базисных переменных находится в столбце свободных коэффициентов, а все свободные переменные равны нулю: х2=5; х3=12,5; х7=10; х5=0; х1=0; х6=0; х4=0 или план 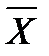 =(0;5;12,5;0;0;0;10). Значение целевой функции равно 225.
=(0;5;12,5;0;0;0;10). Значение целевой функции равно 225.
Таблица 3
| БП | СП | ||||
| - х5 | - х1 | - х6 | - х4 | ||
| х2 | -1 | ||||
| х3 | 12,5 | -0,5 | -1 | 1,5 | |
| х7 | -1 | -2 | |||
| f |
Таким образом предприятию по оптимальному плану следует производить 5 единиц продукции вида П2, 12,5 единиц продукции вида П3, продукции П1 и П4 выпускать не следует, при этом ресурсы Р1 и Р2 будут израсходованы полностью, а ресурс Р3 останется в количестве 10 единиц. Выручка предприятия при этом составит 225 ден.ед.
Выполнить проверку MSExcel используя методику задачи 3
Задача 3 На предприятии имеется возможность выпуска и видов продукции Пj (j = 1,2,3). При ее изготовлении используются ресурсы Р1, Р2, Р3. Размеры допустимых затрат ресурсов ограничены соответственно величинами В1, В2, В3. Расход ресурса i-го вида (i = 1,2,3) на единицу продукции j-го вида составляет аij единиц. Цена единицы продукции j-го вида равна С1. С1 Требуется: построить математическую модель процесса и найти план выпуска продукции, обеспечивающий предприятию максимальный доход. Записать двойственную задачу
| В1 | В2 | В3 | a11 | a12 | a13 | a21 | a22 | a23 | a31 | a32 | a33 | С1 | С2 | С3 |
Обозначим План выпуска П1-х1, П2-х2 П3-х3
Модель процесса
10х1+10х2+12х3≤300 x1≥0, x2≥0, x3≥0
5x1+4x2+3x3≤190
3x1+5x2+3x3≤180
Функция дохода maxZ= 15х1+20x2+10x3
Расчет выполним процедурой «Поиск решения.
На рабочем листе создадим схему решения.
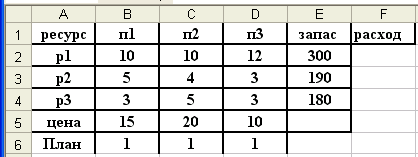
Присвоим ячейкам столбца Е имя запас, столбца F имя расход, строки 5 имя цена, строки 6 имя план. Процедура вMSExcel 2010 Выделить блок ячеек(строку, столбец) /контекстное меню/
Присвоить имя.
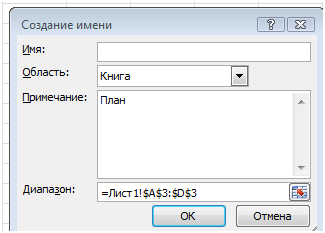
В столбец расход занесем формулу СУММА ПРОИЗ (В2:D2; План)
И скопируем ее на все строки 1-5
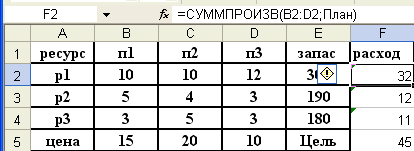
Выполним поиск решения.
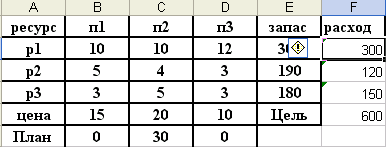
Условия поиска
Цель ячейка F5
Изменяемые ячейки: План
Ограничения: План больше нуля
Расход меньше запаса.
Результат поиска
 2017-12-14
2017-12-14 1858
1858