Тема: Электрические станции и подстанции
Лекция№10. ЭЛЕКТРОДИНАМИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ ПРОВОДНИКОВ С ТОКАМИ В СХЕМАХ ЭНЕРГОУСТАНОВОК.
Оглавление
10.1 Силы взаимодействия двух проводников. 1
10.2 Силы в трехфазной системе проводников. 3
10.3 Электродинамическая стойкость жёстких проводников. 4
10.4 Выбор изоляторов. 5
10.5 Электродинамическая стойкость гибких проводников. 6
10.6 Электродинамическая стойкость аппаратов. 7
При КЗ проводники и аппараты подвергаются воздействию значительных электродинамических сил, которые могут достигать 4000 – 16000 Н. Эти силы могут вызвать остаточную деформацию жёстких проводников, схлестывание гибких проводников, вызвать отказ во включении выключателей или самопроизвольное отключение разъединителей. Чтобы этого не случилось, все системы токоведущих частей и электрические аппараты проверяются на электродинамическую стойкость при проектировании первичной электрической схемы.
Из физики известно, что на элемент проводника dl с током i в магнитном поле с индукцией B действует сила dF=iBdlsinα. Магнитное поле может быть создано другим проводником с током, тогда говорят о взаимодействии двух проводников с токами.
Магнитную индукцию от проводника с током можно определить с помощью закона Био-Савара, но иногда бывает удобнее определить В с помощью закона полного тока:  .
.
Силы взаимодействия двух проводников.
Часто взаимодействие между проводниками в схемах энергоустановок сводится к взаимодействию двух параллельных проводников с токами. Рассмотрим этот случай подробнее (Рис.10.1). Пусть проводники длиной l находятся на расстоянии а. Ток в одном проводнике i1, в другом i2. Будем считать, что l»а (это часто имеет место на практике), тогда для вычисления индукции В1 от первого проводника в районе второго воспользуемся законом полного тока.

Рис. 10.1 Взаимодействие двух проводников с токами и определение направления силы с помощью правила левой руки
В качестве контура интегрирования L выберем окружность с радиусом а. Тогда получим  , т.к. в силу симметрии В1=const на контуре L, то можно записать
, т.к. в силу симметрии В1=const на контуре L, то можно записать  . Из последнего выражения можно записать для индукции от первого проводника в районе второго:
. Из последнего выражения можно записать для индукции от первого проводника в районе второго:  . Зная индукцию В1, можно определить силу dF2 действующую на элемент dl2 второго проводника с током i2.
. Зная индукцию В1, можно определить силу dF2 действующую на элемент dl2 второго проводника с током i2.
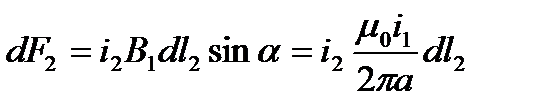 .
.
В нашем случае sinα=1, т.к. α=π/2, поэтому сила, действующая на весь второй проводник:
 .
.
В практических расчетах динамической стойкости пользуются понятием погонной силы fпог=F/l [Н/м]. Для нашего случая с учётом того, что μ0=4π10-7Гн/м, выражение для погонной силы примет вид:
 .
.
Т.е. погонная сила пропорциональна произведению токов во взаимодействующих проводниках и обратнопропорциональна расстоянию между ними.
В предыдущих формулах предполагалось, что взаимодействующие проводники бесконечно тонкие. Для проводников конечного сечения:
 , где кф – коэффициент формы проводника, значения которого приводится в справочниках.
, где кф – коэффициент формы проводника, значения которого приводится в справочниках.
 2017-12-14
2017-12-14 874
874







