Лекція №6 Молекулярно-кінетична теорія
Статистичний підхід до опису великих систем
Зв’язок між мікро- та макропараметрами системи
Головні постулати МКТ. Поняття ідеального газу
Основне рівняння МКТ та рівняння Менделєєва-Клапейрона
Реальні гази. Рівняння Ван-дер-Ваальса
ü СТАТИСТИЧНИЙ ПІДХІД ДО ОПИСУ ВЕЛИКИХ СИСТЕМ
Сучасна статистична фізика виходить з гіпотези, яка відома вже понад дві тисячі років, ще з епохи античного світу. Вважається, що всі фізичні (макроскопічні) тіла складаються з безлічі мікрочастинок. Ці мікрочастинки перебувають у безперервному, тобто безупинному, та випадковому (хаотичному, невпорядкованому) русі. Така точка зору висловлювалася ще давньогрецькими філософами Демокрітом та Епікуром, а пізніше викладена римським поетом Титом Лукрецієм Каром (95-55 р. до Р.Х.) у філософській поемі “Про натуру речей”.
Структурні елементи, з котрих побудована макросистема (макротіло), називатимемо мікрочастинками.
Далі ця так звана атомістична гіпотеза розвивалася в роботах хіміків-атомістів, зокрема Ломоносова та Лавуаз’є, у XVIII-XIX сторіччях. Фізичні основи молекулярно-кінетичної теорії (МКТ), як попередниці статистичної фізики, були закладені більше ста років тому дослідженнями Максвела (1866), Больцмана (1872) та, трохи пізніше, Гіббса. Максвел, вивчаючи розподіл молекул ідеального газу по швидкостям, першим застосував ймовірносно-статистичний підхід для вивчення великих сукупностей частинок (з числом частинок порядку числа Авогадро – 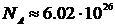 ).
).
Гіббс (1839-1903) завершив розробку основи статистичної фізики (її ще звуть статистичною механікою), запропонувавши альтернативний підхід з використанням нового поняття ансамблів частинок.
Статистична фізика обмежується розглядом властивостей макроскопічних великих систем частинок (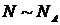 ), стан яких не змінюється в часі, тобто є стаціонарним. Такі стаціонарні стани, в яких система може перебувати необмежено довго, причому якщо на додаток всі параметри системи є ще й однорідними (незалежними від координат), називають рівноважними станами.
), стан яких не змінюється в часі, тобто є стаціонарним. Такі стаціонарні стани, в яких система може перебувати необмежено довго, причому якщо на додаток всі параметри системи є ще й однорідними (незалежними від координат), називають рівноважними станами.
Можна сказати, що статистична фізика вивчає поведінку та властивості рівноважних макросистем. На відміну від статистичної фізики, фізична кінетика, наприклад, вивчає поведінку нерівноважних систем. Тобто таких систем, які є, або нестаціонарними, змінними в часі, або неоднорідними в просторі, або і те і інше разом. Зрозуміло, що такі об’єкти дослідження є більш складними, тому закони фізичної кінетики значно складніші від законів статистичної фізики.
Системи частинок (дискретні та суцільні) розглядалися нами також в механіці. В принципі опис руху кожної частинки системи можна зробити на основі законів механіки, вживаючи, наприклад, методи класичної теоретичної механіки, або навіть і квантової механіки. Все ж, такий динамічний підхід до опису руху системи через повний опис руху кожної її частинки має певні природні обмеження. Припустимо, навіть, що ми здатні обчислити траєкторію кожної мікрочастинки всього за один такт роботи сучасного мікропроцесора (для частот порядку 1 ГГц цей час складає приблизно 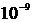 секунди). Але й тоді за повний рік безперервної роботи комп’ютера ми зможемо обрахувати траєкторії в системі, яка складається не більше, ніж з
секунди). Але й тоді за повний рік безперервної роботи комп’ютера ми зможемо обрахувати траєкторії в системі, яка складається не більше, ніж з 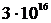 частинок. До числа Авогадро
частинок. До числа Авогадро 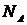 , не вистачає ще добрих десяти порядків. Таким чином, час обліку для реальної великої системи складе понад
, не вистачає ще добрих десяти порядків. Таким чином, час обліку для реальної великої системи складе понад 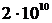 років.
років.
Втім, навіть результати річного обліку порівняно невеличкої системи частинок є відверто надмірними інформаційно, оскільки ми ніколи не зможемо не те, що осягнути, чи проаналізувати отриманий результат, але навіть видрукувати його на папері і проглянути. Отже, динамічний метод дослідження систем частинок є адекватним і придатним лише для порівняно невеликих, стосовно кількості структурних елементів, систем.
Отже, потрібен метод оцінки, можливо, навіть наближеної оцінки, невеликої кількості макропараметрів, характеризуючи систему в цілому. При знаходженні цих макроскопічних характеристик системи, ми беремо під увагу лише мінімальну кількість мікропараметрів для тих структурних елементів, з яких побудована система.
Окрім того, слід визначити, які саме мікропараметри цих структурних елементів системи треба утримати, а які відкинути при таких оцінках для того, аби знайдені оцінки макропараметрів були максимально надійними.
Такий метод дослідження систем принципово відрізняється від динамічного і має назву статистичного методу. Він, в принципі, повинен бути тим точніший, чим більшою є досліджувана система. Як бачимо, статистичний та динамічний методи у фізиці не стільки є конкуруючими, скільки взаємно доповнюють один до одного.
Великі макросистеми мають важливу принципову особливість: їх поведінка в рівноважному стані регулюється законами, зміст яких порівняно слабо залежить від конкретних властивостей, і навіть від особливостей взаємодії, тих мікрочастинок, що з них побудована макросистема. Ця принципова особливість є відображенням відомого в математиці закону великих чисел, або статистичного закону.
ü ЗВ’ЯЗОК МІЖ МІКРО- ТА МАКРОПАРАМЕТРАМИ СИСТЕМИ
Закон великих чисел дозволяє розвинути такий підхід до вивчення макросистем, який взагалі ігнорує внутрішню структуру великої макросистеми, тобто розглядає її як деяке “неструктуроване суцільне середовище”. Історично такий підхід сформувався навіть раніше статистичної фізики (СФ) і отримав свого часу назву термодинаміка (ТД). Надзвичайна загальність ТД дозволила побудувати її на основі декількох, фактично трьох, аксіом (законів, постулатів), що дозволяє описувати систему лише через невелику кількість її макропараметрів. Тобто такі параметри, які стосуються всієї системи, як цілого. Зрозуміло, що ніякі мікропараметри (тобто характеристики мікрочастинок) не фігурують в ТД-описах макросистеми, оскільки внутрішня структура системи не розглядається в принципі.
Термодинамічні аксіоми (закони ТД) можна отримати в межах статистичного підходу статистичної фізики, отже, статистичний підхід є більш загальним і здатним обґрунтувати всю ТД. Глибинний імовірнісний характер законів ТД взагалі можна виявити лише в межах СФ, її статистичного методу. Будь-яка статистична теорія, завданням якої є з’єднати мікро- та макропараметри великої системи, повинна підкорятися наступним простим вимогам:
Ï переважну частину мікроскопічної інформації про систему можна зігнорувати, аби не мати справи з надмірною кількістю мікроскопічних параметрів, котрі характеризують рух та взаємодію мікрочастинок системи;
Ï проте, необхідно утримати деяку мінімальну частину мікроскопічної інформації відносно мікрочастинок, яка б дозволяла оцінювати будь-які макропараметри для всієї великої системи, як цілого
Ï часова причинність, котра керує мікропроцесами на мікрорівні, не повинна проявлятися на макрорівні;
Ï закони термодинаміки повинні отримати зрозуміле мікроскопічне обґрунтування;
Якщо розглядати статистичну фізику як теорію мікропроцесів у великих системах, то викладені вище вимоги є завданнями статистичної фізики, як такої теорії.
Під час вивчення макросистеми в статистичній фізиці завжди спираються на певну модель системи на її мікрорівні. Спочатку визначають структурні одиниці макросистеми (молекули, атоми, іони, тощо). Далі з’ясовують в який спосіб ці одиниці взаємодіють поміж собою і яким шляхом описувати їх рух: з точки зору класичної, чи, можливо, з позицій квантової механіки.
Загальне припущення про рух мікрочастинок полягає в його стохастичності, тобто випадковому характері, невпорядкованості. Частинку ми розглядатимемо як матеріальну точку. Якщо вважати, що векторний імпульс (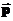 ) та векторна координата (
) та векторна координата (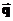 ) такої частинки одночасно мають певне значення в кожний окремий момент часу, тобто є одночасно заданими функціями часу, то таке припущення відповідає класичному (неквантовому) підходу. Як векторна координата, так і векторний імпульс частинки мають три скалярні (не обов’язково декартові) компоненти. Одночасне завдання
) такої частинки одночасно мають певне значення в кожний окремий момент часу, тобто є одночасно заданими функціями часу, то таке припущення відповідає класичному (неквантовому) підходу. Як векторна координата, так і векторний імпульс частинки мають три скалярні (не обов’язково декартові) компоненти. Одночасне завдання 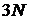 координат, та
координат, та 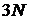 імпульсів повністю визначає мікроскопічний стан системи (мікростани). Це, умовно кажучи, детальний мікроскопічний рівень інформації про систему, яка має
імпульсів повністю визначає мікроскопічний стан системи (мікростани). Це, умовно кажучи, детальний мікроскопічний рівень інформації про систему, яка має 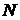 статистично незалежних одна від одної частинок.
статистично незалежних одна від одної частинок.
Макроскопічний стан системи описується невеликою кількістю макропараметрів (енергія системи, її сумарний векторний імпульс, температура, тиск, об’єм, густина, тощо). Такі параметри характеризують не окрему мікрочастинку, а систему загалом. Вони “малюють крупноплановий портрет” системи, без зайвих дрібних деталей.
Мікростани системи безперервно змінюють один іншого, хоча б тому, що кожна координата і кожен імпульс для кожної мікрочастинки залежать від часу: 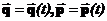 згідно із законом руху кожної частинки. Перенумеруємо скалярні компоненти координат та імпульсів індексом
згідно із законом руху кожної частинки. Перенумеруємо скалярні компоненти координат та імпульсів індексом 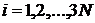 .
.
Під символами 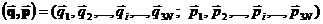 надалі розумітимемо сукупність всіх
надалі розумітимемо сукупність всіх 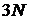 - координат та всіх
- координат та всіх 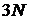 - імпульсів системи статистично незалежних частинок.
- імпульсів системи статистично незалежних частинок.
Макростан системи, проте, навіть при безупинній та стохастичній зміні її мікростанів, може лишатися незмінним в часі, сталим та однорідним: тоді зокрема матимемо, що 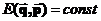 . Кількість різних мікростанів, які є сумісними з одним і тим самим рівноважним макростаном називатимемо статистичною вагою макростану
. Кількість різних мікростанів, які є сумісними з одним і тим самим рівноважним макростаном називатимемо статистичною вагою макростану 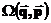 . Чим більшою є статистична вага макрос тану, чим більшою кількістю мікростанів він може бути забезпечений, тим більшою є статистична ймовірність такого макростану. Припустимо, що для мікро станів з енергіями макростанів
. Чим більшою є статистична вага макрос тану, чим більшою кількістю мікростанів він може бути забезпечений, тим більшою є статистична ймовірність такого макростану. Припустимо, що для мікро станів з енергіями макростанів 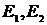 статистичні ваги є різними:
статистичні ваги є різними: 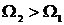 . В такому разі ймовірність того, що система перебуває в стані з енергією
. В такому разі ймовірність того, що система перебуває в стані з енергією 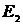 є вищою.
є вищою.
Ймовірність будь-якого мікростану з набору мікростанів, що відповідають одному й тому самому макростанові, є однаковою. Це твердження в статистичній фізиці відомо як теорема про рівноймовірність мікростанів. Ймовірності ж макростанів визначаються їх статистичними вагами.
Є принципово два різних способи експериментального дослідження ймовірностей (отже, й статистичних ваг) різних можливих для системи макростанів. Перший з них полягає в довготривалому спостереженні за однією великою системою 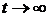 . Припустимо, що
. Припустимо, що 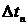 - сумарний час, який система за час спостереження перебувала в одному з
- сумарний час, який система за час спостереження перебувала в одному з 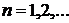 можливих макростанів системи. Тоді ймовірність певного макростану є:
можливих макростанів системи. Тоді ймовірність певного макростану є:
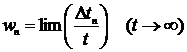
| (1) |
Інший спосіб полягає у спостереженні за великою кількістю 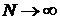 абсолютно однакових в початковий момент часу, але статистично незалежних одна від одної систем (ансамблем Гіббса). Кожна така система змінює свої стани незалежно від інших і через певний невеликий проміжок часу можна підрахувати кількість систем
абсолютно однакових в початковий момент часу, але статистично незалежних одна від одної систем (ансамблем Гіббса). Кожна така система змінює свої стани незалежно від інших і через певний невеликий проміжок часу можна підрахувати кількість систем 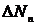 ,які потрапили в той чи інший стан. Ймовірність в такому методі знаходимо як:
,які потрапили в той чи інший стан. Ймовірність в такому методі знаходимо як:
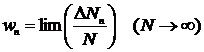
| (2) |
Зміст так званої ергодичної гіпотези статистичної фізики полягає в тому, що вона вважає ймовірності (1) та (2) абсолютно однаковими.
Кожна з них може бути використана для знаходження середніх по всіх можливих макростанах системи параметрів. Припустимо, що 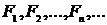 -низка значень певного макропараметри для різних макростанів системи. Тоді середнім значенням макропараметри
-низка значень певного макропараметри для різних макростанів системи. Тоді середнім значенням макропараметри 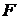 для системи як цілого вважають його математичне очікування:
для системи як цілого вважають його математичне очікування:
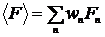
| (3) |
Абсолютною флуктуацією макропараметра 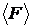 (3) називають величину:
(3) називають величину:
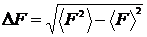
| (4) |
яка є квадратним коренем з середнього квадрату макропараметри за відрахуванням квадрату його середнього значення.
ü ГОЛОВНІ ПОСТУЛАТИ МКТ. ПОНЯТТЯ ІДЕАЛЬНОГО ГАЗУ
Кількістю ступенів свободи системи частинок 
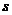 називають кількість незалежних координат, які потрібно вказати для повного опису конфігурації системи. Якщо система складається з
називають кількість незалежних координат, які потрібно вказати для повного опису конфігурації системи. Якщо система складається з 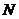 частинок, і кожна частинка є незалежною від інших, то така система потребує для свого опису
частинок, і кожна частинка є незалежною від інших, то така система потребує для свого опису 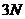 координат:
координат: 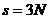 . Зокрема, кількість степенів свободи для найпростішої системи, що складається з однієї окремої частинки
. Зокрема, кількість степенів свободи для найпростішої системи, що складається з однієї окремої частинки 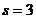 . Проте, часто в системах спостерігаються різного типу зв’язки поміж координатами частинок: припустимо, що наша частинка змушена рухатися по деякій площині, і тому на три її координати накладена умова (зв’язок) наступного вигляду:
. Проте, часто в системах спостерігаються різного типу зв’язки поміж координатами частинок: припустимо, що наша частинка змушена рухатися по деякій площині, і тому на три її координати накладена умова (зв’язок) наступного вигляду:
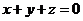
| (5) |
Отже, не всі три координати частинки є незалежними: якщо ми вільно обрали дві з них (припустимо 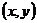 ), то третя координата автоматично знаходиться з (2.1.5) як
), то третя координата автоматично знаходиться з (2.1.5) як 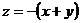 , тобто третя координата є залежною від перших двох. Отже, кількість ступенів свободи в системах, де існують зв’язки поміж координатами частинок є меншою:
, тобто третя координата є залежною від перших двох. Отже, кількість ступенів свободи в системах, де існують зв’язки поміж координатами частинок є меншою:
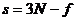
| (6) |
де 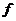 - кількість зв’язків поміж координатами частинок системи.
- кількість зв’язків поміж координатами частинок системи.
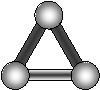
Розглянемо з цієї точки зору молекули з різною кількістю атомів (табл.2.1.1)
| Граф молекули | 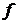
| 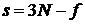
|

| |||
| |||
3, 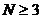
| 
|
Примітка: для чотирьохатомних молекул маємо 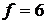 , отже,
, отже, 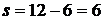 , як і для трьохатомних. Звідси заключаємо, що
, як і для трьохатомних. Звідси заключаємо, що 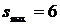 для
для 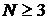 .
.
Молекулярно-кінетична теорія (МКТ) є спрощеним варіантом статистичної фізики у застосуванні до газів та парів. Головні постулати МКТ нічим не відрізняються від головних ідей статистичної фізики. Якщо застосувати їх до газів, то можна сформулювати наступні положення:
Ï всі гази складаються з мікрочастинок (атомів, іонів, молекул, тощо), які перебувають в хаотичному, безупинному русі;
Ï поміж частинками можливі зіткнення (колізії), під час яких частинки змінюють напрям руху, у той час як від зіткнення до зіткнення частинки рухаються прямолінійно.
Всі гази та пари є чимось подібними один до одного, зокрема можна вказати на такі спільні риси газів при звичайних, не екстремальних, зовнішніх умовах (помірному тискові та температурі):
Ï Власні розміри мікрочастинок набагато менші середньої відстані поміж частинками
Ï
Ï Частинки відносно слабо взаємодіють на відстані, причому чим більша середня відстань поміж частинками тим взаємодія слабкіша
Ï При зіткненні поміж собою, або зі стінками ємності, в якій вони знаходяться, частинки суттєво змінюють напрям руху (напрям своїх векторів імпульсів), однак вони практично не змінюють модулів своїх векторів імпульсів – тобто їх зіткнення майже пружні.
Така спільність загальних властивостей всіх газів дозволяє ввести у розгляд модель так званого ідеального газу, в якому наведені вище риси поведінки реальних газів доведені до абсолюту. Отже, ідеальний газ це газ матеріальних точок, які не взаємодіють поміж собою на відстані, а при зіткненнях ведуть себе як пружні кулі.
ü  ОСНОВНЕ РІВНЯННЯ МОЛЕКУЛЯРНО-КІНЕТИЧНОЇ ТЕОРІЇ ТА РІВНЯННЯ МЕНДЕЛЄЄВА-КЛАПЕЙРОНА
ОСНОВНЕ РІВНЯННЯ МОЛЕКУЛЯРНО-КІНЕТИЧНОЇ ТЕОРІЇ ТА РІВНЯННЯ МЕНДЕЛЄЄВА-КЛАПЕЙРОНА
Припустимо, що в кубічній ємності, зображеній на Мал.2.1.1, знаходяться 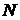 молекул ідеального газу. Розглянемо зіткнення молекули із стінкою, що перпендикулярна осі
молекул ідеального газу. Розглянемо зіткнення молекули із стінкою, що перпендикулярна осі 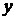 . Молекула при такому зіткненні передає стінці певний імпульс. Якщо зіткнення, як ми припустили, є пружнім, то:
. Молекула при такому зіткненні передає стінці певний імпульс. Якщо зіткнення, як ми припустили, є пружнім, то:
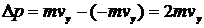
| (7) |
Час перегону молекули від стінки до стінки і назад дорівнює 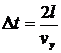 , де
, де 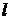 - ребро куба (відстань поміж стінками). Отже сила, з якою молекула діє на стінку дорівнює:
- ребро куба (відстань поміж стінками). Отже сила, з якою молекула діє на стінку дорівнює:
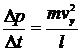
| (8) |
В напрямі осі 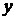 рухається третина всіх молекул, тобто повна сила повинна бути в
рухається третина всіх молекул, тобто повна сила повинна бути в 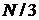 разів більша, а замість величини
разів більша, а замість величини 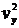 для конкретної молекули, ми повинні взяти середню величину
для конкретної молекули, ми повинні взяти середню величину 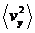 для всіх цих молекул:
для всіх цих молекул:
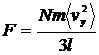
| (9) |
Тиск отримаємо, якщо силу поділимо на площу стінки, тобто на 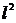 :
:
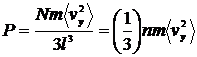
| (10) |
де через 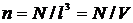 позначено концентрацію молекул (кількість молекул на одиницю об’єму). Останню формулу неважко переписати у вигляді:
позначено концентрацію молекул (кількість молекул на одиницю об’єму). Останню формулу неважко переписати у вигляді:
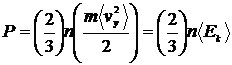
| (11) |
де через 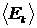 позначено середню кінетичну енергію газу (оскільки потенційна енергія взаємодії молекул в ідеальному газі дорівнює нулю, то це також і середня повна енергія молекули). Рівняння (11) є однією з форм головного рівняння МКТ для газів.
позначено середню кінетичну енергію газу (оскільки потенційна енергія взаємодії молекул в ідеальному газі дорівнює нулю, то це також і середня повна енергія молекули). Рівняння (11) є однією з форм головного рівняння МКТ для газів.
Дійсно 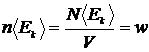 - густина енергії (кількість енергії на одиницю об’єму). Отже:
- густина енергії (кількість енергії на одиницю об’єму). Отже:
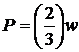
| (12) |
Тиск в ідеальному газі, як видно з (12), прямо пропорційний густині енергії, яка в свою чергу прямо пропорційна добутку концентрації на середню кінетичну енергію однієї молекули.
Введемо нову величину, абсолютну температуру 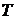 , через співвідношення:
, через співвідношення:
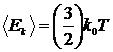
| (13) |
 де
де 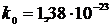 Дж/К – стала Больцмана. З (13) видно, що температура є мірою середньої кінетичної енергії: якщо зростає інтенсивність руху молекул, то зростає середня кінетична енергія молекули, разом з нею зростає і температура. Вірно й навпаки: зростання температури означає також обов’язкове збільшення середньої кінетичної енергії молекул.
Дж/К – стала Больцмана. З (13) видно, що температура є мірою середньої кінетичної енергії: якщо зростає інтенсивність руху молекул, то зростає середня кінетична енергія молекули, разом з нею зростає і температура. Вірно й навпаки: зростання температури означає також обов’язкове збільшення середньої кінетичної енергії молекул.
Для вимірювання температури користуються різними фізичними ефектами: найчастіше ефектом теплового розширенням речовин із підвищенням температури (термометри). Існують різні шкали температур (Кельвіна, Цельсія, Фаренгейта, Реомюра, тощо). В Європі, зокрема, поширеною є шкала Цельсія, яка відрізняється від абсолютної температури за шкалою Кельвіна лише початком відліку: нулю за Цельсієм відповідає абсолютна температура 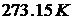 :
: 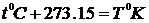 .
.
Зв’язок поміж тиском та температурою в ідеальному газі:
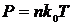
| (14) |
Отже тиск в ідеальному газі зростає з температурою, він також зростає при збільшенні концентрації молекул.
Рівняння (15) неважко привести к вигляду, відомому як рівняння Мендєлєєва-Клапейрона. Дійсно, виходячи з того, що 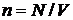 , можна отримати
, можна отримати
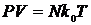
| (15) |
помноживши та поділивши праву частину на число Авогадро і приймаючи до уваги що 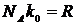 , де
, де 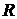 - так звана універсальна газова стала, маємо, що:
- так звана універсальна газова стала, маємо, що:
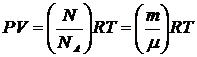
| (16) |
Останнє рівняння відомо в МКТ як рівняння стану ідеального газу, або рівняння Мендєлєєва-Клапейрона. Воно пов’язує три параметра ідеального газу (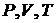 ), з яких незалежними є лише будь-яка пара параметрів, а третій параметр визначається з рівняння (17). Під
), з яких незалежними є лише будь-яка пара параметрів, а третій параметр визначається з рівняння (17). Під 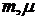 треба розуміти відповідно масу газу та масу одного кіломоля газу:
треба розуміти відповідно масу газу та масу одного кіломоля газу: 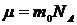 ,
, 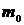 -маса окремої молекули. Отже під кіломолем треба розуміти одиницю кількості молекул, яка дорівнює числу Авогадро
-маса окремої молекули. Отже під кіломолем треба розуміти одиницю кількості молекул, яка дорівнює числу Авогадро 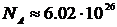 .
.
ü РЕАЛЬНІ ГАЗИ. РІВНЯННЯ ВАН-ДЕР-ВААЛЬСА
Рівняння (16) є справедливим доти, доки є коректними наші припущення щодо ідеальності газу. Наприклад, при високій густині газу вже не можна нехтувати власними розмірами молекул порівняно з відстанню поміж ними, оскільки вони стають порівняльними поміж собою. Окрім того в реальних газах завжди існує додатковий до зовнішнього (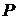 ) більший, або менший тиск (
) більший, або менший тиск (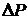 ), який пов’язаний із слабкою, але існуючою в реальних газах взаємодією поміж молекулами.
), який пов’язаний із слабкою, але існуючою в реальних газах взаємодією поміж молекулами.
Одним з найпростіших рівнянь стану для реальних газів є так зване рівняння Ван-дер-Ваальса. В цьому рівнянні:
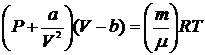
| (17) |
де ми бачимо дві константи (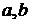 ), котрі описують конкретний реальний газ і наводяться в таблицях фізичних констант для різних газів.
), котрі описують конкретний реальний газ і наводяться в таблицях фізичних констант для різних газів.
Константа 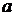 пов’язана із згаданим додатковим тиском:
пов’язана із згаданим додатковим тиском: 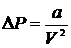 , тоді як константа
, тоді як константа 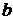 враховує власний об’єм всіх молекул: величина
враховує власний об’єм всіх молекул: величина 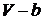 є об’ємом, доступним для молекул реального газу.
є об’ємом, доступним для молекул реального газу.
Додатковий тиск 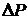 в реальних газах виникає за рахунок слабкої взаємодії поміж молекулами, якою нехтують для ідеального газу. Сили взаємодії з боку молекул оточення взаємно компенсують одна одну для будь-якої молекули в об’ємі реального газу внаслідок симетрії їх розташування. Втім для молекул на межі газу з іншим середовищем це не так: сили взаємодії з молекулами газу не компенсують сили взаємодії з оточуючим середовищем. Результатом є виникнення поверхневих сил, нормальних до межі газ-оточуюче середовище. Саме вони створюють додатковий тиск в реальному газі.
в реальних газах виникає за рахунок слабкої взаємодії поміж молекулами, якою нехтують для ідеального газу. Сили взаємодії з боку молекул оточення взаємно компенсують одна одну для будь-якої молекули в об’ємі реального газу внаслідок симетрії їх розташування. Втім для молекул на межі газу з іншим середовищем це не так: сили взаємодії з молекулами газу не компенсують сили взаємодії з оточуючим середовищем. Результатом є виникнення поверхневих сил, нормальних до межі газ-оточуюче середовище. Саме вони створюють додатковий тиск в реальному газі.
Якщо припустити, що 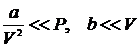 , тобто знехтувати виправленнями Ван-дер-Ваальса, то рівняння Ван-дер-Ваальса (17) переходить в рівняння Мендєлєєва-Клапейрона (17) для ідеального газу. Варто також зауважити, що рівняння Менделєєва-Клапейрона є лінійним рівнянням відносно об’єму газу
, тобто знехтувати виправленнями Ван-дер-Ваальса, то рівняння Ван-дер-Ваальса (17) переходить в рівняння Мендєлєєва-Клапейрона (17) для ідеального газу. Варто також зауважити, що рівняння Менделєєва-Клапейрона є лінійним рівнянням відносно об’єму газу 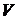 , у той час як рівняння Ван-дер-Ваальса – кубічним, що стає особливо наочним, якщо переписати його у вигляді:
, у той час як рівняння Ван-дер-Ваальса – кубічним, що стає особливо наочним, якщо переписати його у вигляді:
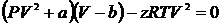
| (18) |
де 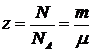 - кількість кіломолей газу.
- кількість кіломолей газу.
 2017-12-14
2017-12-14 662
662






