Лекція 8
Багатокрокові методи розв’язання
диференційних рівнянь
Методи Ейлера, Гюна, Тейлора, Рунге-Кута називаються однокроковими методами, тому що в них використовується лише інформація про значення диференційного рівняння в одній попередній точці для того, щоб обрахувати значення в наступній, тобто лише значення в початковій точці (t 0; y 0) використовується для обчислення значення диференційного рівняння в точці (t 1; y 1), і загалом, щоб обрахувати ук +1 необхідне лише ук. Але після знаходження значень диференційного рівняння в декількох точках можна їх використовувати для отримання більш точних результатів у наступній вузловій точці. Наприклад, для чотирикрокового методу Адамса-Бешфорса-Маултона необхідні значення в точках ук -3, ук -2, ук -1, та ук для обчислення ук +1. У цьому методі значення диференційного рівняння в чотирьох початкових точках, (t 0, y 0), (t 1, y 1), (t 2, y 2) та (t 3, y 3), розраховуються спочатку для подальшої генерації точок {(t k, y k): k 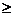 4} з використанням багатокрокового методу.
4} з використанням багатокрокового методу.
Корисною властивістю багатокрокового методу є можливість визначити локальну помилку відсікання (ЛПВ) та ввести корегуючий елемент, який підвищує точність відповіді на кожному кроці. Також можна визначити, чи буде довжина кроку достатньою, щоб отримати значення ук+1 із заданим рівнем точності, або задати більший крок, який виключить непотрібні обрахування і забезпечить необхідну точність розрахунків.
Метод Адамса-Бешфорса-Маултона. Метод прогнозу-корекції Адамса-Бешфорса-Маултона – це багатокроковий метод, виведений із фундаментальної теореми аналізу:
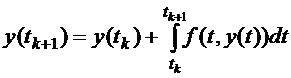 . (8.1)
. (8.1)
Прогноз використовує наближення поліномом Лагранжа для функції f (t, y (t)), що побудована по точках (tk -3, yk -3), (tk -2, yk -2), (tk -1, yk -1) i (tk, yk). Для функції f (t, y (t)) з формули (8.1), яка інтегрується на інтервалі [ tk, tk +1] прогноз Адамса-Бешфорса, має вигляд

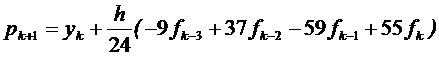 . (8.2)
. (8.2)
Як будь-який прогноз, він потребує корекції. Коректор отримується аналогічно. А саме, як тільки значення pk +1 обраховано, його використовують для побудови наступного поліному Лагранжа для функції f (t, y (t)), який будується по точкам (tk -2; yk -2), (tk -1; yk -1) (tk; yk) і новій точці (tk +1; yk +1), в якій замість yk +1 використовується прогноз pk +1, тобто функція в точці tk +1; обраховується як f (tk +1, pk +1). Після розрахунку поліному шляхом інтегрування на інтервалі [ tk; tk +1] отримаємо коректор Адамса-Маултона:


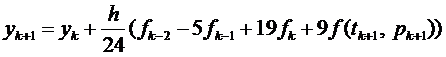 . (8.3)
. (8.3)
Оцінка помилки і корекція. Залишковий елемент формули чисельного інтегрування використовується, щоб отримати і прогноз, і коректор порядку О(h 5). Локальна помилка відсікання для формул (8.2) та (8.3) має вигляд:
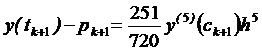 , (локальна похибка відсікання для прогнозу) (8.4)
, (локальна похибка відсікання для прогнозу) (8.4)
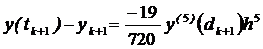 . (локальна похибка відсікання для коректора) (8.5)
. (локальна похибка відсікання для коректора) (8.5)
Припустимо, що h мале і y (5) (t) – майже усталена на інтервалі. Тоді можна виключити члени, що містять похідну 5-го порядку у формулах (8.4) та (8.5). В результаті отримаємо:
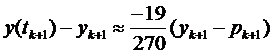 . (8.6)
. (8.6)
Переваги методу прогнозу-корекції Адамса-Бешфорса-Маултона у тому, що формула (8.6) дає наближену оцінку помилки, яку отримуємо при обчисленні значень pk +1 i yk +1, не використовуючи у (5)(t).
Коректор (8.3) використовує наближення 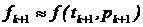 при обчисленні ук +1. Оскільки ук +1 також є оцінкою для у (tk +1), її можна використовувати у коректорі (8.3) для генерування нового наближення для fk +1, яке, в свою чергу, буде генерувати нове значення для ук +1. Окрім того, якщо продовжити цю ітерацію у коректорі, вона буде збігатись до фіксованої точки у формулі (8.3) швидше, ніж при класичному розв‘язку диференційного рівняння. Якщо необхідно підвищити точність, то процедура корекції більш ефективна, ніж зменшення довжини кроку.
при обчисленні ук +1. Оскільки ук +1 також є оцінкою для у (tk +1), її можна використовувати у коректорі (8.3) для генерування нового наближення для fk +1, яке, в свою чергу, буде генерувати нове значення для ук +1. Окрім того, якщо продовжити цю ітерацію у коректорі, вона буде збігатись до фіксованої точки у формулі (8.3) швидше, ніж при класичному розв‘язку диференційного рівняння. Якщо необхідно підвищити точність, то процедура корекції більш ефективна, ніж зменшення довжини кроку.
Формулу (8.6.) можна використовувати для покращення значень прогнозу. Якщо припустити, що різниця між значеннями прогнозу і корекції на кожному кроці змінюється повільно, то можна підставити 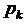 і
і 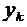 замість
замість 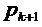 і
і 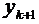 в (8.6) і отримати наступний управляючий параметр:
в (8.6) і отримати наступний управляючий параметр:


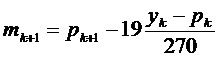 (8.7)
(8.7)
Його значення використовується замість 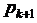 на кроці корекції, і формула (8.3) приймає вигляд:
на кроці корекції, і формула (8.3) приймає вигляд:
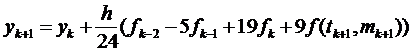 (8.8)
(8.8)
Формулу (8.6) також можна використовувати для визначення адаптивної довжини кроку. Можливо зменшити довжину кроку, наприклад, до h /2 і збільшити до 2 h. Припустимо ε = 5x10-6 – критерій відносної похибки, і нехай kε = 10-5
Якщо 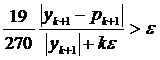 , тоді h = h /2 (8.9)
, тоді h = h /2 (8.9)
Якщо 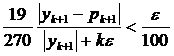 , тоді h =2 h (8.10)
, тоді h =2 h (8.10)
Якщо прогноз і корекція значень не дають відповідностей розв‘язків у п’ять значущих цифр, то за формулою (8.9) зменшують довжину кроку. Якщо ж розв‘язки збігаються до семи або більше значущих цифр, то за формулою (8.10) довжина кроку збільшується.
Зменшення довжини кроку потребує чотирьох нових початкових значень. Для заміщення значень, яких не вистачає і які ділять інтервали [ tk -2, tk -1] і [ tk -1, tk ] навпіл, використаємо інтерполяцію функції f (t,y (t)) поліномом четвертого ступеню. Нові чотири вузлові точки, tk -3/2, tk -1, tk -1/2 і tk, використовуються в наступних розрахунках.
Інтерполяційна формула, необхідна для отримання нових початкових значень (рис. 8.1) для кроку h/2 має вигляд:
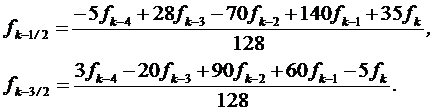 (8.11)
(8.11)

Рис. 8.1. Зменшення довжини кроку до h /2.
Набагато простіше збільшити довжину кроку, тоді для розрахунків за одно-кроковим методом потрібно розрахувати сім попередніх точок (рис. 8.2), щоб подвоїти крок.

Рис. 8.2. Збільшення довжини кроку до 2 ∙ h.
Метод Мілна-Сімпсона. Інший розповсюджений метод прогнозу-корекції це метод Мілна-Сімпсона. Його прогноз базується на інтегруванні функції f (t, y (t)) на інтервалі [ tk -3, fk +1]:
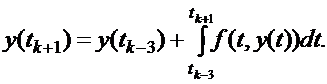 (8.12)
(8.12)
Прогноз використовує наближення поліномом Лагранжа для f(t, y(t)), побудований по точкам (tk -3, fk -3), (tk -2, fk -2), (tk -1, fk -1) та (tk, fk). Інтегруємо його по інтервалу [ tk -3, fk +1] і отримуємо прогноз Мілна:

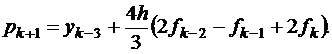 (8.13)
(8.13)
Коректор отримуємо аналогічно. На цьому етапі використаємо значення pk +1. Будуємо інший поліном Лагранжа для функції f (t, y (t)) по точках (tk -1, fk- 1), (tk, fk) і у новій точці (tk +1, fk +1) = (tk +1, f (tk +1, pk +1)). Інтегруємо поліномом на відрізку [ t k -1, tk +1] і в результаті отримаємо відому формулу Сімпсона:

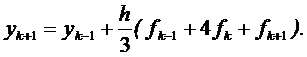 (3.14)
(3.14)
Оцінка помилка та корекція. Залишковий член формули чисельного інтегрування використовується для отримання як прогнозу, так і коректору порядку О(h 5). Остаточна загальна помилка (О.З.П.) для формул (8.13) та (8.14) дорівнює
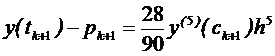 (О.З.П. для прогнозу) (8.15)
(О.З.П. для прогнозу) (8.15)
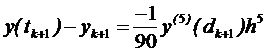 (О.З.П. для коректора) (8.16)
(О.З.П. для коректора) (8.16)
Припустимо, що крок h настільки малий, що y (5)(t) майже стала на інтервалі 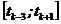 . Тоді із формул (8.15) і (8.16) можемо виключити елементи, які містять похідну п’ятого порядкую, і в результаті отримати формулу:
. Тоді із формул (8.15) і (8.16) можемо виключити елементи, які містять похідну п’ятого порядкую, і в результаті отримати формулу:
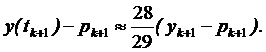 (8.17)
(8.17)
Формула (3.17) дає оцінку прогнозу, яка ґрунтується на обчисленні значень 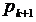 і
і 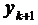 і не використовує
і не використовує 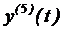 . Її можна застосовувати для покращення значень прогнозу. Якщо припустити, що різниця між значеннями прогнозу
. Її можна застосовувати для покращення значень прогнозу. Якщо припустити, що різниця між значеннями прогнозу 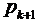 і корекції
і корекції 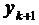 на кожному кроці змінюється повільно, то можна підставити
на кожному кроці змінюється повільно, то можна підставити 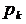 і
і 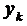 замість
замість 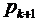 і
і 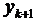 в формулу (8.17) і отримати наступний управляючий параметр:
в формулу (8.17) і отримати наступний управляючий параметр:

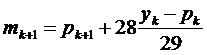 (8.18)
(8.18)
Його значення використовується замість 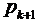 на кроці корекції, і формула (8.14) приймає вигляд:
на кроці корекції, і формула (8.14) приймає вигляд:
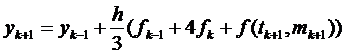 (8.19)
(8.19)
Таким чином, в покращеному модифікованому методі Мілна-Сімпсона послідовно використовуються наступні формули:


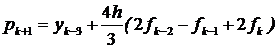 (прогноз)
(прогноз)




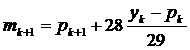 (управляючий параметр)
(управляючий параметр)
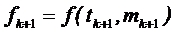

 (8.20)
(8.20)



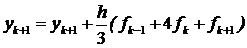 (коректор)
(коректор)
Метод Хеммінга. Ще один важливий метод для розв’язання задачі Коші y’=f(t,y) з початковою умовою y(a)=y0 на інтервалі [a, b] – метод Хеммінга. Прогноз, як і в попередніх методах, базується на наближенні поліномом Лагранжа для f(t, y(t)). Він побудований по точкам (tk -3, fk -3), (tk -2, fk -2), (tk -1, fk -1) та (tk, fk). При інтегруванні отримуємо прогноз Хеммінга:

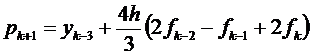 (8.21)
(8.21)
Управляючий параметр:

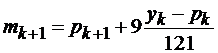 (8.22)
(8.22)
Коректор отримуємо, будуючи другий поліном Лагранжа для функції f (t, y (t)) по точках (tk -1, fk- 1), (tk, fk) і у новій точці (tk +1, fk +1) = (tk +1, f (tk +1, pk +1)). В результаті одержуємо формулу:

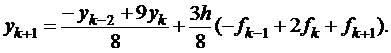 (8.23)
(8.23)
Методи прогнозу корекції при великому кроці розрахунку можуть бути не стійкими. При таких розрахунках похибка ітерації збільшується від кроку до кроку, що і обумовлює нестійкість. Для забезпечення стійкості розглянутих методів потрібно корегувати крок на етапі його вибору. З умови стійкості метод крок вибирається за нерівностями:

 (8.24)
(8.24)
Методи Адамса-Бешфорса-Мултона і Хемінга дозволяють отримати результати з високим рівнем точності за невелику кількість кроків, тобто швидко збігаються до розв‘язку.
Наведемо приклад розв‘язання задачі Коші для рівняння 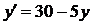 з початковими умовами y(0) = 1 на інтервалі [0;10]. Всі три розглянуті вище багатокрокові методи мають порядок похибки розв‘язку О(h5). Побудуємо графіки розв‘язків рівняння при мінімальній (меншій за визначений за критерієм стійкості методу) кількості кроків і при кількості кроків, визначеній за формулами (8.24).
з початковими умовами y(0) = 1 на інтервалі [0;10]. Всі три розглянуті вище багатокрокові методи мають порядок похибки розв‘язку О(h5). Побудуємо графіки розв‘язків рівняння при мінімальній (меншій за визначений за критерієм стійкості методу) кількості кроків і при кількості кроків, визначеній за формулами (8.24).

 Для методу Адамса-Бешфорса-Маултона
Для методу Адамса-Бешфорса-Маултона 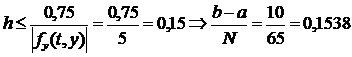 ; тому N = 65 (рис. 8.3). *// У прикладі
; тому N = 65 (рис. 8.3). *// У прикладі 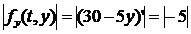
Для методу Мілна-Сімпсона 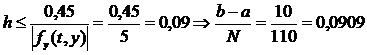 ; тому N = 110 (рис. 8.4).
; тому N = 110 (рис. 8.4).
Для методу Хемінга 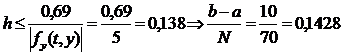 ; тому N = 70 (рис. 8.5).
; тому N = 70 (рис. 8.5).
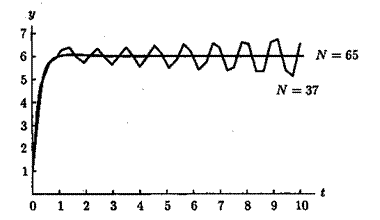
Рис. 8.3. Розв‘язок задачі за методом Адамса-Бешфорса-Маултона.
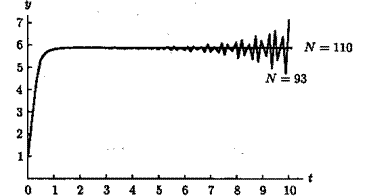
Рис. 8.4. Розв‘язок задачі за методом Мілна-Сімпсона.
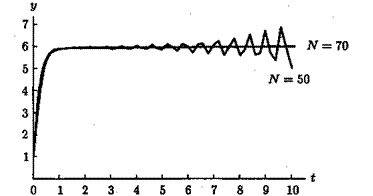
Рис. 8.5. Розв‘язок задачі за методом Хемінга.
 2017-12-14
2017-12-14 468
468






