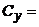 999,60 999,60 |  = 19 = 19 |  67793,28 67793,28 |  66793,68 66793,68 | |
 835,36 835,36 |  = 4 = 4 | 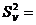 208,84 208,84 |  19,07 > 19,07 > |  3,06 3,06 |
 44,17 44,17 |  = 3 = 3 |  14,72 14,72 |  1,47 < 1,47 < |  3,49 3,49 |
 120,07 120,07 | 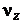 = 12 = 12 |  10,01 10,01 | ||
 164,24 164,24 |  = 15 = 15 | 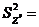 10,95 10,95 |  4,98 4,98 | ц/га (8,6 %) |
II. Вычислить общее варьирование результатов эксперимента Су и его степени свободы  :
:
 = 46,52 +... + 61,32 – 66793,68 = 67793,28 – 66793,68 = 999,60
= 46,52 +... + 61,32 – 66793,68 = 67793,28 – 66793,68 = 999,60

III. Вычислить варьирование по вариантам Сv, его степени свободы  v и дисперсию
v и дисперсию 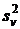 :
:
 = (194,32 +... + 239,12): 4 – 66793,68 = 835,36
= (194,32 +... + 239,12): 4 – 66793,68 = 835,36
 v = l – 1 = 5 – 1 = 4
v = l – 1 = 5 – 1 = 4
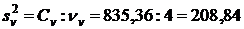
IV. Вычислить варьирование по повторениям Ср, его степени свободы  р и дисперсию
р и дисперсию 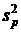 :
:
 = (279,52 +... + 291,32): 5 – 66793,68 = 44,17
= (279,52 +... + 291,32): 5 – 66793,68 = 44,17


V. Вычислить случайное варьирование Сz, его степени свободы  z и дисперсию
z и дисперсию 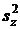 :
:
Cz = Cy – Cv – Cp = 999,60 – 835,36 – 44,17 = 120,07
 z =
z =  y -
y -  v -
v -  p = 19 – 4 – 3 = 12
p = 19 – 4 – 3 = 12
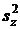 = C z:
= C z:  z = 120,07: 12 = 10,01
z = 120,07: 12 = 10,01
VI. Вычислить эф повторений Fp, по специальным таблицах (в приложении 2 методического пособия или в учебнике Б.А.Доспехова на стр. 318) найти критерий Фишера для повторений Fa(P) и по результатам их сравнения, во-первых, определить вид варьирования условий по территории опытного участка и, во вторых, адаптировать к нему модель дисперсионного анализа.
Критерий Фишера показывает, во сколько раз дисперсия по повторениям может быть больше, чем случайная дисперсия под влиянием случайных факторов, а не повторений.
В природе условия на опытном участке могут варьировать или только случайно или комбинированно, т.е. и случайно и систематически, постепенно улучшаясь по мере движения от одной к другой его стороне (см. рисунки).
  |
  |
Допустим, что на двух участках на каждой делянке будущих экспериментов убрали и взвесили урожай предшествующей культуры. Затем, используя его как ординату на вертикальной оси делянок, нанесли точки и соединили их отрезками прямой. Получится ломаная кривая. Если сглаживающая ее прямая линия располагается горизонтально, то условия на опытном участке варьировали только случайно. Повторения не будут вносить свой вклад в общее варьирование результатов, они не нужны. Если же эта линия имеет наклон, то условия на участке варьировали комбинированно, и повторения будут уменьшать погрешность эксперимента тем сильнее, чем больше наклон прямой.
Вид варьирования условий на опытном участке имеет очень большое значение для надежности выводов. Если на участках с комбинированным варьированием условий варианты распределять на делянках последовательно, то характеристика вариантов будет искаженная. Она будет содержать систематические ошибки. Ее природа видна их рисунка.
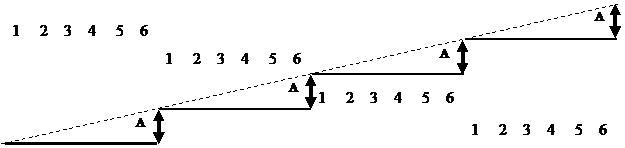
В четырех случаях из четырех шестой вариант "обеспечивает" повышение на – А ц/га по сравнению с первым. Шестой вариант будет рекомендован производству как лучший, на самом деле увеличение урожайности вызвано не 6-м вариантом, а тем, что везде он попадал на лучшую делянку. Это и есть систематическая ошибка.
Поскольку перед закладкой эксперимента вид будущего варьирования условий на опытном участке неизвестен, то повторения нужно создавать всегда. При дисперсионном анализе результатов легко определить, как варьировали условия, и решить, нужно ли воспользоваться повторениями. Для этого следует:
1. Вычислить Fp. Fp = 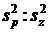 = 14,72: 10,01 = 1,47
= 14,72: 10,01 = 1,47
2. В приложении 2 или учебнике Б.А.Доспехова (на стр. 318) найти Fa(P), например, F05(P), беря в таблице по горизонтали  p, а по вертикали –
p, а по вертикали –  z. В нашем примере при
z. В нашем примере при  p = 3 и
p = 3 и  z = 12, критерий F05(P) =3,49.
z = 12, критерий F05(P) =3,49.
3. Сравнить Fp с F05(P)
Если Fp  F05(P), то: а) условия на опытном участке варьировали комбинированно, варьирование по повторениям Ср нужно оставить в модели анализа; б) дисперсионный анализ нужно завершить по VII-му шагу алгоритма.
F05(P), то: а) условия на опытном участке варьировали комбинированно, варьирование по повторениям Ср нужно оставить в модели анализа; б) дисперсионный анализ нужно завершить по VII-му шагу алгоритма.
Если Fp < F05(P), то: а) условия на опытном участке варьировали только случайно, варьирование по повторениям Ср является частью случайного варьирования Cz, б) их нужно объединить и дисперсионный анализ завершить по VIII-му и IХ-му шагам алгоритма.
В нашем примере Fp = 1,47 < F05(P) = 3,49. Значит, дисперсионный анализ завершим по VIII-му и IX-му шагам алгоритма.
Но в других экспериментах потребуется VII-й шаг, поэтому ниже приводим и его.
VII. (Использовать только при Fp > F05(P)). Определить все критерии для выводов, опираясь на vz и 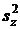 :
:
1. Вычислить F v F v = 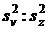
2. По тем же таблицам в приложении 2 или учебнике Б.А.Доспехова найти Fa(v), беря по горизонтали  v, а по вертикали –
v, а по вертикали –  z. Результат их сравнения использовать как обычно для формулирования выводов о вариантах (см. правила ниже).
z. Результат их сравнения использовать как обычно для формулирования выводов о вариантах (см. правила ниже).
3. Вычислить НСРа НСРa = 
Критерий Стьюдента ta находить по  z в приложении 1 или в учебнике Б.А.Доспехова (на стр. 317).
z в приложении 1 или в учебнике Б.А.Доспехова (на стр. 317).
4. Вычислить HCPa, % HCP05, %= 
VIII. (Использовать если Fp < F05(P) как в нашем примере). Вычислить истинную величину случайного варьирования результатов Сz его степени свободы  z и дисперсию
z и дисперсию 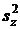 :
:
Cz = Cz + Cp = 120,07 + 44,17 = 164,24
 z =
z =  z +
z +  p = 12 + 3 = 15
p = 12 + 3 = 15
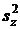 = Cz:
= Cz:  z = 164,24: 15 = 10,95
z = 164,24: 15 = 10,95
IX. (Использовать если Fp < F05(P) как в нашем примере). Определить все критерии для выводов так же, как и в VII-м шаге, но опираясь на vz' и 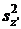 :
:
1. Вычислить F v F v =  = 208,84: 10,95 = 19,07
= 208,84: 10,95 = 19,07
2. По тем же таблицам в приложении 2 или учебнике Б.А.Доспехова найти Fa( v ), беря по горизонтали  v, а по вертикали –
v, а по вертикали –  z'. В нашем примере, при
z'. В нашем примере, при  v = 4 и
v = 4 и  z' = 15, F05( v ) =3,06. Результат их сравнения использовать как обычно для формулирования выводов о вариантах.
z' = 15, F05( v ) =3,06. Результат их сравнения использовать как обычно для формулирования выводов о вариантах.
3. Вычислить НСРа НСРa = 
Критерий Стьюдента ta находить по  z в приложении 1 или в учебнике Б.А.Доспехова (на стр. 317).
z в приложении 1 или в учебнике Б.А.Доспехова (на стр. 317).
В нашем примере, при  z' = 15, t05 = 2,13, а НСР05 =
z' = 15, t05 = 2,13, а НСР05 =  = 4,98 ц/га
= 4,98 ц/га
4. Вычислить HCPa, % HCP05, %= 
В нашем примере, HCP05, %=  = 8,6 %.
= 8,6 %.
На этом все задачи дисперсионного анализа решены, так как все критерии для выводов и рекомендаций производству уже получены.
Исходную таблицу (табл. 1) вместе с итогами дисперсионного анализа помещают в приложениях к дипломной или другой научной работы. Формулы алгоритма и вычисления по ним не приводят. Если рецензент или оппонент сомневается в итогах дисперсионного анализа, он сам должен сделать все эти вычисления, чтобы обнаружить ошибку, если она есть.
Итоговую таблицу (табл.2) вместе с выводами помещают в тексте дипломной или иной научной работы.
Итоговая таблица результатов эксперимента
Таблица 2. Влияние гербицидов на урожайность лука-севка
| Варианты | Урожайность, ц/га | Отклонения от контроля | |
| ц/га | % | ||
| Без гербицидов (контроль) | 48,6 | - | - |
| Хлоразин, 4 кг/га | 66,5 | 66,5-48,6= 17,6 | (17,6-100):48,6= 36,2 |
| Хлоразин, 8 кг/га | 52,4 | 3,8 | 7,8 |
| Рандокс, 10 кг/га | 61,6 | 13,0 | 26,7 |
| Рандокс, 15 кг/га | 59,8 | 11,2 | 23,0 |
| НСР05 | 4,98 | 8,6 | |
| Fv= 19,07 > F05 (v) = 3,06 |
Выводы:
1. Гербициды хлоразин и рандокс обеспечивают достоверное и значительной повышение урожайности лука-севка в зоне исследования.
2. Лучшая доза хлоразина составляет 4 кг/га. Увеличение ее до 8 кг снижает урожайность до уровня контроля. По-видимому, эта доза уже токсична для лука-севка.
3. Лучшая доза рандокса – 10 кг/га. Она обеспечивает такую же урожайность, как и при 15 кг, но стоимость ее в полтора раза дешевле.
4. В лучших дозах гербициды хлоразин и рандокс по влиянию на урожайность лука-севка не различаются. Следовательно, предпочтение нужно отдавать тому гербициду, у которого дешевле гектарная доза и который безопаснее для людей и природы.
Выводы и рекомендации производству формулируют с помощью логического и диалектического методов, трансформируемых в следующие принципы (приводим только самые важные из них):
1. Они должны строго соответствовать приведенным ниже правилам использования критериев F v и F05( v ), HCP05 и HCP05, %.
2. Гипотезные варианты, сравниваемые для проверки любого из трех предположений гипотезы, должны различаться только одним условием. Иначе невозможно понять, чем вызваны различия между ними.
3. Для объяснения причин различий между вариантами, не выявляемых при их сравнении по урожайности, нужно иметь результаты собственных гипотезных наблюдений. Для них тоже нужно вычислять и использовать критерии F v и F05( v ), HCP05 и HCP05, % по тем же правилам. Если таких результатов нет, а причины различий логически кажутся очевидными, то выводы нужно формулировать в предположительном виде со словами вероятно, по-видимому, очевидно и др.
4. Выводы о вариантах нужно формулировать ежегодно и по средним результатам за все годы исследований.
5. Рекомендации производству нужно формулировать только по средним данным за все годы исследований, но не менее чем за 3 года.
Раздел 4
Сравнение вариантов и формулирование выводов
При формулировании выводов и рекомендаций производству по данным проведенного дисперсионного анализа результатов эксперимента следует воспользоваться нижеприведенной таблицей.
Правила использования критериев Fv, Fa(v), HCPa, HCPa, %
при формулировании выводов и рекомендаций о вариантах эксперимента
(d – разность между вариантами; НСР05, % большая, если она превышает 12 %)
| Результат сравнения | Относительная погрешность HCPa, % | Каким должен быть вывод | ||
| Fv с Fa(v), | d c HCPa | |||
 | сравнивай варианты попарно |  | Один вариант лучше, чем другой | |
 | 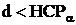 | Небольшая | Два варианта одинаковы | |
 | 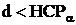 | Большая | О двух вариантах нельзя сделать достоверного вывода | |
 | говори о всех вариантах | Небольшая | Все варианты одинаковы | |
 | Большая | О всех вариантах нельзя сделать достоверного вывода | ||
| Дополнительные правила, необходимые при чтении специальной литературы: | ||||
| 1. Если автор не приводит результат сравнения Fv с Fa(v), то варианты приходится сравнивать попарно; | ||||
| 2. Если автор приводит только метрическую ошибку эксперимента и не приводит НСРa%, то ее можно вычислить самому: а) вычислить среднюю для всего эксперимента; б) метрическую ошибку разделить на эту среднюю и умножить на 100. | ||||
| 3. Если автор, не приводит ни каких критериев для сравнения, то рекомендациями по его данным пользоваться нельзя, они вряд ли подтвердятся. |
 2017-12-14
2017-12-14 1112
1112