Если отрезок [a, b] является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по формуле:
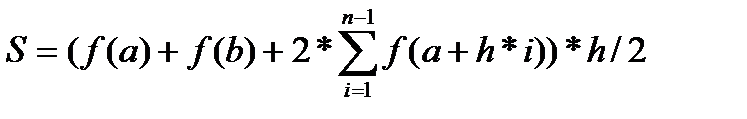
Это простое применение формулы для площади трапеции — произведение полсуммы оснований, которыми в данном случае являются значения функции в крайних точках отрезка, на высоту (длину отрезка интегрирования). (Рис. 2)
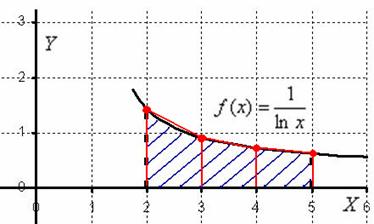
(Рис.2 Иллюстрация метода трапеции)
Метод Симпсона
В этом методе подынтегральная функция на частичном отрезке 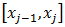 приближается параболой, проходящей через три точки
приближается параболой, проходящей через три точки 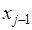
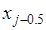
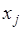 то есть интерполяционным многочленом Лагранжа второй степени:
то есть интерполяционным многочленом Лагранжа второй степени:
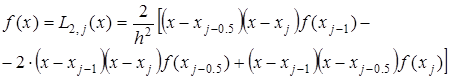
Проведя интегрирование, получим:
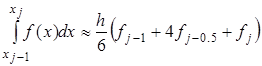
Это и есть формула Симпсона или формула парабол. На отрезке формула Симпсона примет вид:
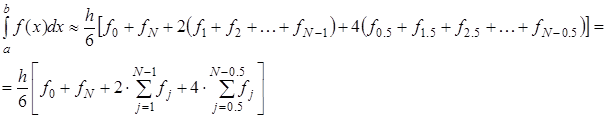
Если разбить отрезок интегрирования 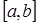 на четное количество 2N равных частей с шагом
на четное количество 2N равных частей с шагом
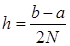 ,то можно построить параболу на каждом сдвоенном частичном отрезке
,то можно построить параболу на каждом сдвоенном частичном отрезке
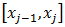 и переписать выражения (2.12-2.14) без дробных индексов. Тогда формула Симпсона примет вид:
и переписать выражения (2.12-2.14) без дробных индексов. Тогда формула Симпсона примет вид:
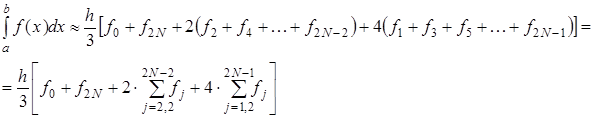
Графическое представление метода Симпсона показано на (рис.3)На каждом из сдвоенных частичных отрезков заменяем дугу данной кривой параболой.
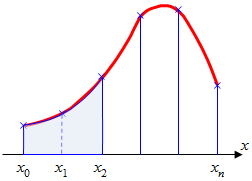 (рис.3)
(рис.3)
Метод Чебышева
Рассмотрим квадратурную формулу вида:
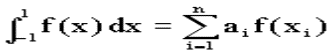
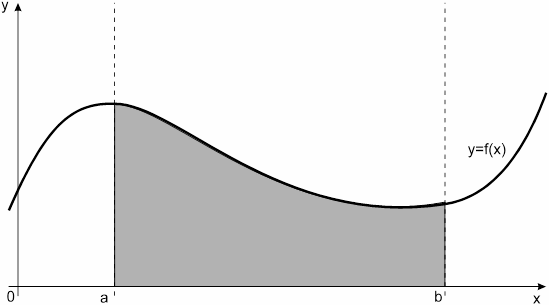
функцию f(x) будем исать в виде когда f(x) многочлен вида f(x)=ao+a1x+...+anxn. Проинтегрировав, преобразовав и подставив значения многочлена в узлах
f(x1)=a0+a1x1+a2x12+a3x13+...+anx1n
f(x2)=a0+a1x2+a2x22+a3x23+...+anx2n
f(x3)=a0+a1x3+a2x32+a3x33+...+anx3n
................
f(xn)=a0+a1xn+a2xn2+a3xn3+...+anxnn
получим формулу Чебышева.
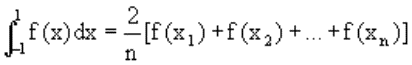
Значения х1,х2,..,хn для различных n приведены в таблице 3.
| Число интервалов n | Номер узла i | Значение узла Xi |
| 0,08375 0,312730 0,500000 0,687270 0,916249 |
(Табл.3 – Значения х1,х2,..,хn для различных n)
 2017-12-14
2017-12-14 588
588








