Практическое задание
Ткацкая фабрика производит ткань двух артикулов. Для производства 10 тыс. м2 ткани первого артикула фабрике необходимо a11 т тонковолокнистого и a21 т средневолокнистого хлопка, а для выпуска 100 тыс. м2 ткани второго артикула – соответственно, a12 и a22 т хлопка. Поставки тонковолокнистого хлопка не превышают b1 т, а средневолокнистого хлопка – b2 т.
По плану фабрика должна произвести не менее 60 тыс. м2 ткани 1-го артикула и 800 тыс. м2 ткани 2-го артикула. Прибыль фабрики от продажи 10 тыс. м2 ткани 1-го артикула составляет 1,6 тыс. руб., а от продажи 100 тыс. м2 ткани 2-го артикула – 6 тыс. руб.
Предполагая, что вся произведенная ткань будет распродана, определить оптимальный план производства ткани, обеспечивающий получение наибольшей прибыли [ 2 ].
Значения параметров aij (i = 1,2 и j = 1,2) и bj (j = 1,2) приведены в таблице 1.
Таблица 1.
| Вариант | а11 | а12 | а21 | а22 | b1 | b2 |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОГО ЗАДАНИЯ
1. Формализация задачи
Введем переменные: xi – количество выработанной ткани i-го артикула, i = 1,2, (для 1-го артикула - десятки тыс. м2, для 2-го – сотни тыс. м2).
Целевая функция (тыс. руб.) характеризует прибыль от продажи произведенной ткани двух артикулов:
F(x1, x2) = 1.6 x1 + 6 x2
Ограничения на переменные выражают лимиты на поставку сырья, а также плановые задания:
a11 x1 + a12 x2 ≤ b1
a21 x1 + a22 x2 ≤ b2
x1 ≥ 6
x2 ≥ 8
Кроме того, следует учесть неотрицательность переменных, вытекающую из их физического смысла:
xi ≥ 0, i = 1,2
Все приведенные выше зависимости носят линейный характер, поэтому данная задача представляет собой задачу линейного программирования:
F(x1, x2) = 1.6 x1 + 6 x2 → max
при a11 x1 + a12 x2 ≤ b1
a21 x1 + a22 x2 ≤ b2
x1 ≥ 6
x2 ≥ 8
xi ≥ 0, i = 1,2
2. Решение задачи
2.1. Геометрический метод решения задачи
Геометрически как целевая функция, так и границы области ограничений в системе координат переменных x1 и x2 представляют собой прямые линии [ 2 ]:
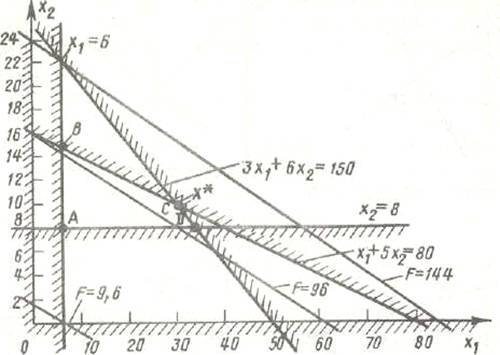
Перемещая линию целевой функции в направлении увеличения переменных до тех пор, пока хотя бы одна её точка принадлежит области допустимых значений, в точке С получим искомое оптимальное решение X* = (x1, x2) = (30, 10), при котором целевая функция получает максимальное значение Fmax = F(x1, x2).
2.2. Аналитический метод решения задачи
Переходя от нестрогих неравенств к равенствам, то есть, переводя ограничения в разряд активных ограничений, получим систему уравнений с двумя неизвестными:
a11 x1 + a12 x2 ≤ b1
a21 x1 + a22 x2 ≤ b2
x1 ≥ 6
x2 ≥ 8
x1 ≥ 0
x2 ≥ 0
Например,
x1 + 5 x2 ≤ 80
3 x1 + 6 x2 ≤ 150
Систему двух уравнений с двумя неизвестными можно решить любым из известных способов (методом замены переменных, методом последовательного исключения переменных, т.е. методом Гаусса, методом Крамера и т.д.). Получим: x1 = 30, x2 = 10. Необходимо проверить и выполнение других ограничений: x1 ≥ 6, x2 ≥ 8, x1 ≥ 0, x2 ≥ 0 – полученное решение им удовлетворяет. Целевая функция при таких значениях аргументов будет иметь максимальное значение равное F(x1, x2) = 1.6 x1 + 6x2 = 1.6*30 + 6*10 = 108.
3. Выводы:
Для получения максимальной прибыли в заданных условиях (расход сырья, лимиты поставок, цены на ткань различного артикула) наиболее целесообразно выпустить и продать 300 тыс. м2 ткани первого артикула и 1000 тыс. м2 ткани второго артикула. Прибыль при этом составит 108 тыс. рублей.
 2017-12-14
2017-12-14 984
984







