Рівномірний закон розподілу

Тема: Основні закони розподілу неперервних випадкових величин.

Враховуючи, що між інтегральною та диференціальною функціями розподілу існує досить простий зв'язок (f(x)=F'(x) і 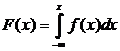), закон розподілу неперервної випадкової величини

можна задати, вказуючи лише щільність розподілу f(x).

Основними законами розподілу неперервних випадкових величин є рівномірний, показниковий і нормальний. Розглянемо їх детально.

Рівномірний закон розподілу.

Означення 1. Неперервна випадкова величина X називається

рівномірно розподіленою на відрізку [a,b], якщо щільність розподілу її стала на цьому відрізку і мас вигляд

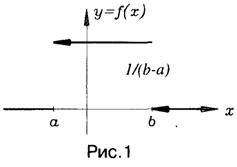
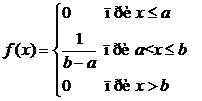(1)

Крива розподілу у = f(x) має вигляд (рис. 1):

Раніше ми знайшли функцію розподілу F(x):

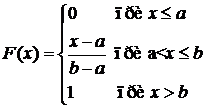(2)

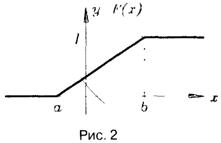
Її графік має вигляд (рис. 2):

Пркклад 1 Неперервна випадкова величина X розподілена

рівномірно па інтервалі (0,1). Знайти ймовірність попадання X (у результаті експерименту) в інтервал .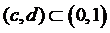

Розв'язання. Згідно з (1) знаходимо щільність розподілу X:

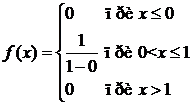
Тоді 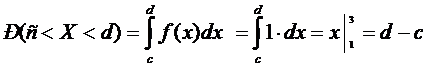, тобто

довжині відрізка [ c,d ].

Знайдемо числові характеристики рівномірно розподіленої неперервної величини.

Теорема 1. Якщо неперервна випадкова величина X розподілена

рівномірно на відрізку [ а,b], то її числовими характеристиками с:

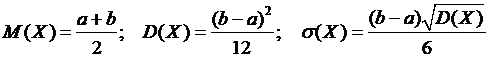. (3)

Доведення. Щільність розподілу рівномірно розподіленої величини X задана рівністю (1), тому знаходимо М(Х), D(X), 𝜎 (X).

Отже, математичне сподівання рівномірно розподіленої неперервної випадкової величини є середина відрізка.

2)

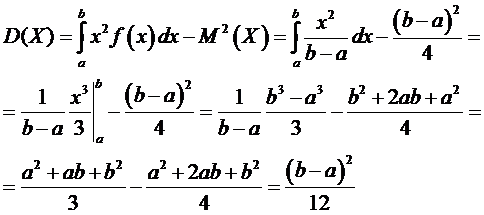
3)

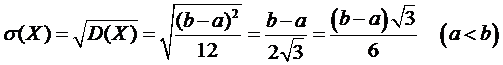
Теорему доведено.