Нормальний закон розподілу

Означення 3. Випадкова величина X називається розподіленою нормально з параметрами а, 𝜎, якщо щільність її ймовірності мас вигляд:

(7)

а її інтеграл

. (8)

називається нормальною функцією розподілу.

Нормальний закон розподілу з параметрами а і σ позначають N(a, 𝜎 ).

Розкриємо зміст параметрів a і σ нормального розподілу.

Теорема 3. Якщо неперервна випадкова величина X розподілена нормально, то її математичне сподівання дорівнює параметру а, а середнє квадратичне відхилення дорівнює σ.

Доведення. Враховуючи щільність розподілу (7), знайдемо числові характеристики.

1)
При доведенні ми використали рівності:

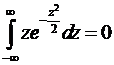(від непарної функції);

(інтеграл Пуассона).

2)

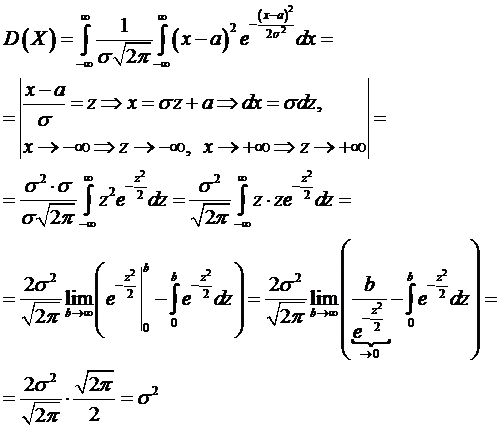
' Отже, D(X) = 𝜎 ² тому

3) .

Теорема доведена.

Зауваження 4. Функція щільності ймовірностей

називається ще функцією Гаусса, а розподіл, заданий нею - гауссівським розподілом.

Означення 4. Графік нормального розподілу називається нормальною кривою або кривою Гаусса.

Повне дослідження функції щільності ймовірностей f(x) методами диференціального числення дає її графік, зображений на рис. 5.

Тут вісь Ох (у = 0) є горизонтальною асимптотою, а пряма X — а - вісь симетрії. Досліджуючи f(x), знаходимо максимум функції

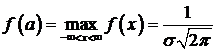, тому точка х — а є модою випадкової

величини (за означенням).

Властивості функції дозволяють дослідити вплив параметрів нормального розподілу на форму кривої Гаусса.

Так, зміна параметра а (математичного сподівання) не змінює форми кривої, а лише зсуває її вздовж осі Ох вправо або вліво в залежності від значення параметра а (рис. 6). Зміна ж параметра σ змінює форму кривої Гаусса. Якщо σ збільшується, то

f_max = f(a) зменшується, тобто крива стискується. Якщо ж aaa О спадає, то крива Гаусса розтягується у додатному напрямі осі Оу. Отже, зі збільшенням дисперсії σ² ймовірності значень, віддалених від центра розподілу, зменшуються (рис. 6).

Зауваження 5. Якщо випадкова величина X розподілена за нормальним законом з параметрами a = 0 і σ = 1, тобто N(0,l), то такий розподіл називається нормованим нормальним або стандартним роз­поділом. Функцією щільності у цьому випадку буде функція Гаусса

, графік якої симетричний відносно осі Оу, а інтеграл – функція Лапласа

(9)

Нагадаємо, що даний інтеграл не виражається в елементарних функціях, тому значення функції Лапласа знаходяться з таблиць.

Встановимо зв'язок між функцією розподілу F(x) і функцією Лапласа Ф(x). Згідно з рівністю (8) запишемо:

Отже, 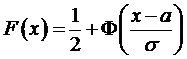(10)

де - функціяЛапласа.

Графіки цих функцій зображені на рис. 7 і рис. 8.

 

(, a - математичне сподівання X, σ - середнє квадратичне відхилення X).

Означення 5. Число М _e називається медіаною, якщо виконується

рівність

Якщо X розподілена нормально, то медіана М_е дорівнює а.

11.4. Ймовірність попадання випадкової величини X в інтервал (α,β). Правило трьох сигм.

Використовуючи формулу Р(α < X < β) = F(β) - F(α), а також рівність (9), одержимо формулу ймовірності того, що нормально розподілена випадкова величина X належатиме інтервалу (α,β)

(11)

Приклад 5. Випадкова величина X розподілена за нормальним законом. Математичне сподівання дорівнює 30, а середнє квадратичне

відхилення дорівнює 10. Знайти ймовірність того, що X набуде значення з інтервалу (10;50).

Розв'язання. Згідно з формулою (11) і за умови а = 30, σ = 10, обчислюємо шукану ймовірність

При розв'язуванні використали властивість непарності функції Лапласа

Ф (х) та її значення з таблиці: Ф(2) = 0,4772.

Приклад 6. Автомат випускає цукерки. Контролюється довжина

цукерки, що розподілена нормально. Математичне сподівання М(X) (тобто проектна довжина цукерки) дорівнює 50 мм. Фактична ж довжина цукерок коливається між 32 мм та 68 мм. Навмання вибирається одна цукерка. Яка ймовірність того, що вона буде довша за 55 мм?

Розв'язання. 1) Спочатку знайдемо середньоквадратичне відхи­лення

σ (X) = σ. За умовою задачі Р(32 < X < 68) = 1. Крім того відомо, що М(Х) = а = 50. Отже, маємо рівняння

або

Звідси знаходимо .За властивостями функції Лапласа можна покласти . Отже, .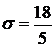
2) Далі обчислюємо шукану ймовірність

Значення функції Лапласа Ф(1,39)знаходимо з таблиць.

Обчислимо ймовірність відхилення випадкової величини X від її математичного сподівання. Згідно з рівністю (11) і непарністю функції Лапласа Ф(x), знаходимо:

Лапласа Ф(х), знаходимо:

Покладемо ε = 3σ. Тоді

Отже:

Якщо випадкова величина Xмає нормальний розподіл, то ймовірність її відхилення від математичного сподівання, яке більше трьох середньоквадратичних відхилень, близька до нуля.

З цього випливає " Правило 3σ ". З ймовірністю, близької до одиниці, значення нормально діленої випадкової величини лежать в інтервалі довжиною 6σ і центром а (рис. 9).

Зокрема, якщо неперервна випадкова величина розподілена за

стандартним законом N(0,l), то рівність (13) можна записати так:

(14)

Отримане правило означає що результатами вимірювань з відхиленнями від математичного сподівання більше, ніж на три сигми, нехтуємо як грубими помилкам_{и Така} процедура дає змогу істотно підвищувати надійність емпіричних даних.

На практиці це правило використовують ще й так: якщо закон розподілу випадкової величини X невідомий, але | X – а| < 3σ, то можна припустити, що X розподілена нормально

Приклад 7. Випадкова величина Xрозподілена нормально. Математичне сподівання і середнє квадратичне відхилення X відповідно дорівнюють 20 і 10. Знайти ймовірність того, що відхилення за абсолютною величиною менше трьох.

Розв'язання. Згідно з рівністю (12) і за умови ε = 3, а= 20, з таблиць значення Ф(0,3) = 0,1179. Отже, шукана ймовірність P(|X- 20|<3)=0,2358.

Запитання для самоконтролю.

1)Що таке рівномірний закон розподілу НВВ? Який вигляд мають функції щільності та а розподілу? Які їх графіки?

2)Обчисліть числові характеристики рівномірно розподіленої НВВ.

3)Що таке показниковий закон розподілу НВВ з параметром λ? Який вигляд мають функції щільності та розподілу?

4)Обчисліть числові характеристики НВВ, розподіленої за показниковим законом. Який вигляд має функція надійності?

5)Що називається нормальним законом розподілу НВВ з параметрами а, σ?

6)Обчисліть числові характеристики нормально розподіленої НВВ.

7)Який вигляд має графік нормального розподілу? Наведіть основні властивості нормальної кривої.

8)Сформулюйте правило трьох сигм. Де його використовують на практиці?