Типовые задачи с решениями. Типовые задачи с решениями и для самостоятельного решения

Типовые задачи с решениями и для самостоятельного решения

Задача 1. Пусть даны жестко закрепленные электрические заряды q₁, q₂, q₄ (рис. 1). Считая известными их величины и расстояние между ними, найти силу, действующую со стороны этих зарядов на пробный заряд q_пр, помещенный в свободную вершину квадрата.

Рис. 1

Так же как и в механике, в электростатике справедлив принцип независимости действия сил: каждая сила действует на тело так, как будто других сил, действующих на тело, нет. Выражение каждой из сил определяется законом Кулона

где диэлектрическая проницаемость (по умолчанию считаем, что заряды находятся в вакууме или в воздухе).

Используя принцип суперпозиции (наложения) сил, можно определить в данный момент времени результирующую силу, действующую на любой из зарядов со стороны других зарядов в случае схемы расположения зарядов на рис. 1 по правилам сложения векторов

или с учетом формулы закона Кулона

Ответ:

Задача 2. Два одинаковых металлических шарика заряжены одноименно так, что величина заряда на одном шарике в 5 раз больше, чем на другом. Шарики привели в соприкосновение и раздвинули на прежнее расстояние. Во сколько раз изменилась сила взаимодействия между шарами?

Дано: r₁=r₂

Решение

Будем считать, что оба шарика заряжены положительно. Для определения силы взаимодействия в обоих случаях воспользуемся законом Кулона: и (1), где и - заряды шариков после того, каких привели в соприкосновение и раздвинули на прежнее расстояние. Так как шарики одинаковые, то = . По закону сохранения электрического заряда можно записать q₁+q₂= + или 5q₂+q₂=2 откуда =3q₂ (2). С учетом (1) и (2) найдем отношение или .

Ответ: (сила взаимодействия увеличилась в 1,8 раза).

Задача 3. Два небольших одинаковых шарика с массами по 0,1 г подвешены в одной точке на нитях длиной 25 см. После того, как шарикам сообщили одинаковые заряды, они разошлись на расстояние 5 см. Определить заряды шариков. Шарики находятся в вакууме (ε= 1).

Дано: m₁=m₂=m=0,1г l=25 см ε=1 q₁=q₂=q r=5 см	СИ 10^{-4 кг} 25^.10^{-2 м} 5^.10^{-2 м}
q-?

Решение

Рассмотрим один из шариков. На него действуют три силы: - сила тяжести, - сила кулоновского взаимодействия с другим заряженным шариком, - сила натяжения нити. Запишем условие равновесия шарика в векторной форме: (1). В проекциях на оси выбранной системы координат уравнение (1) примет вид

для Ox: F_k+F_нsinα=0,

для Оу: F_н^.cosα-mg=0 (2).

Рис. 2

Исключив F_н из системы (2) и учитывая, что , получим . Поскольку угол α мал, то . Тогда , откуда (3). Подставив в (3) численные значения в системе СИ, находим Ответ: q=5,27^.10^-9 Кл.

Задача 4. Два одинаковых маленьких шарика подвесили на нитях равной длины, закрепленных в одной точке. Шарикам сообщили одинаковые по величине и знаку заряды. После этого шарики погрузили в жидкий диэлектрик, плотность которого r₁. Плотность шариков р. Найти диэлектрическую проницаемость среды, если угол расхождения нитей в воздухе равен a, а в жидкости b.

Рис. 3

Решение. До погружения в жидкость на каждый шарик действовали сила тяжести , сила натяжения нити , и сила отталкивания (см. рис. 3, а). Поскольку шарик находился в равновесии, то из равенства нулю суммы проекций на оси 0Х и 0Y сил, действующих на шарик, получим:

, .

Сила кулоновского отталкивания равна , где l – длина нити

Отсюда, разделив почленно первое уравнение на второе, с учетом выражения для , получим

. (1)

Когда шарики погружены в жидкость (см. рис. 3, б), на каждый из них действуют следующие силы: сила тяжести , сила натяжения нити , архимедова сила и сила отталкивания , модуль которой равен:

где e – диэлектрическая проницаемость жидкости.

Из условия равновесия шарика получим:

, .

Поскольку сила Архимеда равна , по аналогии получаем, что

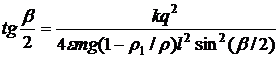. (2)

Разделив почленно равенство (1) на равенство (2), получим после преобразований

Ответ: .

Задача 5. Электрон влетает в плоский горизонтальный конденсатор параллельно его пластинам со скоростью v₀=10 Мм/с. Напряженность поля в конденсаторе Е=10 кВ/м, длина конденсатора l =5 см. Найти модуль и направление скорости электрона в момент вылета его из конденсатора. Насколько отклонится электрон от первоначального направления?

Рис. 4

Решение. Совместим начало координат с точкой, в которой находился электрон в момент влета в конденсатор, ось 0Х направим горизонтально, ось 0Y – вертикально вниз (рис. 4). В этой системе координат движение электрона можно представить как результат сложения двух прямолинейных движений: равномерного движения со скоростью v_x=v₀ в горизонтальном направлении и равноускоренного движения с некоторым ускорением вдоль оси 0Y. Наличие ускорения вдоль оси 0Y объясняется тем, что на электрон в этом направлении действует электрическая сила , е – заряд электрона. (Силой тяжести, действующей на электрон, пренебрегаем по сравнению с силой .)

Проекцию ускорения на ось 0Y найдем по второму закону Ньютона:

Выпишем начальные условия: х₀=0, у₀=0, v₀_X=v₀; v_Y=0. Тогда уравнения, определяющие зависимость координат х, у и проекций скорости от времени, будут иметь вид:

, , (1)