Векторные и матричные операторы

ЗАДАНИЕ НА ЛАБОРАТОРНУЮ РАБОТУ № 2

«ВЕКТОРА И МАТРИЦЫ»

1.

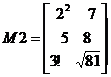
Упростить матрицы М1 и М2.

Составить новые матрицы М12 и М21, причем: М12 = М1 рядом с М2, М21 = М2 рядом с М1.

 

2. Заданы матрицы:

1) Найти матрицу W = 2V;

2) Найти сумму элементов V;

3) Найти определитель матрицы М;

4) Найти скалярное и векторное произведение V и W;

5) Найти матрицу, обратную М;

6) Найти транспонированную W;

7) Найти произведение прямой и обратной матриц М;

8) Решить систему уравнений MX=V; найти множество значений Х, сделать проверку.

 

3. Заданы матрицы:

Используя стандартные функции, найти:

1) Диагональную матрицу V;

2) Число строк и столбцов М;

3) Число элементов в V, индекс последнего элемента.

 

4.

При помощи функции submatrix извлечь элементы матрицы, расположенные между строками 1 и 2 и между столбцами 0 и 2 (включительно). При помощи этой же функции переставить в полученной матрице: а) столбцы; б) строки.

 

5.

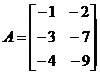
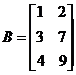
Объединить матрицы: 1) В под А; 2) А рядом с М.

 

ВЕКТОРНЫЕ И МАТРИЧНЫЕ ОПЕРАТОРЫ

Операция	Обозн.	Клав.	Описание
Умножение матрицы на скаляр	A∙z	*	Умножает каждый элемент А на скаляр z.
Скалярное произведение	u∙v	*	Возвращает скаляр: ∑ui∙vi. Векторы должны иметь одинаковое число элементов.
Матричное умножение	A∙B	*	Возвращает произведение матриц А и В, число столбцов А должно соответствовать числу строк в В.
Умножение матрицы на вектор	A∙v	*	Возвращает произведение матриц А и v, число столбцов А должно соответствовать числу строк v.
Деление		/	Делит каждый элемент массива на скаляр z.
Сложение векторов и матриц	A+B	+	Складывает соответствующие элементы А и В, массивы А и В должны иметь одинаковое число строк и столбцов.
Скалярная сумма	A+z	+	Добавляет z к каждому элементу А.
Векторное и матричное вычитание	A-B	-	Вычитает соответствующие элементы массива А из элементов массива В, массивы А и В должны иметь одинаковые размеры.
Скалярное вычитание	A-z	-	Вычитает z из каждого элемента А.
Изменение знака	-A	-	Умножает все элементы А на -1.
Степени матрицы, обращение матриц	Mn	^	n-ная степень квадратной матрицы М. n должно быть целым числом. М-1 представляет матрицу, обратную к М, другие отрицательные степени – степени обратной матрицы.
Длина вектора		|	Возвращает , где 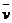- вектор, комплексо сопряженный к v.
Детерминант		|	Возвращает детерминант квадратной матрицы М. Результат – скаляр.
Транспонирование	AT	Ctrl+1	Возвращает матрицу, в которой строки – столбцы А, а столбцы – строки А. А может быть вектором или матрицей.
Векторное произведение		Ctrl+8	Возвращает векторное произведение для векторов с тремя элементами u и v.
Комплексное сопряжение		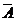“	Меняет знак мнимой части каждого элемента А.
Суммирование элементов	∑	Ctrl+4	Суммирует элементы вектора v. Возвращает скаляр.
Векторизация		Ctrl+-	Предписывает в выражении с А производить операции поэлементно.
Верхний индекс	A<n>	Ctrl+6	Извлекает n-ный столбец массива А. Возвращает вектор.
Нижний индекс вектора	vn	[	n-ный элемент вектора.
Нижние индексы матрицы	Am,n	[	Элемент матрицы, находящийся в m-ом ряду и n-ой строке.