Закон Ома для однородного участка цепи и закон Ома в дифференциальной форме

3.1. Ом в 1826 г. экспериментально установил закон, который называется законом Ома для однородного участка цепи:

ТОК, ТЕКУЩИЙ ПО ОДНОРОДНОМУ МЕТАЛЛИЧЕСКОМУ ПРОВОДНИКУ, ПРОПОРЦИОНАЛЕН ПАДЕНИЮ НАПРЯЖЕНИЯ U НА ПРОВОДНИКЕ", т. е.

I = (), (14)

где R - сопротивление проводника, измеряется в СИ в омах (Ом); из (14) следует, что 1Ом =1 В/1 А.

Сопротивление проводника R =ρl / S, (15)

где р - удельное сопротивление, измеряется в СИ вОм ×м.

Оно зависит от температуры: = T, где - удельное сопротивление при температуре t = 0°С, - температурный коэффициент сопротивления, близкий к 1/273 К , T- термодинамическая температура; так что с ростом температуры

сопротивление металлических проводников увеличивается. Качественная температурная зависимость удельного сопротивления металлического проводника представлена на рис.3

3.2. Закон Ома в дифференциальной форме

Найдем связь между векторами и . Для этого мыслен­но выделим в окрестности некоторой точки проводника элемен­тарный цилиндрический объем с образующими, параллельными векторам и , (см. рис. 4).

Между концами проводника длиной dl напряжение U = Edl, под действием которого через его поперечное сечение площадью dS течет ток I = jdS. Сопротивление цилиндрического проводника, в нашем случае, равно R = .Используя закон Ома для участка цепи I = , находим: jdS = , откуда и получаем закон Ома в дифференциальной форме = = , (16)

где = удельная электропроводность; [ ] = 1 / (Ом м) = 1 См / м, где 1 См = 1 / Ом – это единица измерения электропроводности в СИ, называемая сименс (См). Для металлов согласно классической теории электропроводности = , (17)

где n - концентрация свободных электронов, она может достигать 10 10 электрон / м ; e- заряд электрона, m - его масса; < > - средняя длина свободного пробега электрона; < v > = (18)

< v > - средняя скорость теплового движения электрона, k = 1,38 ×10 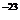Дж/К - постоянная Больцмана.

С учетом (18) из (17) следует, что ~ , а , тогда как опыт показывает, что ~ Т. Этот и другие недостатки классической теории электропроводности металлов устра­нила квантовая теория электропроводности.