Етап 1. Побудова простору допустимих рішень

1.1. Спочатку побудуємо вісі координат: на горизонтальній будуть вказуватись значення змінної х₁, а на вертикальній – х₂ (Рис. 3.1.)

1.2. Розглянемо умови невід*ємності змінних х₁ ≥ 0, х₂ ≥ 0. Це означає, що простір допустимих рішень буде знаходитись в правому верхньому квадранті.

1.3. Для врахування інших обмежень, проводимо на площині всі ці прямі.

6х₁ + 4х₂ ≤ 24 (1)

х₁ + 2х₂ ≤ 6 (2)

-х₁ + х₂ ≤ 1 (3)

х₂ ≤ 2 (4)

х₁ ≥ 0 (5)

х₂ ≥ 0 (6)

Щоб провести ці лінії, необхідно знайти дві різні точки, що лежать на цій прямій.

1.3.1

6х₁ + 4х₂ ≤ 24 (1)

якщо х₁ = 0, то х₂ =24/4 = 6; (0, 6)

якщо х₂ = 0, то х₁ =24/6 = 4 (4, 0)

Отже, наша пряма проходить через дві точки (0, 6) та (4, 0)

Лінія поділяє площину на дві полу-площини. Точки площини з однієї сторони задовольняють нерівності, а з іншої – ні. Тестовою точкою є точка (0, 0).

Підставляємо цю точку до першого рівняння:
6х₁ + 4х₂ ≤ 24 ®

6×0 + 4×0 = 0 ®

0 ≤ 24

Точка (0, 0) задовольняє рівнянню, тому допустимим полу-простором буде те, що містить цю точку. На рис. відмітимо цей простір стрілочкою з напрямом.

1.3.2

х₁ + 2х₂ ≤ 6 (2)

якщо х₁ = 0, то х₂ =6/2 = 3; (0, 3)

якщо х₂ = 0, то х₁ =6/1 = 6 (6, 0)

Отже, наша пряма проходить через дві точки (0, 3) та (6, 0)

Лінія поділяє площину на дві полу-площини. Точки площини з однієї сторони задовольняють нерівності, а з іншої – ні. Тестовою точкою є точка (0, 0).

Підставляємо цю точку до першого рівняння:
х₁ + 2х₂ ≤ 6 ®

0×0 + 2×0 = 0 ®

0 ≤ 6

Точка (0, 0) задовольняє рівнянню, тому допустимим полу-простором буде те, що містить цю точку. На рис. відмітимо цей простір стрілочкою з напрямом.

1.3.3

-х₁ + х₂ ≤ 1 (3)

якщо х₁ = 0, то х₂ =1/1 = 1; (0, 1)

якщо х₂ = 0, то х₁ =1/-1 = -1 (-1, 0)

Отже, наша пряма проходить через дві точки (0, 1) та (-1, 0)

Лінія поділяє площину на дві полу-площини. Точки площини з однієї сторони задовольняють нерівності, а з іншої – ні. Тестовою точкою є точка (0, 0).

Підставляємо цю точку до першого рівняння:
-х₁ + х₂ ≤ 1 ®

0×0 + 0×0 = 0 ®

0 ≤ 1

Точка (0, 0) задовольняє рівнянню, тому допустимим полу-простором буде те, що містить цю точку. На рис. відмітимо цей простір стрілочкою з напрямом.

1.3.4

х₂ ≤ 2 (4)

якщо х₁ = 0, то х₂ =2/1 = 2; (0, 2)

Отже, наша пряма є паралельною х₁ і проходить через точку (0, 2)

Лінія поділяє площину на дві полу-площини. Точки площини з однієї сторони задовольняють нерівності, а з іншої – ні. Тестовою точкою є точка (0, 0).

Підставляємо цю точку до першого рівняння:
х₂ ≤ 2 ®

0×0 = 0 ®

0 ≤ 2

Точка (0, 0) задовольняє рівнянню, тому допустимим полу-простором буде те, що містить цю точку. На рис. відмітимо цей простір стрілочкою з напрямом.

1.3.5

х₁ ≥ 0 (5)

х₂ ≥ 0 (6)

 

Це означає, що простір допустимих рішень буде знаходитись в правому верхньому квадранті. На рис. відмітимо цей простір стрілочкою з напрямом.

 

 

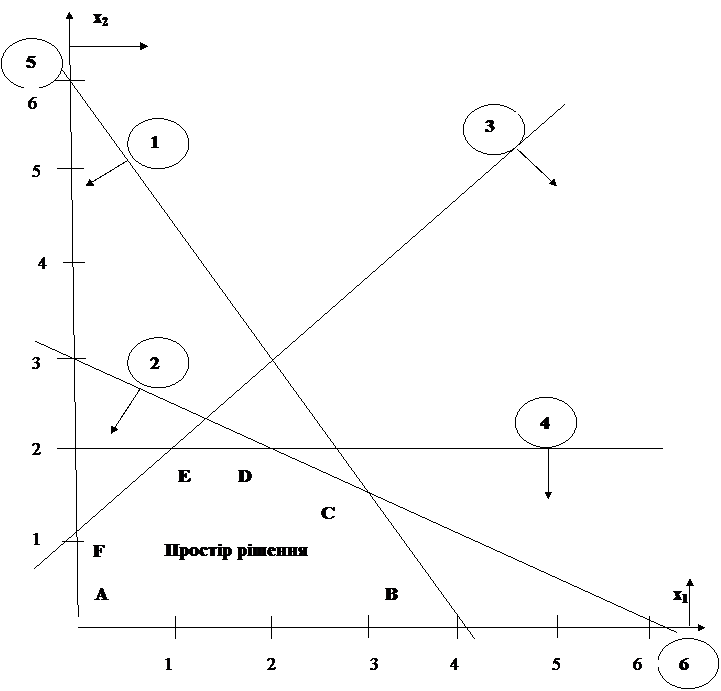
Рис. 3.1. Простір допустимих рішень моделі.

Етап 2. Пошук оптимального рішення.

2.1. Точки простору допустимого рішення на рис. 3.1. розположені всередині або на границі області, обмеженою ломаною кривою ABCDEF.
Так як простір допустимих рішень має нескінчену кількість точок, то необхідно знайти оптимальне рішення.

2.2. Необхідно знайти напрям збільшення цільової функції:
Максимізувати z = 5х₁ + 4х₂

Для цього прирівняємо z до декількох збільшуючихся значень. Наприклад 10 і 15.

Отримаємо такі рівняння прямих:

5х₁ + 4х₂ = 10

5х₁ + 4х₂ = 15

2.2.1.

5х₁ + 4х₂ = 10

якщо х₁ = 0, то х₂ =10/4 = 2,5; (0; 2,5)

якщо х₂ = 0, то х₁ =10/5 = 2 (2, 0)

Отже, наша пряма проходить через дві точки (0; 2,5) та (2, 0)

2.2.2.

5х₁ + 4х₂ = 15

якщо х₁ = 0, то х₂ =15/4 = 3,75; (0; 3,75)

якщо х₂ = 0, то х₁ =15/5 = 3 (3, 0)

Отже, наша пряма проходить через дві точки (0; 3,75) та (3, 0)

2.2.3. Ці прямі показано штрихованими лініями, а напрям зростання цільової функції – стрілкою.

 

2.3. Цільова функція може зростати до тих пір, поки не виходить за простір допустимих значень. Точка пересічення області допустимих значень і прямої, що дорівнює максимально можливому значенню цільової функції є точкою оптимуму.
на рис 3.2. видно, що оптимальним рішенням є точка С.

 

 

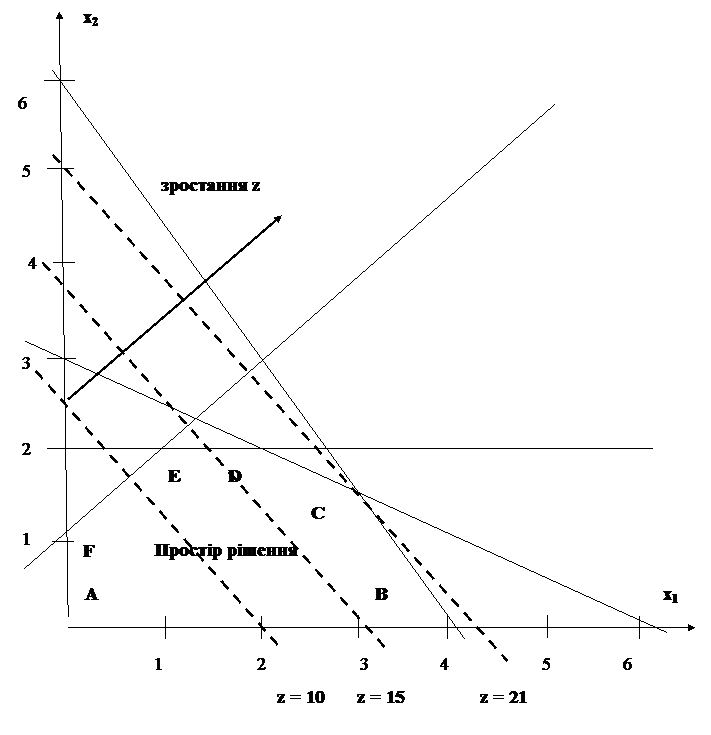
Рис. 3.2. Оптимальне рішення моделі.

2.4. Знайдемо координати точки С. Ця точка є місцем пересічення прямих (1) і (2), тому її координати знаходяться як рішення системи рівнянь, що задають ці прямі:

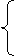6х₁ + 4х₂ = 24 (1)

х₁ + 2х₂ = 6 (2)

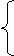6 ×(6 - 2х₂)+ 4х₂ = 24

х₁ = 6 - 2х₂

 

Рішення:

36 - 12 х2 + 4х2 = 24 - 8 х2= 24 – 36 8 х2= 12 х2= 12 / 8 х2= 1,5

х1 = 6 - 2х2 х1 = 6 - 2×1,5 х1 = 3

 

Отже, отримали координати точки С (3; 1,5).

2.5. При цьому значення цільової функції

Максимізувати z = 5х₁ + 4х₂

z = 5х₁ + 4х₂ = 5×3 + 4×1,5 = 15 + 6 = 21.

Це означає, що для компанії «СМАРТ» оптимальним вибором є щоденне виробництво 3 т фарби для зовнішніх робіт та 1,5 т – для внутрішніх робіт з щоденним доходом 21 тис.$.