Математичне сподівання ДВВ

Означення І. Математичний сподіванням ДВВ X називається число, яке дорівнює сумі добутків усіх її можливих значень на відповідні

ймовірності і позначається М(X):

(1)

Тут X - ДВВ, що набуває значення х_k з ймовірностями р_k, k = 1,n.

Зауваження 1. Якщо ДВВ X набуває зліченної множини можливих значень, то (2)

за умови, що даний ряд абсолютно збіжний.

Зауваження 2. З означення випливає, що М(X) не випадкова, а стала величина (на відміну від випадкової величини X).

Приклад 1. Знайти М\ X) випадкової величини X, яка означає кількість появи гербів при підкиданні трьох монет.

Розв'язання. За умовою випадкова величина X означає кількість

гербів. Наведемо таблицю усіх можливих значень, яких набуває X, та їх ймовірності.

Ω	ГГГ	ГГЦ	ГЦГ	ЦГГ	ГЦЦ	ЦГЦ	ЦЦГ	ЦЦЦ
X
Р

X
p

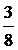
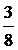
Тепер запишемо закон розподілу X:
Контроль:

Знайдемо М(Х) за формулою(1)

Зауваження З Математичне сподівання числа появи події А в одному випробуванні дорівнює ймовірності цієї події. Дійсно, M(X) = 0 ∙ q + 1∙p= p.

Зауваження 4. Математичне сподівання наближено дорівнює (тим точніше, чим більше число випробувань п) середньому арифметичному значень випадкової величини, що спостерігається. У цьому полягає

ймовірнісний зміст М (X).

Зауваження 5. Очевидно, М(Х) більше найменшого і менше

найбільшого з можливих значень ДВВ X:

min(x₁,х₂,...,х_n)< М(Х)<тaх(х₁,х₂,...,х_п).

Отже, М(Х) характеризує розміщення значень випадкової величини X.

Зауваження 6. (Механічний зміст формули (1)). Запишемо формулу (1) у вигляді

(3)

Нехай р_к - маси матеріальних точок, розміщених на числовій осі, а х_k - координати цих точок. Тоді формулу (3) можна розглядати як формулу центра ваги системи матеріальних точок (рис. 1).