2018-01-08
869
1. Передумови й особливості використання пакета
Нейромережевий Інструментарій Matlab (NNT Matlab) - універсальне нейронне мережне середовище. У пакет включено практично усе, що стосується процедур створення нейронних мереж і аналізу отриманих результатів, зокрема їхньої інтерпретації. Варто визнати, що документація, що поставляється з пакетом, не просто жахає користувача (навіть досвідченого) своїм розміром, але і своєї, скажімо так, своєрідністю, що дуже незвичайно сприймається читачем з технічною освітою, отриманою на Пост- Радянському просторі. Читача законно дивує те, що багаторазово повторюються досить прості речі, у той час як про принципові положення говориться абсолютно мимохідь. У даному виданні ми обмежуємося версією 3.0 NNT. Новітня версія - 4.0, доступна з Matlab 6.0 (R12), і існує на ринку України. Ціль - спробувати пояснити користувачу, що не має спеціальної математичної освіти, як вирішувати прикладні інженерні задачі, використовуючи можливості програми ToolBox Neural Net зі складу математичного пакета MatLab. З практичної точки зору визнано доцільним розглянути наступні питання:
|
|
|
1. Загальне введення в прикладні нейронные мережі.
· Шаруваті нейронные мережі:
· Конструювання шарів.
· З'єднання шарів.
· Установка функцій передачі.
· Ваги і зсуви.
· Функції тренувань і параметри
· Відмінності тренувань від адаптації
· Функції виконання
· Параметри тренувань
· Параметри адаптації
Нейронний Мережний Інструментарій системи математичного моделювання Matlab (NNT) могутнє, але все-таки ще іноді цілком незрозуміле знаряддя рішення цілого ряду задач, котрі відомими методами не вирішуються, чи їхні рішення зв'язані з великими технічними труднощями. Це пояснюєеться головним чином складністю створеного мережного об'єкта. Навіть якщо високорівнева мережна модель ефективно функціонує, подібно функціям newp і newff, що включаються в створений мережний об'єкт, ймовірно буде потрібно ще визначений час, щоб користувач міг самостійно редагувати свої власні об'єкти і правильно інтерпретувати результати.
У даному посібнику нейронні мережі розглядаються практично і прагматично. При цьому автори ставлять головною задачею на першому етапі навчання - бачення лісу за деревами: студенти й аспіранти (основний контингент, на який розрахована книга) і ін. користувачі повинні починати свої заняття з розуміння ідеології нейронних мереж, але не з програмування і реалізації отриманих програм, призначених для створення мереж. Створене програмне забезпечення повинне бути таким, щоб сховати багато деталей мережного об'єкта за ГРАФІЧНИМ ІНТЕРФЕЙСОМ КОРИСТУВАЧА Matlab. У ході запису такого програмного продукту, природно використовувати файл підказок (із усіма його недоліками), але більшість питань розв¢язується одним способом - методом спроб і помилок. Цьому сприяє і сама ідеологія нейронних мереж.
|
|
|
Математична нотація нейронних мереж, прямо зв'язана з об¢єктно-орієнтованим програмуванням, природно повинна розглядатися (хоча б у самому елементарному виді). Проте, можна думати, що вивчивши запропонований матеріал, користувач одержить досить пристойний об'ем знань, умінь і навичок, щоб будувати власні мережні моделі, достатні для рішення досить складних прикладних задач. Для більш складних задач необхідно ретельно вивчати специфічну Matlab-документацію, необхідну для врахування специфічних деталей і особливостей задачі.
Усі Matlab- команди, приведені в документації й у книзі приймають наявність NNT- мережного об'єкта, що називається "мережа"(net). Для того, щоб створити такий об¢єкт [1], необхідно набрати в командному рядку команду
>> net = net
яка дає "чисту" мережу, тобто без «особливостей» (характеристик), що визначають специфіку задачі. Які характеристики мережі необхідно установити і як установлювати їх - предмет цього практикума.
Мережні шари. У NNT поняття “шар” визначен як шар нейронів, за винятком вхідного шару. Так, у NNT - нотації (термінології) одношарова мережа має вид:
Рис.П2.1 Одношарова нейросеть (схема в нотації MatLab - Nnet)
У свою чергу тришарова мережа має вид - мал.П2.2:
Рис.П2.2. Тришарова нейронная мережа
Ми використовуємо останню мережу як приклад при викладі матеріалу. Кожен шар має багато специфічних особливостей (характеристик). Найбільш важливої тут є функції передачі нейрона в цьому шарі і функція, що визначає чистий внесок кожного нейрона, що має свою вагу, і вихід попереднього шару.
Створення шару. Порожній мережний об'єкт, що називають "мережа", буде створений у робочій області користувача, якщо набрати в командному рядку
>> net = net;
Визначимо особливості вхідного шару. Одношарова мережа встановлюється командою:
>> net.numInputs = 1;
Тепер ми повинні визначити кількість нейронів у вхідному шарі. Їхнє число повинне дорівнювати розмірності вхідних даних, визначених раніш - net.inputs{і}.size, де і - індекс (кількості) вхідних шарів. Так, щоб створити мережу, що має 2-вимірний вхід, необхідно набрати:
>> net.inputs{1}.size = 2;
Це визначає (зараз) вхідний шар.
Наступні характеристики - net.numLayers – встанолюютьзагальне число шарів у мережі, і net.layers{і}.size – визначають кількість нейронів у i-тім шарі. Щоб сформувати, наприклад, двошарову мережу, необхідно визначити 2 додаткових шари (схований шар з 3 нейронами і вихідний шар з 1 нейроном) шляхом використання групи команд:
>> net.numLayers = 2;
>> net.layers{1}.size = 3;
>> net.layers{2}.size = 1;
З'єднання шарів. Тепер необхідно визначити, які шари необхідно зв'язувати. Спочатку необхідно визначитися з яким шаром зв'язані входи. Встановлюють net.inputConnect(n) рівним 1 для відповідного шару і (звичайно перший), тому n = 1. З'єднання з іншою частиною шарів визначаються матрицею зв'язків, що називають net.layerConnect, що може мати значення елементних даних як 0 чи 1. Якщо елемент (і,j) = 1, значить вихід (outputs) шару j підключається до входу (inputs) шару і. Також необхідно визначити який шар є вихідним шаром, що виконується установкою net.outputConnect(і) у 1 для відповідного шару. Наприкінці необхідно визначити: які шари підключаються до цільових величин. (Звичайно, це буде вихідний шар). Таку задачу вирішують за допомогою установки net.targetConnect(і) у 1 для відповідного шару.
Так, для нашого приклада (двошарової мережі), відповідні команди повинні бути
>> net.inputConnect(1) = 1;
>> net.layerConnect(2, 1) = 1;
>> net.outputConnect(2) = 1;
|
|
|
>> net.targetConnect(2) = 1;
Установка Функцій Передачі. Кожен шар має власну функцію передачі, що встановлюється за допомогою команди net.layers{і}.transferFcn. Так, для того, щоб задати використання sigmoid функції передачі на першому шарі, і лінійну функцію передачі на другому шарі, використовують
>> net.layers{1}.transferFcn = ‘logsig’;
>> net.layers{2}.transferFcn = ‘purelin’;
Списки можливих функцій передачі знаходиться в Matlab-документації. Нижче (мал.П2.3) приведені піктограми деяких функцій передачі
Рис.П2.3. Піктограми функцій передачі
Ваги і зсуви. Для їхньої установки необхідн попередньо визначити, які шари повинні мати зсуви, встановити їх, виставляючи елементи net.biasConnect у 0 чи 1, де net.biasConnect(і) = 1 шар, що має засоби для установки зсувів.Щоб підключити зсуви в кожнім шарі в прикладі нашої мережі, ми повинні використовувати команду
>> net.biasConnect = [ 1; 1];
Тепер необхідно вирішити питання про процедуру ініціаліації ваг і зсувів. Якщо всі установки зроблені правильно, можна просто виконати команду
>> net = init(net);
Це дозволить відновити усі ваги і зсуви відповідно зробленому вибору. Перше, що необхідно зробити - втановитиnet.initFcn. Якщо немає необхідності формувати власну програму ініціалізації, команда 'initlay' дозволяє визначити шлях, яким варто йти, для рішення задачі. Це дозволяє ваги і зсуви кожного шару ініціалізувати, використовуючи свою власну програму ініціалізації.
>> net.initFcn = 'initlay';
Визначити точно, яка з функцій була використана, можливо через команду net.layers{і}.initFcn для кожного шару. Практично використовують два типи опцій:опції ініціалізації Nguyen-Widrow (типу 'підказки initnw' щодо деталей) і 'initwb', що дозволяє вибирати ініціалізацію для кожного комплекту ваг і зсувів окремо. Для використання 'initnw необхідно установити
>> net.layers{і}.initFcn = 'initnw';
для кожного шару ініціалізація буде виконана.
При використанні 'initwb' користувач повинний визначити програму initalization для кожного комплекту ваг і зсувів окремо. Найбільш загальна опція тут - RAND, що встановлює ваги як довільні (випадкові) числа між -1 і 1. Спочатку використовують команду
|
|
|
>> net.layers{і}.initFcn = 'initwb' '
для кожного шару. Потім визначають initalization для вхідної ваги,
>> net.inputWeights{1,1}.initFcn = 'rand';
і для кожного комплекту зсувів
>> net.biases{³}.initFcn = 'rand';
è çàãðóæàþò ìàòðèöû âåñîâ
>> net.layerWeights{i, j}.initFcn = ‘rand’;
де net.layerWeights{i,j} позначає вага від шару j до шару і.
Тренувальні функції і параметри, розбіжність між тренуванням і адаптацією (пристосуванням).
Один з найбільше інтуїтивно несприйманих аспектів NNT - розбіжність між тренуванням (train) і адаптацією (пристосуванням) (adapt). Як функції (тренувань), так і параметри (пристосовування) можуть одночасно чи по черзі використовуватися для підготовки однієї і тієї ж нейронної мережі. Розглянемо, у чому складається розбіжність між ними. Найбільше важливо те, що одне поняття повинне виконуватися пошагово (відновлення ваг після представлення кожного окремого зразка підготовки) проти пакета, коли відновлення ваг відбувається після кожного представлення всієї множини даних. При використанні пристосовування, як покрокова так і пакетна підготовка можуть бути застосовані. Використання кожного засобу окремо залежить від формату підготовки тренувальної множини. Якщо воно складається з двох матриць вхідних і цільових векторів, подібно робити так, як приведено нижче
>> P = [ 0.3 0.2 0.54 0.6; 1.2 2.0 1.4 1.5]
P =
0.3000 0.2000 0.5400 0.6000
1.2000 2.0000 1.4000 1.5000
>> T = [ 0 1 1 0 ]
T =0 1 1 0
мережа буде скоригована на використання пакетної підготовки. (У цьому випадку, у нас є 4 зразки: два 2 -мірних вхідних вектори, і 4 відповідних одномірних цільових вектори). Якщо підготовка установки дається у формі масиву осередків,
>> P = {[0.3; 1.2] [0.2; 2.0] [0.54; 1.4] [0.6; 1.5]}
P =[2x1 double] [2x1 double] [2x1 double] [2x1 double]
>> T = { [0] [1] [1] [0] }
T =[0] [1] [1] [0]
те це приведе до використання покрокової підготовки
Використовуючи, з іншого боку, тренування, необхідно згрупувати множини тренувальних даних незалежно від формату даних (Можливе використання обох методів). Великий плюс тренувань полягає в тому, що це дає великий вибір тренувальних функцій (градієнтний спуск, алгоритми Levenberg-Marquardt, і т.п.), що реалізовані досить ефективно. Так, якщо не існує достатніх основ для покрокової підготовки, тренування - ймовірно найкращий вибір. (При цьому звичайно зберігаються встановлені параметри).
Для того, щоб завершити цей розділ, необхідно відзначити, що ця розбіжність формальна складається як розбіжність між проходами й епохами. Якщо використовують пристосовування, працює характеристика, що визначає скільки разів повний набір даних тренувань використовуються для підготовки мережі, на net.adaptParam.passes. При використанні тренувань, ця ж характеристика тепер названа net.trainParam.epochs! (На нашу думку, це розбіжності абсолютно суб'єктивні по своїй природі і викликані, очевидно тим, що ці частини алгоритму готували різні люди).
Функції Виконання. Дві найбільш загальні опції, що використовуються тут, це Середня Абсолютно Помилка (mae) і Середньо-Квадратична Помилка (mse). Середня Абсолютна Помилка (mae) звичайно використовується в мережах для класифікації, у той час як Середньо-квадратична помилка(mse) найбільше часто використовується у функціо-нальних мережах апроксимации. Функція виконання встановлюється командою net.performFcn опцією, наприклад:
>> net.performFcn = 'mse';
Параметри тренувань. Якщо користувач збирається готувати власну мережу, використовуючи train, останній крок визначається командою net.trainFcn, і встановлює відповідні параметри за допомогою net.trainParam. Які параметри представити залежить від вибору тренувальних функцій.Так, якщо тренувати мережа, використовуючи градієнтний спуск, необхідно встановлювати
>> net.trainFcn = 'traingdm ';
і потім установити параметри
>> net.trainParam.lr = 0.1;
>> net.trainParam.mc = 0.9;
у бажаних межах. (У цьому випадку, lr - рівень навчання, і mc - термін рушійної сили.). Для конкретних задач необхідний перегляд Маtlаb-документації для визначення можливих функцій поготовки та вибору їхніх параметрів. Два інших корисних параметри - net.trainParam.epochs, що являє собою максимальну кількість випадків,коли повний набір даних може використовуватися для тренувань, і net.trainParam.show, що визначає час між повідомленнями статусу підготовки функції.
Наприклад,
>> net.trainParam.epochs = 1000;
>> net.trainParam.show = 100;
Параметри адаптації (adapt). Аналогічна загальна схема також використовується в установці параметрів пристосовування. Спочатку необхідно установити команду net.adaptFcn з бажаною функцією адаптації. Ми використовуємо adaptwb (пристосовувати вагу і зсуви), що бере до уваги окремі алгоритми корекції для кожного шару.
>> net.adaptFcn = 'adaptwb ';
Потім, оскільки ми використовуємо adaptwb, необхідно установити функції для навчання усіх ваг і зсувів:
>> net.inputWeights{1,1}.learnFcn = 'learnp';
>> net.biases{1}.learnFcn = 'learnp';
У цьому прикладі ми використовували learnp (Персептронне правило навчання). Наберіть у командному рядку 'help learnp' і прочитайте усе,що стосується персептрона). Корисний параметр - net.adaptParam.passes, що визначає максимальну кількість разів використання повного набору тренувальних даних для відновлення мережі:
>> net.adaptParam.passes = 10;
1.1 Основи практичного використання MATLAB & Neural Network Toolbox & Simulink (приклади побудови нейронних мереж і програм у нейромережевому логічному базисі для рішення прикладних задач)
Побудова будь-який нейронной мережі складається з 3-х головних етапів, показаних на блок-діаграмі
| Створення об'єкта нейронна мережа і його ініціалізація (Використовується команда newff) | |
| Тренування нейронної мережі (Використовується команда train -пакет тренувань) | |
| Порівняння результату комп¢ютерного виходу нейронної мережі з тренувальними даними й оцінюваними величинами (Використовується команда sim) |
Команда newff визначає нейромережу (тип архітектури, розмір і тип алгоритму тренування, що буде використовуватися. При цьому також автоматично ініціалізується НМе. Останні дві букви команди newff указують на тип НМе - f eed f orward network. Для радіальних базових функцій використовують НМе newrb і для самоорганізованих карт Кохонена використовують НМе (SOM) newsom.
З методичної точки зору доцільно досконально вивчити демонстраційну версію пакета MATLAB - NeuralNetwork Toolbox demos. Потрібно в командному рядку набрати demo і демонстраційне вікно MATLAB Demos window відкриється. Потрібно обрати Neural Networks у вікні Toolboxes і потім вивчати різні вікна. На мал.П2.4 приведене демонстраційне вікно
Рис.П2.5. Демонстраційне вікно MatLab
Задача 1: Обчислити функцію humps з пакета MATLAB. Задано y = 1./ ((x-.3).2 +.01) + 1./ ((x-.9).2 +.04) - 6; у MATLAB можемо зробити виклик функції через humps. Розглянемо можливість відтворення цієї функції через дані, сгенеровані НМе в інтервалі [0,2] за допомогою humps-функції:
a) використовувати багатошаровий персептрон на даних з різними розмірами нейронних мереж і різними навчальними алгоритмами;
b) повторити рішення задачі на мережі з РБФ.
Рішення:
Сформуємо дані, використовуючи команди
x = 0:.05:2; y=humps(x);
P=x; T=y;
Графічне представлення даних
plot(P,T,’x’)
grid; xlabel(’time (s)’); ylabel(’output’); title(’humps function’)
Рис.П2.6. Графічне представлення функції
y = 1./ ((x-.3).2 +.01) + 1./ ((x-.9).2 +.04) - 6
Навчальний алгоритм для багатошарової персептронної нейромережі має таку структуру:
a. Ініціалізація параметрів НМе, ваг і зсувів перед початком використання инициализирующих процедур. У цей же самий час відбувається визначення структури НМе.
b. Визначення параметрів, зв'язаних з алгоритмом, зокрема, помилка мети, максимальна кількість епох (ітерацій) і т.д.
c. Виклик навчального алгоритму.
% DESIGN THE NETWORK
% ==================
%First try a simple one – feedforward (multilayer perceptron) network
net=newff([0 2], [5,1], {'tansig','purelin'},'traingd');
% Here newff defines feedforward network architecture.
% The first argument [0 2] defines the range of the input and initializes the network parameters.
% The second argument the structure of the network. There are two layers.
% is the number of the nodes in the first hidden layer,
% 1 is the number of nodes in the output layer,
% Next the activation functions in the layers are defined.
% In the first hidden layer there are 5 tansig functions.
% In the output layer there is 1 linear function.
% ‘learngd’ defines the basic learning scheme – gradient method
% Define learning parameters
net.trainParam.show = 50; % The result is shown at every 50 th iteration (epoch)
net.trainParam.lr = 0.05; % Learning rate used in some gradient schemes
net.trainParam.epochs =1000; % Max number of iterations
net.trainParam.goal = 1e-3; % Error tolerance; stopping criterion
%Train network
net1 = train(net, P, T); % Iterates gradient type of loop
% Resulting network is strored in net1
TRAINGD, Epoch 0/1000, MSE 765.048/0.001, Gradient 69.9945/1e-010
….
TRAINGD, Epoch 1000/1000, MSE 28.8037/0.001, Gradient 33.0933/1e-010
TRAINGD, Maximum epoch reached, performance goal was not met.
Ціль досягається після 1000 ітерацій (епох).
ЗАУВАЖЕННЯ 1: Якщо при виконанні задачі спостерігати точно такі ж чи числа, таке ж саме виконання не вдається, це не повиннео дивувати. Це зумовлено тим, що newff використовує генератор випадкових чисел при створенні початкових значень ваг НМе. Таким чином,початкова НМе буде різною, навіть при використанні абсолютно тих самих команд.
Збіжність ітераційного процесу приведена на мал.П2.7.
Рис.П2.7. Збіжність ітераційного процесу рішення задачі.
З мал.П2.7 видно, що навіть збільшення кількості ітерацій не приводить до підвищення точності. Проконтролювати, як НМе виконує процедуру апроксимації можна в такий спосіб:
% Simulate how good a result is achieved: Input is the same input vector P.
% Output is the output of the neural network, which should be compared with output data
a= sim(net1,P);
% Plot result and compare
plot(P,a-T, P,T); grid;
Рис.П2.8. Вид кривої, відтвореної НМе
Пристосовність, як видно, є поганою, особливо на початку. Причина? Дві речі присутні тут. В усіх НМе ми маємо проблеми з визначенням крапки оптимуму і розміру мережі. Якщо робити розмір мережі великим, то потрібно збільшувати кількість мережних параметрів. Друга річ, яку можна виконати - це підвищити рівень виконання алгоритму чи навіть змінити алгоритм. Пізніше повернемося до розгляду цього питання.
Збільшення розміру НМе, використовується 20 вузлів на схованому шарі.
net=newff([0 2], [20,1], {’tansig’,’purelin’},’traingd’);
%Надаємо мережі нові алгоритмічні параметри і начи-%наймання тренувальний процес
net.trainParam.show = 50; % The result is shown at every 50 th iteration (epoch)
net.trainParam.lr = 0.05; % Learning rate used in some gradient schemes
net.trainParam.epochs =1000; % Max number of iterations
net.trainParam.goal = 1e-3; % Error tolerance; stopping criterion
%Train network
net1 = train(net, P, T); % Iterates gradient type of loop
TRAINGD, Epoch 1000/1000, MSE 0.299398/0.001, Gradient 0.0927619/1e-010
TRAINGD, Maximum epoch reached, performance goal was not met.
Кінцева помилка 0.001 не досягнута, але ситуація істотно покращилася. З кривої збіжності можна зробити висновок, що якщо поліпшити мережні параметри, зокрема кіль-кість ітерацій (епох), то можна збільшити шанси рішення задачі. Оскільки відомо, що градієнт, обчислений по методу backpropagation є повільним, треба спробувати застосувати більш ефективний алгоритм підготовки.
Використання алгоритму Levenberg-Marquardt – trainlm. Використовуємо менший розмір мережі– 10 вузлів на першому схованому слойе.
net=newff([0 2], [10,1], {’tansig’,’purelin’},’trainlm’);
%Define parameters
net.trainParam.show = 50;
net.trainParam.lr = 0.05;
net.trainParam.epochs =1000;
net.trainParam.goal = 1e-3;
%Train network
net1 = train(net, P, T);
TRAINLM, Epoch 0/1000, MSE 830.784/0.001, Gradient 1978.34/1e-010
….
TRAINLM, Epoch 497/1000, MSE 0.000991445/0.001, Gradient 1.44764/1e-010
TRAINLM, Performance goal met.
Збіжність показана на мал.П2.9.
Рис.П2.9. Збіжність процесу навчання
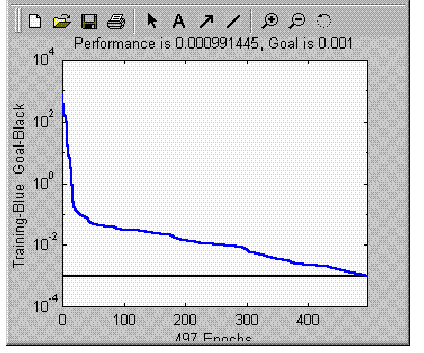
Рис.П2.9-1. Збіжність для нових параметрів моделі
Виконання тепер відповідає специфікациям
%Simulate result
a= sim(net1,P);
%Plot the result and the error
plot(P,a-T,P,T)
xlabel('Time (s)'); ylabel('Output of network and error'); title('Humps function')
Рис.П2.10. Відтворення кривої по методу Levenberg- Marquardt
З малюнка видно, що L-M алгоритм значно більш швидкий і має визначені переваги над методом зворотного поширення. Треба мати на увазі, що в залежності від ініціалізації алгоритм сходиться повільно чи більш швидко. Якщо питання про пристосування не знімається, то потрібно враховувати недолік даних і загамованість даних. Якщо функція є недостатньо гладкою, багатошаровий персептрон може мати проблеми. У цьому випадку треба повторити моделювання з незалежними даними.
x1=0:0.01:2; P1=x1;y1=humps(x1); T1=y1;
a1= sim(net1,P1);
plot(P1,a-a1,P1,T1,P,T)
Похибка представлення можемо бачити на мал.П2.11, що приведено нижче. Такі дані називають даними тесту. Інше спостереження може бути таким, що для випадку недостатньо гладких кривих, НМе може мати великі труднощі
Нейромережі з радіальними базисними функціями. У цьому прикладі спробуємо знайти функцію, яка б найбільше підходила б до заданих 41 крапці даних, використовуючи радіальну базисну мережу (РБМ). РБМ - мережа з двома шарами, вона складається зі схованого шару радіальних базисних нейронів і вихідного шару лінійних нейронів. Нижче приводиться типова форма радіальної базисної функції передачі, що використовується схованим шаром
p = -3:.1:3;
a = radbas(p);
plot(p,a)
Рис.П2.11. Радіальна базисна функція radbas(p)
Вага і зсув кожного нейрона в схованому шарі визначають позицію і ширину РБФ. Кожен лінійний вихідний нейрон формує зважену суму цих РБФ. Якщо ваги і величини зсувів для кожного шару обрані правильно і схований шар має достатню кількість нейронів, РБФ можна приспосувати для апроксимації будь-якої функції з будь-якою бажаною точністю. Можна використовувати функцію newrb, щоб швидко створити РБМ, що апроксимує функцію в цих крапках даних. Команди підказок MATLAB дають такий опис алгоритму.
Спочатку RADBAS шар не має нейронів. Наступні кроки повторюються, поки мережний засіб не вирівняє похибка нижче зазначеної МЕТИ.
1) Мережа симулюється
2) Знаходиться вхідний вектор з найбільшою похибкою.
3) Окремий RADBAS - нейрон додається з вагами рівними цьому вектору.
4) Ваги на PURELIN шарі модифікуються, щоб зменшити похибку.
Генерація даних виконується як у попередніх прикладах
x = 0:.05:2; y=humps(x);
P=x; T=y;
Використовуємо найпростішу форму команди newrb
net1 = newrb(P,T);
Для humps нейромережі тренування приводить до сингулярності, у такий спосіб тренування утруднюється. Симулюємо мережу і відтворюємо результат (мал.П2.12)
a= sim(net1,P);
plot(P,T-a,P,T)
Рис.П2.12. Результат апроксимації з використанням РБФ
Графік показує, що мережа апроксимувала максимуми з досить невеликими похибками. Проблема полягає в тому, що вбудовані величини двох параметрів мережі недостатньо гарні. За замовчуванням величина мети - середньо-квадратична похибка мети = 0.0, розширення - РБФ = 1.0. У нашому прикладі перший параметр = 0.02, другий = 0.1.
goal=0.02; spread= 0.1;
net1 = newrb(P,T,goal,spread);
Симулюємо і відтворюємо результат
a= sim(net1,P);
plot(P,T-a,P,T)
xlabel(’Time (s)’); ylabel(’Output of network and error’);
title(’Humps function approximation - radial basis function’)
Рис.П2.13. Відтворений результат
Цей вибір приводить до досить різних кінцевих результатів, як це видно з графіка. Виникає питання, яким повинне бути значення невеликої величини поширення. Як розу-міти - великий? Проблема в першому випадку була в тім, що була надзвичайно великою величина поширення (невиконання = 1.0), що приводить до досить рідкого рішення. Вивчення алгоритму вимагає матричної інверсії і як наслідок - виникають проблеми із сингулярностью. Більш раціональний вибір величини поширення дає кращий результат. [2]
ЗАДАЧА 2. Обчислити (відновити) поверхню, описанну як z = cos (x) sin (y) і визначену на квадраті -2 Ј хЈ 2, -2 Ј уЈ 2.
a) Графічно відтворюємо поверхню як функцію від x і y. Це демо-функция MATLAB, що ми також знаходимо в бібліотеці допомоги.
b) Сконструюємо НМе, що пристосує дані. Необхідно вивчити інші можливі альтернативи і протестувати кінцевий результат, пороінюючи похибку.
РІШЕННЯ
%Генерування даних
x = -2:0.25:2; y = -2:0.25:2;
z = cos(x)’*sin(y);
%Графічне відтворення поверхні (використовується сітка розміром 0.1)
mesh(x,y,z)
xlabel(’x axis’); ylabel(’y axis’); zlabel(’z axis’);
title(’surface z = cos(x)sin(y)’);
gi=input(’Strike any key...’);
pause
Рис.П2.14. Графічне відтвороення поверхні
Збережемо дані як вхідну матрицю P і вектор виходу T. Будемо використовувати порівняно невелику кількість нейронів на першому шарі, скажімо,25, і 17 на виході. Проініціллізуємо мережу
P = [x;y]; T = z;
net=newff([-2 2; -2 2], [25 17], {’tansig’ ’purelin’},’trainlm’);
%Застоуєм Levenberg-Marquardt алгоритм
%Define parameters
net.trainParam.show = 50;
net.trainParam.lr = 0.05;
net.trainParam.epochs = 300;
net.trainParam.goal = 1e-3;
%Train network
net1 = train(net, P, T);
gi=input(’Strike any key...’);
TRAINLM, Epoch 0/300, MSE 9.12393/0.001, Gradient 684.818/1e-010
TRAINLM, Epoch 3/300, MSE 0.000865271/0.001, Gradient 5.47551/1e-010
TRAINLM, Performance goal met.
Графічно відтворимо розвиток похибки
Рис.П2.15. Розвиток (зміна похибки)
Симулюємо відповідь НМе і графічно відтвороюємо поверхнюь (рис.П2.16)
mesh(x,y,a)
Рис.П2.16 Результат воспроизведения поверхности НМе
Результат має жосить перконливий вигляд, обстеження свідчить, що у певних областях апроксимація недосить висока.
Відмітимо рис.2.16 може здаватися кращим для аналізу, ніж зображення поверхні похибки (рис.2.17)
% Error surface
mesh(x,y, a-z)
xlabel('x axis'); ylabel('y axis'); zlabel('Error'); title('Error surface')
gi=input('Strike any key to continue......');
% Maximum fitting error
Maxfiterror = max(max(z-a))
Maxfiterror = 0.1116
Рис.2.17 Поверхня похибки
| 
Рис.2.18. Збіжність процесу
|
Залежно від ресурсів комп'ютера допуск похибки може бути зроблений більш строго, скажімо, 10-5.Збіжність тепер займає значно більше часу й показана нижче (рис.2.18).Повторна імітація процесу дає результат, показаний на рис.2.19.
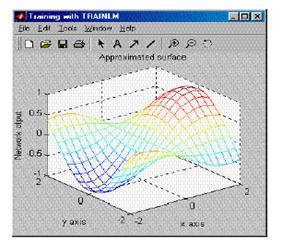Рис.2.19. Кінцевий результат відтворення поверхні
|
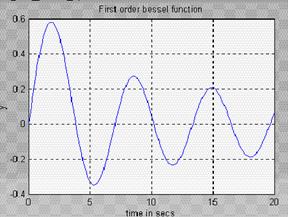Рис.2.20 Функція Бесселя 1-го порядку
|
ПРИКЛАД 3. Обчислити функції Бесселя J_ (t), які є рішенням диференціального рівняння
Використовуємо нейромережу зворотного поширення(backpropagation), щоб апроксимувати функцію Бесселя першого порядку - J1,a =1, якщо t Í [0,20].
a) Відтворимо графічно функцію - Plot J1(t).
b) Будемо змінювати структури для адаптації. Починаємо з двохшарової НМе. Можна також змінювати алгоритми навчання.
РІШЕННЯ:
1. Спочатку виконуємо генерацію даних,.MATLAB має Bessel-Функцію як убудовану функцію.
t=0:0.1:20; y=bessel(1,t);
plot(t,y)
grid
xlabel('time in secs');ylabel('y'); title('First order bessel function');
2. Даліі намагаємося пристосувати backpropagation-НМе для отриманих даних.Використовуємо алгоритм Levenberg-Marquardt.
P=t; T=y;
%Define network. First try a simple one
net=newff([0 20], [10,1], {'tansig','purelin'},'trainlm');
%Define parameters
net.trainParam.show = 50;
net.trainParam.lr = 0.05;
net.trainParam.epochs = 300;
net.trainParam.goal = 1 e-3;
%Train network
net1 = train(net, P, T);
TRAINLM, Epoch 0/300, MSE 11.2762/0.001, Gradient 1908.57/1 e-010
TRAINLM, Epoch 3/300, MSE 0.000417953/0.001, Gradient 1.50709/1 e-010
TRAINLM, Performance goal met.
% Simulate result
a= sim(net1,P);
%Plot result and compare
plot(P,a,P, a-T)
xlabel('time in secs');ylabel('Network output and error');
title('First order bessel function'); grid
Рис.2.21. Перше відтворення функції
| 
Рис.2.1.22. Похибка навчання
|
Похибка є досить істотною, для її зменшення спробуємо виконати дублювання вузлів на першому схованому шарі до 20 і збільшимо припустиму похибку до 10-4.Тренування перевищує 8 ітерацій
TRAINLM, Epoch 0/300, MSE 4.68232/0.0001, Gradient 1153.14/1 e-010
TRAINLM, Epoch 8/300, MSE 2.85284 e-005/0.0001, Gradient 0.782548/1 e-010
TRAINLM, Performance goal met.
Після графічного відтворення результату одержуємо таку фігуру.
Рис.2.23. Кінцевий вид відтвореної функції
| 
Рис.2.24. Simulink-Модель рівняння Ван-дер-Поля
|
Як видно з останнього рис., результат істотно поліпшений, хоча усе ще потрібне поліпшення, але це вже завдання до користувача
ПРИКЛАД 4. Досліджуємо, якщо це можливо, яким образом можна знайти модель НМе, що має таке ж поводження, як і процес, що описується рівнянням Ван-Дер-Поля
| 
|
або у формі простору станів-
Будемо використовувати різні функції активації. Застосуємо векторну нотацію для побудови НМе.
РІШЕННЯ:
Спочатку сконструюємо Simulink-Модель рівняння Ван-дер-Поля. Модель наведена нижче (рис.2.24). Викликається вона за допомогою функції vdpol. Нагадаємо, що початкові умови можуть бути визначені обчисленням інтегралів з використанням Simulink-Інтеграторів. Наприклад, початкова умова х1(0) = 2 встановлюється відкриттям відповідного інтегратора.
Рис.2.25. Установлення початкових умов
| 
Рис.2.26
|
Використовуємо початкові умови x1(0) = 1, x2(0) = 1.
% Define the simulation parameters for Van der Pol equation
% The period of simulation: tfinal = 10 seconds;
tfinal = 10;
% Solve Van der Pol differential equation
[t,x]=sim('vdpol',tfinal);
% Plot the states as function of time
plot(t,x)
xlabel('time (secs)'); ylabel('states x1 and x2'); title('Van Der Pol'); grid
gi=input(Strike any key...');
%Plot also the phase plane plot
plot(x(:,1),x(:,2)), title('Van Der Pol'),grid
gi=input(Strike any key...');
Рис.2.27
| 
Рис.2.28
|
% Now you have data for one trajectory, which you can use to teach a neural network
% Plot the data (solution). Observe that the output vector includes both
P = t';
T = x';
plot(P,T,'+');
title('Training Vectors');
xlabel('Input Vector P');
ylabel('Target Vector T');
gi=input('Strike any key...');
% Define the learning algorithm parameters, radial basis function network chosen
net=newff([0 20], [10,2], {'tansig','purelin'},'trainlm');
%Define parameters
net.trainParam.show = 50;
net.trainParam.lr = 0.05;
net.trainParam.epochs = 300;
net.trainParam.goal = 1 e-3;
%Train network
net1 = train(net, P, T);gi=input(' Strike any key...');
TRAINLM, Epoch 0/300, MSE 4.97149/0.001, Gradient 340.158/1 e-010
TRAINLM, Epoch 50/300, MSE 0.0292219/0.001, Gradient 0.592274/1 e-010
TRAINLM, Epoch 100/300, MSE 0.0220738/0.001, Gradient 0.777432/1 e-010
TRAINLM, Epoch 150/300, MSE 0.0216339/0.001, Gradient 1.17908/1 e-010
TRAINLM, Epoch 200/300, MSE 0.0215625/0.001, Gradient 0.644787/1 e-010
TRAINLM, Epoch 250/300, MSE 0.0215245/0.001, Gradient 0.422469/1 e-010
TRAINLM, Epoch 300/300, MSE 0.0215018/0.001, Gradient 0.315649/1 e-010
TRAINLM, Maximum epoch reached, performance goal was not met.
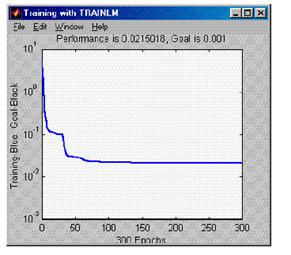Рис.2.29
| 
Рис.2.30
|
Мережна структура надзвичайно проста, що пояснює той факт, чому збіжність не досягнута. Розглянемо, як закриття мережного рішення виявиться в імітованому рішенні.
%Simulate result
a= sim(net1,P);
%Plot the result and the error
plot(P,a,P, a-T)
gi=input('Strike any key...');
Результат не може бути визнаний задовільним, тому необхідно почати спробу поліпшити його. Використання 20 вузлів на схованому шарі дає кращий результат.
Рис.2.31
|
Зробимо ще одну спробу вдосконалити рішення за рахунок застосування багатошарового персептрона. Використовуємо РБФ НМе із парамектром spread = 0.01.
net1=newrb(P,T,0.01);
%Simulate result
a= sim(net1,P);
%Plot the result and the error
plot(P, a-T,P,T)
Результат показаний на малюнку 1.31.
