Лабораторна робота № 36

 

ДОСЛІДЖЕННЯ ЕЛЕКТРИЧНИХ ВЛАСТИВОСТЕЙ
ПРОВІДНИКІВ ТА НАПІВПРОВІДНИКІВ

 

Мета роботи:

дослідити основні електричні характеристики провідників і на-півпровідників.

 

Перед виконанням роботи необхідно ознайомитись з такими питаннями курсу фізики.

1. Розподіл Фермі-Дірака. Рівень Фермі.

2 Електропровідність провідників та її залежність від темпера-тури.

3 Електропровідність напівпровідників та її залежність від температури.

4 Основні властивості терморезисторів.

 

ЗАВДАННЯ

 

1. Зняти вольт-амперну характеристику напівпровідникового терморезистора.

2. Дослідити залежність опору металевого провідника і напів-провідникового терморезистора від температури.

3. Визначити температурний коефіцієнт опору для провідника та напівпровідника, а також ширину забороненої зони.

 

ТЕОРЕТИЧНИЙ ВСТУП

 

Однією з основних електричних характеристик речовини є питома електропровідність s. Це фізична величина, яка є коефіцієнтом пропорційності між густиною струму і напруженістю електричного поля в законі Ома в диференціальній формі:

. (36-1)

 

Питомий опір є величина, обернено пропорційна , тобто

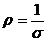. (36-2)

Залежно від величини всі речовини підрозділяють на три великі класи: провідники (добре проводять електричний струм), діелектрики (практично не проводять струм) і напів-провідники (займають проміжний інтервал між першими і дру-гими). Проте суттєвою особливістю провідників і напівпровід-ників є не стільки величина питомого опору, скільки характер залежності його від температури. Якщо у металів опір зростає, причому в широкому діапазоні температур лінійно, то у напів-провідників він швидко спадає за експоненціальним законом. На рис.5 представлені графіки температурної залежності опорів для деяких зразків Al та Ge.

 

 

Рис.5

Питому електропровідність речовини можна виразити через концентрацію вільних носіїв струму n, їхній заряд q і рухливість

 

носіїв u таким чином:

. (36-3)

Зонна теорія твердих тіл дає пояснення різної температурної залежності опорів металів і напівпровідників.

В металах валентна зона заповнена електронами не повністю. Відповідно до принципу Паулі на кожному енергетичному рівні

може розташовуватись два електрони

з протилежними спінами. Найвищий

рівень, який займають електрони при

температурі абсолютного нуля, назива-

ється рівнем Фермі (рис.6). В мета-

лах електронний газ є виродженим,

тобто його енергія практично не зале-

жить від температури, концентрація

носіїв n теж не змінюється. Рух елек-

тронів провідності під дією електрич-

ного поля буде можливим, якщо елек-

Рис.6 трони зможуть підніматись на більш

високі енергетичні рівні. Це матиме місце для електронів, що розташовані на рівні Фермі. Отже, рух електронів буде задаватись у першу чергу поведінкою електронів на рівні Фермі, які мають швидкість . Для електропровідності металів квантова теорія дає такий вираз:

, (36-4)

де е – заряд електрона, - довжина вільного пробігу фермієвих електронів, - ефективна маса електрона, в якій враховано складний квантовомеханічний характер взаємодії електронів провідності з періодичним полем кристалічної решітки. Отже, визначається величиною , яка обернено пропорційна темпера-турі Т через збільшення зіткнень електронів з вузлами криста-лічної решітки. Таким чином, дається пояснення лінійної залеж-ності r ~ T.

 

Температурним коефіцієнтом 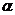опору називається відносна величина зміни опору при зміні температури на 1 К, тобто

, (36-5)

де - опір при температурі T, - зміна опору при збільшенні температури на .

Для металів 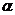є постійною величиною на досить широкому інтервалі температур, тому його можна підрахувати за форму-лою

, (36-6)

де R – опір при температурі T, - опір при температурі .

Тепер розглянемо особливості електропровідності напівпро-відників, обмежившись власними напівпровідниками.

У напівпровідників при температурі абсолютного нуля ва-лентна зона (ВЗ) заповнена повністю, зона провідності (ЗП) є вільною, їх розділяє заборонена зона (ЗЗ) завширшки < 3 еВ, а рівень Фермі проходить посередині забороненої зони (рис.7).

При Т = 0 в напівпровіднику вільних носіїв електричного

заряду нема, отже, електропровід-

ність відсутня. При зростанні тем-

ператури відбуваються переходи

електронів з ВЗ в ЗП, при цьому

виникають вільні носії заряду –

електрони в ЗП і дірки в ВЗ. Їх

концентрація є о днаковою і зале-

жить від температури за експо-

ненціальним законом, тобто

. (36-7)

Рис.7 Питома електропровідність напів-

провідника має дві складові – електронну і діркову:

. (36-8)

 

Рухливості електронів і дірок і 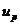слабко залежать від темпе-ратури за степеневим законом, тому, враховуючи залежність (36-7), матимемо експоненціальний закон зміни від темпера-тури

. (36-9)

Переходячи до опорів, згідно з формулою (36-2) одержимо екс-поненціальну залежність

, (36-10)

де - опір власного напівпровідника при . Таким чином, у напівпровідників опір зменшується при зростанні температури.

Залежність (36-10) зручно представляти графічно в напівло-гарифмічному вигляді, тобто

. (36-11)

В цьому випадку графік залежності представляє собою пряму лінію (рис.8). Тангенс кута нахилу графіку (36-11) є коефіцієнт при 1/ Т, тобто

, (36-12)

де k = 1,38×10 Дж/К – стала Больцмана.

 

Рис.8

Взявши дві довільні точки на графіку, знайдемо, що

 

. (36-13)

Підставляючи останній вираз у формулу (36-12), знайдемо ши-рину забороненої зони

. (36-14)

Температурний коефіцієнт опору 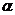для напівпровідника знай-демо за означенням (36-5), підставляючи похідну від виразу (36-10). В результаті нескладних математичних перетво-рень, враховуючи (36-14), одержимо

. (36-15)

Таким чином, для напівпровідника 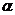є від’ємною величиною і при зростанні температури збільшується.

Напівпровідникові резистори, опір яких дуже чутливий до температури, одержали назву напівпровідникових терморезисто-рів (НТР) або термісторів. Вольт-амперна характеристика НТР на рис. 9 представлена у вигляді залежності напруги U від сили

струму I в напівпровіднику.

При невеликих струмах ця за-

лежність лінійна (ділянка 1),

тобто опір R залишається не-

змінним, виконується закон

Ома. При збільшенні струму

зростає розсіювана на НТР

потужність (), на-

півпровідник нагрівається,

його опір зменшується, що й

призводить до зменшення на-

Рис.9 пруги (ділянка 2).

Температурний коефіцієнт опору , вольт-амперна харак-теристика, а також величина В (або ) є основними характе-ристиками термісторів.

 

 

ОПИС ЛАБОРАТОРНОЇ УСТАНОВКИ

 

Функціональна схема лабораторної установки представлена на рис.10. Основними елементами схеми є:

 

 

 

 

Рис.10

Т – термостат з термометром;

Пр – провідник у вигляді спіралі з мідного або залізного дроту;

НТР – напівпровідниковий терморезистор (бусинковий терміс-
тор);

Л – лампочка, що є нагрівальним елементом;

R1 – міст ММВ для вимірювання опору провідника;

 

R2 – вбудований в корпусі установки міст для вимірювання опору терморезистора;

“R” – положення перемикача “Рід роботи” при вимірюванні опору НТР;

“V–A” - положення перемикача “Рід роботи” при знятті вольт-амперної характеристики НТР;

П – потенціометр;

Н – ключ ввімкнення нагріву;

М – мікросхема, що є стабілізатором напруги 5 В;

В – вольтметр;

А – амперметр;

К – корпус установки.

В термостаті розміщені досліджувані металевий провідник і напівпровідниковий терморезистор. Нагрівання здійснюється при ввімкненні лампочки Л за допомогою ключа Н. Вимірювання опорів провідника і напівпровідника виконується за допомогою окремих мостів постійного струму незалежно один від одного. Потенціометр П дозволяє змінювати силу струму в колі терміс-тора при знятті вольтамперної характеристики.

Температура нагріву не повинна перевищувати 80°С.