2018-01-08
962
Если проволоку (или стержень), закрепленную с одного конца, закручивать, прилагая пару сил с моментом М, то угол кручения по закону Гука будет равным φ =сМ, где с- коэффициент, зависящий от материала. Модуль кручения f определяется по формуле:
F=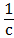 
= 
(6.1)
И показывает, какой момент нужно приложить, чтобы закрутить проволоку на угол в один радиан.
Модуль сдвига определяется из формулы
N= 
, (6.2)
Где 
-касательное напряжение; ω- угол сдвига. Размерность модуля сдвига такая же, как и у модуля Юнга (модуля упругости), - паскаль (Па).
Модули кручения и сдвига материала проволоки связаны соотношением
f=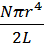 
, (6.3)
где r- радиус проволоки; L- её длина.
Если колеблющееся твердое тело совершает крутильные колебания, то к нему может быть применен основной закон вращательного движения:
M=J 
.
Если вращающий момент записать как 
, то получится уравнение вида
J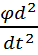 
= - 
.
Знак «-» в нём показывает, что вращательный момент всегда направлен так, чтобы уменьшить угол поворота φ. Если в этом уравнении произвести замену 
= 
, то получим уравнение колебаний:
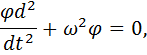
где ω-циклическая частота, связанная с периодом колебаний Т соотношением ω= 
. Тогда 
= 
, (6.4)
откуда
Т=2π 
,
где Т- период полного колебания маятника.
Для того, чтобы из этого выражения найти f, необходимо исключить неизвестный момент инерции J. Измерив периоды колебаний маятника при двух различных положениях грузов:
=2π 
и 
=2π 
,
получим:
= 
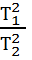(6.5)
Момент инерции крутильного маятника можно представить как сумму моментов инерции грузов – 2m 
и системы «стержень- проволока» - j. Для двух положений груза имеем:
=2m + j и 
= 2m 
+j.
Неизвестная величина j исключается вычитанием 
:
- = 2m(
).
Подставив в эту формулу значение = 
из уравнения (6.5), получим
= 
.
Теперь из выражения (6.4) находим модуль кручения:
f=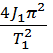 
= 
Зная расстояние от центров тяжести грузов до оси вращения и их массу, по формуле (6.3) вычисляем модуль сдвига:
N= 
(6.6)
