Метод наискорейшего спуска. Название метода можно было бы понимать буквально, если бы речь шла о минимизации целевой функции

Название метода можно было бы понимать буквально, если бы речь шла о минимизации целевой функции. Тем не менее по традиции такое название используется и при решении задачи на максимум.

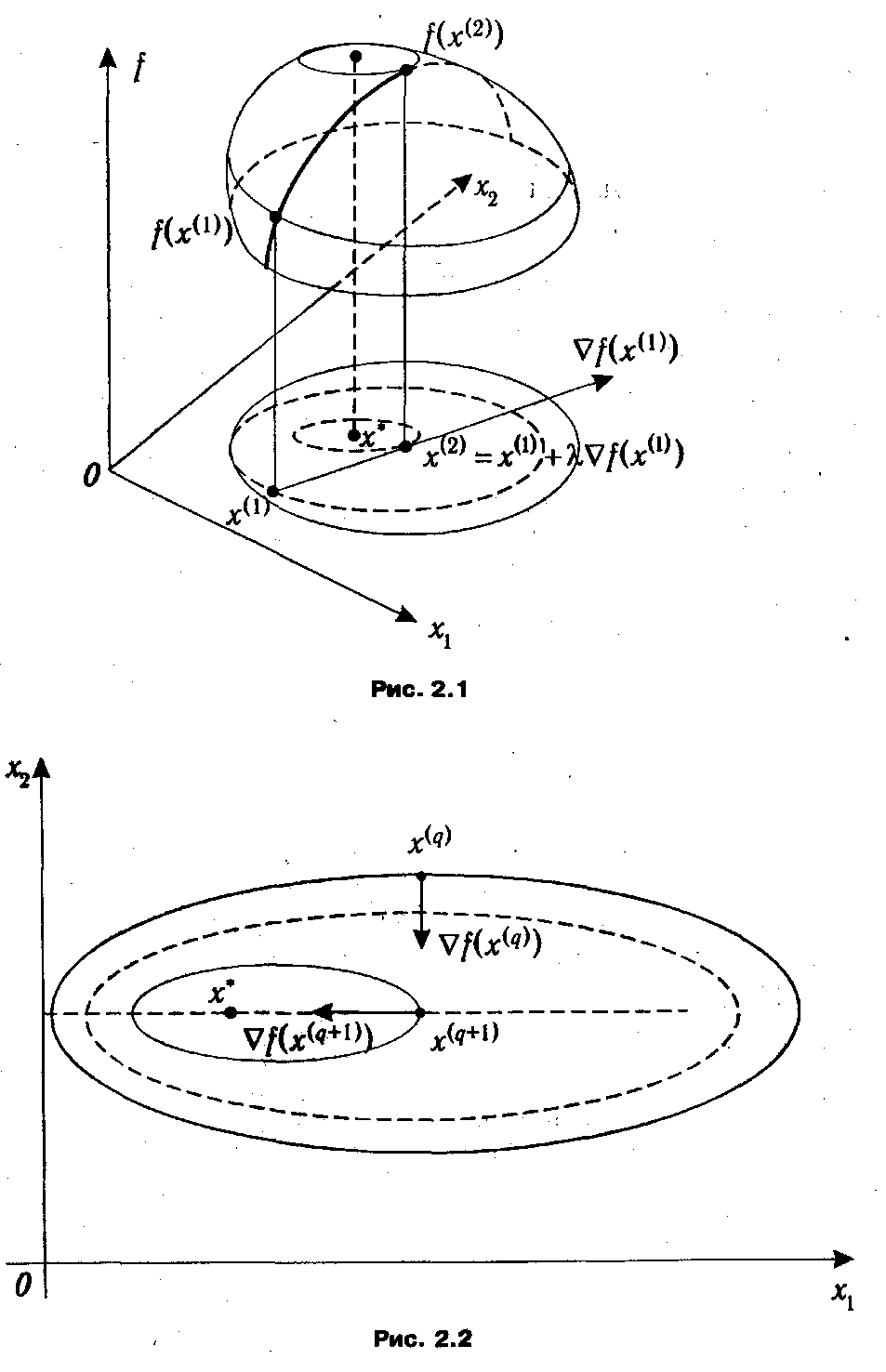
Пусть f(x)=f(x ₁ ,x ₁ ,...x_n) —дифференцируемая функция, заданная на Rⁿ, а х ⁽ ^q ⁾ = (x ₁⁽ ^q ⁾ ,x ₂⁽ ^q ⁾ ,...,x_n ⁽ ^q ⁾) — некоторая текущая точка. Оговоримся, что каких-либо общих рекомендаций, касающихся выбора исходной точки (или, как еще говорят, начального приближения) х ⁽⁰⁾, не существует, однако по возможности она должна находиться близко от искомого оптимального плана х *. Как уже говорилось выше, если х ⁽ ^q ⁾— нестационарная точка (т. е. | f (x ⁽ ^q ⁾)|>0), то при движении в направлении f (x ⁽ ^q ⁾) функция f(х) на некотором промежутке обязательно будет возрастать. Отсюда возникает естественная идея такого выбора шага, чтобы движение в указанном направлении продолжалось до тех пор, пока возрастание не прекратится. Для этого выразим зависимость значения f(x) от шагового множителя λ > 0. полагая х = х⁽ ^q ⁾ + λ f (x ⁽ ^q ⁾)

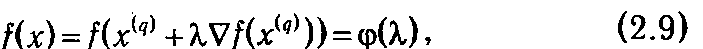
или, в координатной форме,

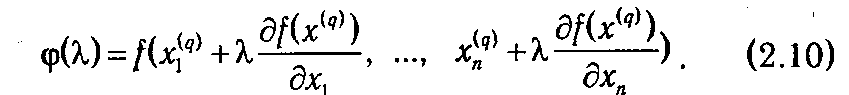
Чтобы добиться наибольшего из возможных значений f при движении по направлению f (x ^(q)), нужно выбрать такое значение 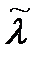, которое максимизирует функцию φ(λ) (φ(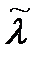)= max(φ(λ)). Для вычисления 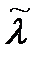, используется необходимое условие экстремума d φ(λ)/ d λ = 0. Заметим, что если для любого λ>0 d φ(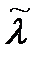)/ d λ> 0, то функция f(х) не ограничена сверху (т. е. не имеет максимума). В противном случае, на основе (2.10) получаем

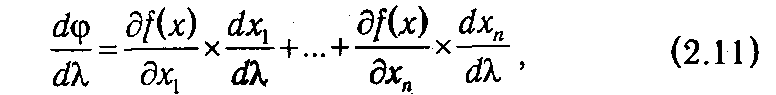
что, в свою очередь, дает

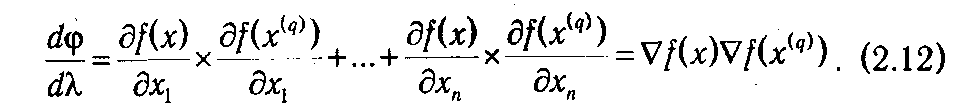
Если считать, что следующая точка х ⁽ ^q⁺ ¹⁾ соответствует оптимальному значению λ=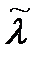, то в ней должно выполняться условие d φ(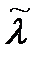)/ d λ = 0, и 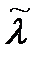следует находить из условия f (x ⁽ ^q ⁺¹⁾) f (x ⁽ ^q ⁾)=0 или

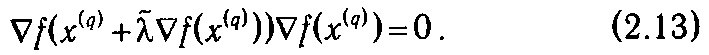
Условие (2.13) означает равенство нулю скалярного произведения градиентов функции f точках x ⁽ ^q ⁺¹⁾ и x ⁽ ^q ⁾. Геометрически оно может быть интерпретировано как перпендикулярность векторов градиентов функции f в указанных точках, что и показано на рис. 2.2. Продолжая геометрическую интерпретацию метода наискорейшего спуска, отметим, что в точке x ⁽ ^q ⁺¹⁾ вектор f (x ⁽ ^q ⁺¹⁾), будучи градиентом, перпендикулярен линии уровня, проходящей через данную точку. Стало быть, вектор f (x ⁽ ^q ⁾) является касательным к этой линии. Итак, движение в направлении градиента f (x ⁽ ^q ⁾) следует продолжать до тех пор, пока он пересекает линии уровня оптимизируемой функции.

После того как точка x ⁽ ^q ⁺¹⁾ найдена, она становится текущей для очередной итерации. На практике признаком достижения стационарной точки служит достаточно малое изменение координат точек, рассматриваемых на последовательных итерациях. Одновременно с этим координаты вектора Δ f (x ⁽ ^q ⁾) должны быть близки к нулю.

Метод дробления шага

Для нахождения шага λ в методе наискорейшего спуска требуется решить уравнение (2.13), которое может оказаться достаточно сложным. Поэтому часто ограничиваются «подбором» такого значения λ, что φ(λ) > φ(0). Для этого задаются некоторым начальным значением λ₁, (например, λ₁=l) и проверяют условие φ(λ₁) >φ(0). Если оно не выполняется, то полагают

λ₂ = 1/2 λ₁

и т. д. до тех пор, пока не удается найти подходящий шаг, с которым переходят к следующей точке x ⁽ ^q ⁺¹⁾. Критерий завершения алгоритма, очевидно, будет таким же, как и в методе наискорейшего спуска.

2.1.4. Оптимизационные задачи для выпуклых функций. Общим недостатком рассмотренных выше методов безусловной оптимизации было, с одной стороны, то, что они позволяют отыскивать только точки, подозрительные на локальный экстремум, а с другой — то, что найденные решения могут существенно зависеть от начального приближения. Поиск глобального оптимума подразумевает перебор найденных точек, который,

в случае градиентных методов, может быть осуществлен за счет подбора соответствующих начальных приближений х ⁽⁰⁾.

Однако существует один класс функций, для которых градиентные методы приводят к нахождению глобального оптимума. Это выпуклые функции.

F Функция f(x) = f (x ₁, x ₂, …, x_n) называется выпуклой в области D, если для любых двух точек х ⁽¹⁾,

х ⁽²⁾Î D и любого λ Î [0,1] выполняется неравенство

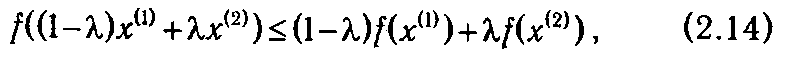
если же

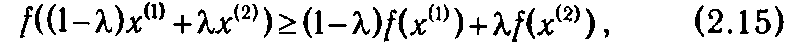
то функция называется вогнутой.

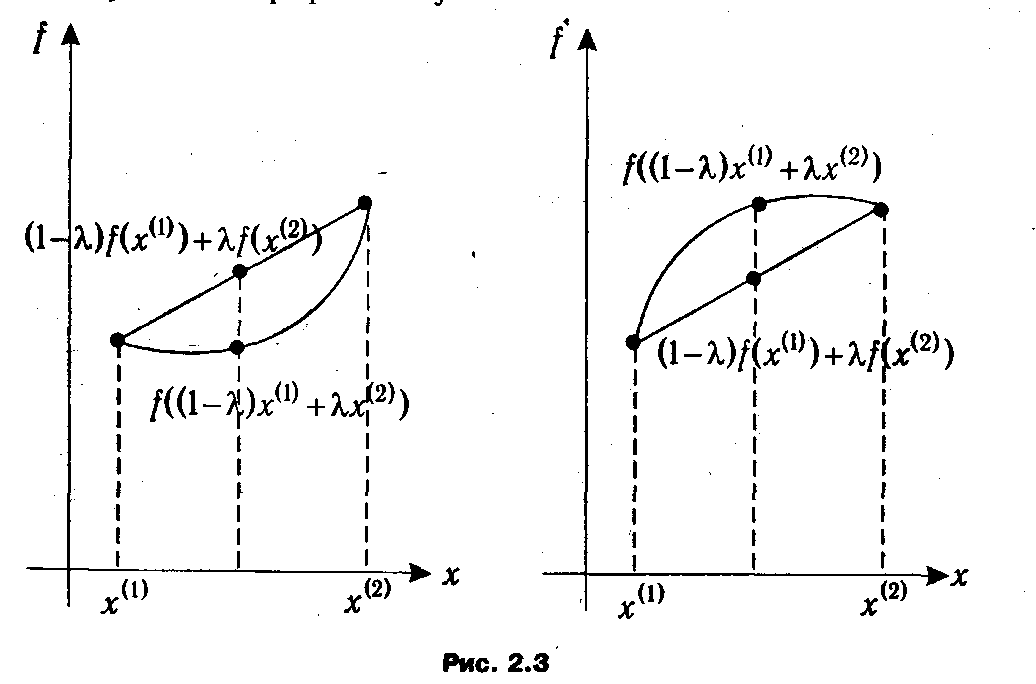
Геометрический смысл понятий выпуклости и вогнутости для случая функции одной переменной представлен на рис. 2.3. Из него, в частности, видно, что график выпуклой функции лежит ниже отрезка, соединяющего точки (х ⁽¹⁾, f (x (¹⁾)) и (х ⁽²⁾, f (x ⁽²⁾)), а график вогнутой — выше.

Можно доказать, что достаточным условием выпуклости функции f (x ₁, x ₂, …, x_n) является положительная определенность матрицы

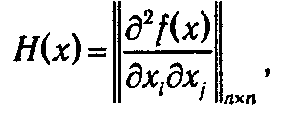
называемой также матрицей Гессе, во всех точках х Î D. Соответственно, достаточным условием вогнутости является отрицательная определенность матрицы Гессе. В частности, для функций одной переменной достаточным условием выпуклости (вогнутости) является выполнение неравенства f ⁿ (x)≥0 (f ⁿ (x)≤0).

Как следует из геометрической интерпретации, для выпуклой функции локальный экстремум, если он существует, совпадает с глобальным. Справедлива теорема.

Теорема 2.2. Если f(x) выпуклая (вогнутая) на Rⁿ функция и f (x *) = 0, то х* — точка глобального минимума (максимума).

Доказательство.

Доказательство достаточно провести для случая вогнутой функции, т. к. для противоположного случая оно будет абсолютно аналогичным с точностью до знака.

Пусть х — произвольная точка, отличная от точки х *. Тогда, для любого λ Î [0,1], в силу вогнутости функции f(x) будет выполняться

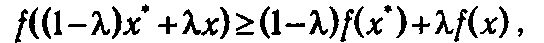
из чего следует

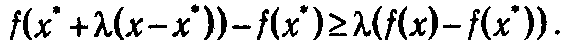
Если ввести вектор l = х - х * и обозначить Δ х = λ(x – х*) = λ l, то длина вектора Δ х будет равна ||Δ x ||=λ|| l ||. Следовательно,

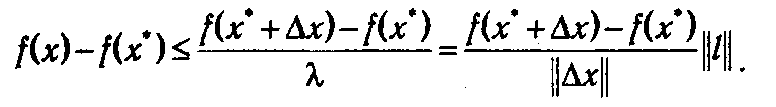
Устремив λ → 0 и учитывая, что вектор l сонаправлен с Δ х, получим

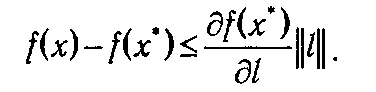
По условию теоремы f (x *)=0. Это означает, что для любого вектора l (а, стало быть, для любой точки х) согласно формуле, выражающей производную по направлению через градиент,

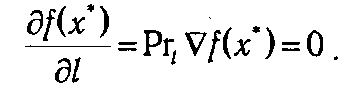
Следовательно, для любой точки х, не равной х *, справедливо неравенство f(x)-f(x)≤ 0 <=> f(x)≤ f(x * ), т.е. х * — точка глобального максимума. A

Поскольку выпуклые функции обладают столь «полезными» оптимизационными качествами, они занимают исключительно важное место в теории исследования операций. Соответствующий раздел получил название выпуклого программирования, а общая задача выпуклого программирования формулируется как проблема поиска максимума вогнутой (минимума выпуклой) функции на выпуклом множестве.

2.1.5. Метод допустимых направлений. Данный метод также называется методом возможных направлений или же по имени автора—методом Зойтендейка, см. [16]. Его основную идею будет удобно продемонстрировать на примере ЗНП с ограничениями в форме неравенств:

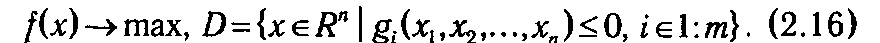
В указанном методе так же, как и в градиентных методах, находится последовательность точек х ⁽⁰⁾ х ⁽¹⁾,..., х ⁽ ^q ⁾..., таких, что f (х ⁽ ^q ⁺¹⁾) ≥ f (x ⁽ ^q ⁾) *. При этом переход от точки x ^(q)) к точке х ^{(q +1)}) происходит по некоторому выбранному направлению s ^(q) с шаговым множителем λ _q:

* Так как в данных методах при переходе к очередной рассматриваемой точке происходит улучшение значения целевой функции (в частности, для задачи минимизации — уменьшение), их также называют релаксационными методами.

По отношению к векторам, задающим направления перемещения, вводятся два фундаментальных понятия.

F Направление s называется допустимым (возможным) в точке x ⁽ ^q ⁾Î D, если существует такое

λ > 0, что x ⁽ ^q ⁺¹⁾= x ⁽ ^q ⁾ + λ s Î D.

F Направление s называется прогрессивным в точке x ⁽ ^q ⁾ Î D, если существует такое λ >0, что

f (x ⁽ ^q ⁾ + λ s)> > f (x ⁽ ^q ⁾) для задачи максимизации и f (x ⁽ ^q ⁾ + λ s) < f (x ⁽ ^q ⁾) для задачи минимизации.

На основе данных определений достаточно просто сформулировать критерий проверки оптимальности точки (так называемый критерий оптимальности в терминах допустимых и прогрессивных направлений):

F точка х* является оптимальным планом задачи (2.16), если в ней ни одно допустимое

направление не является прогрессивным.

В алгоритме метода допустимых направлений правила выбора точки х ⁽ ^q ⁺¹⁾, к которой происходит очередной переход, различаются в зависимости от того, где находится текущая точка х ⁽ ^q ⁾. Принципиально возможны две ситуации.

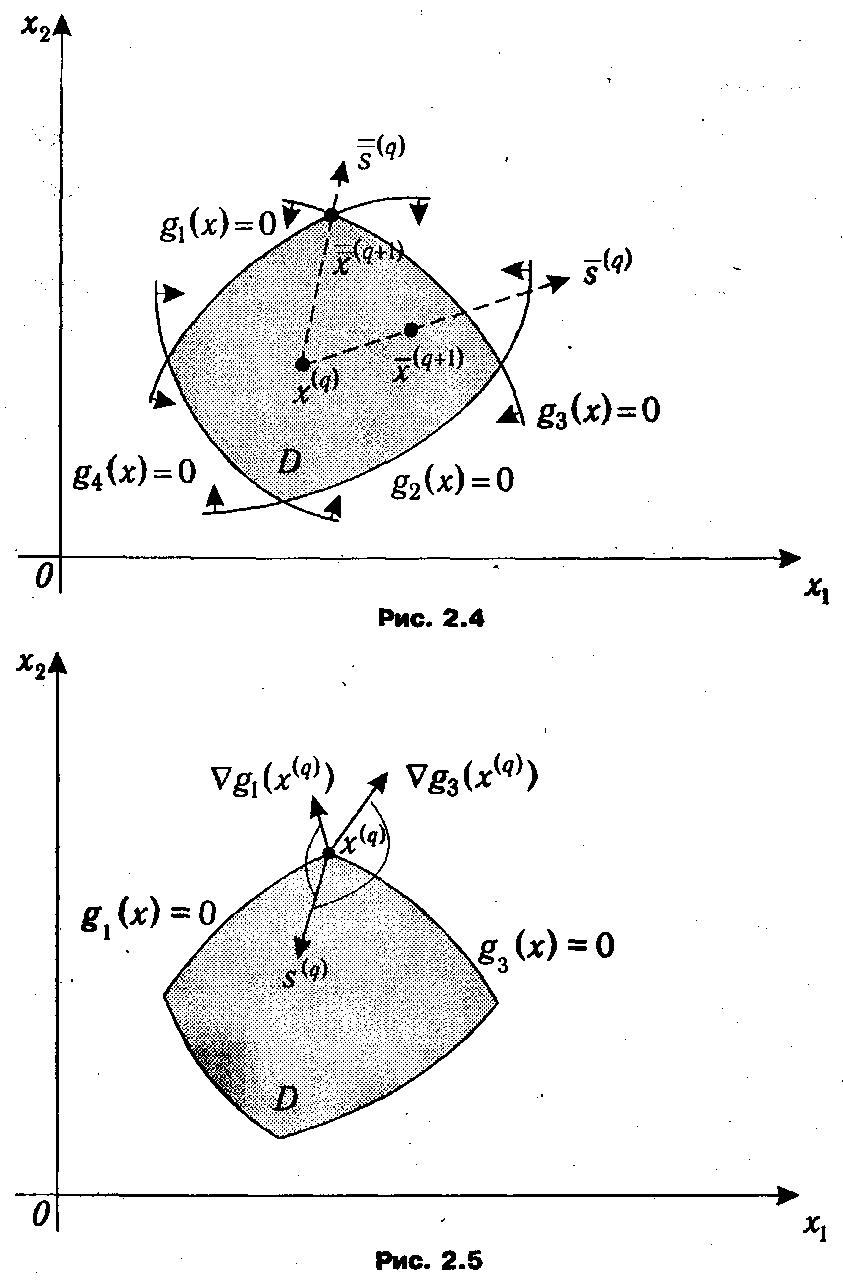
1°. Точка х ⁽ ^q ⁾ лежит внутри области D, т. е. для всех i Î 1: m g_i (х ⁽ ^q ⁾) < 0 (см. рис. 2.4). Очевидно, что для внутренней точки любое направление будет допустимым (при выборе достаточно малого шага), поэтому естественным представляется движение в сторону «гарантированного» возрастания значения функции, а именно в направлении градиента. Значит, для внутренней точки х ⁽ ^q ⁾ целесообразно выбрать s ⁽ ^q ⁾= f (х ⁽ ^q ⁾).

Шаговый множитель λ _q выбирается так, чтобы, с одной стороны, новая точка х ⁽ ^q ⁺¹⁾ принадлежала D, а с другой — значение целевой функции в ней f (х ⁽ ^q ⁺¹⁾) было как можно большим.

С этой целью сначала найдем промежуток [0, 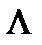] из условия 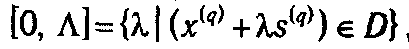для чего необходимо решить систему неравенств:

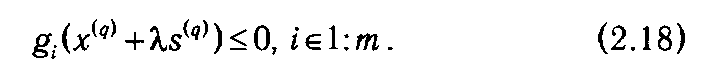
Зная промежуток [0, 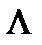], определяем значение шагового множителя λ _q из условия максимизации значения функции в направлении s⁽^q⁾:

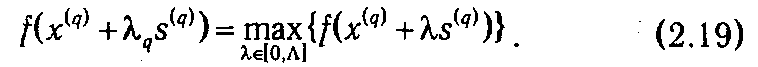
Вновь найденная точка x ⁽ ^q ⁺¹⁾ может находиться или внутри области D, или на ее границе. В первом случае (на рис. 2.4 ему соответствует точка ⁽ ^q ⁺¹⁾ переходим к началу данного пункта и повторяем вышеописанные действия, а во втором (точка ⁽ ^q ⁺¹⁾ на рис. 2.4) — действуем по рассматриваемой далее схеме.

2°. Точка x ^(q) находится на границе области (см. рис. 2.5). Это означает, что одно или несколько неравенств из системы ограничений задачи (2.16) выполняются как строгие равенства: g_i (x ⁽ ^q ⁾) = 0. Например, на рис. 2.5 и g ₁(x ⁽ ^q ⁾) = 0 и g ₃(x ⁽ ^q ⁾) = 0.

Ограничение, которое в текущей точке выполняется как равенство, называют активным. Множество номеров активных ограничений в точке x ⁽ ^q ⁾ будем обозначать как I (x ⁽ ^q ⁾). В примере, изображенном на рис. 2.5, I (x ⁽ ^q ⁾) = {1, 3}. Также из рисунка видно, что все допустимые направления, исходящие из точки x ⁽ ^q ⁾, должны образовывать тупые углы с векторами градиентов функций, задающих активные ограничения в данной точке. Последнее условие может быть выражено через задание ограничений на значения скалярных произведений вектора направления s на градиенты функции ограничений:

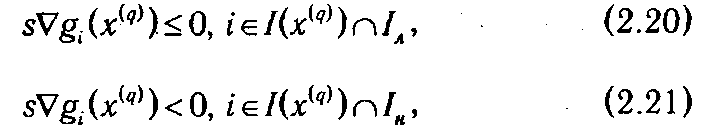
где I_л — множество номеров индексов линейных ограничений, I_н — множество номеров индексов нелинейных ограничений. Соответственно, I (x ⁽ ^q ⁾)◠ I_л —номера линейных активных ограничений, а I (x ⁽ ^q ⁾)◠ I_н — номера нелинейных активных ограничений. Отличие условий (2.20) от условий (2.21) заключается в том, что в случае линейного ограничения направление, образующее прямой угол с градиентом ограничивающей функции (т. е. их скалярное произведение равно нулю), будет заведомо допустимым, а в случае нелинейного ограничения — возможно, нет.

Все возможные направления в точке x ⁽ ^q ⁾ образуют так называемый конус допустимых направлений, и из них для следующего перехода, очевидно, нужно выбрать прогрессивное. Если такового не существует, то согласно сформулированному выше критерию точка x ⁽ ^q ⁾ является оптимальной! Для ускорения максимизации функции желательно, чтобы угол между искомым допустимым прогрессивным направлением s ⁽ ^q ⁾ и градиентом целевой функции ∇ f (x ⁽ ^q ⁾) был как можно меньше или, что то же самое, как можно большей была бы проекция s на ∇ f (x ⁽ ^q ⁾) (при условиях нормировки вектора s ⁽ ^q ⁾). Иными словами, желательно, чтобы неравенство s ⁽ ^q ⁾∇ f (x ⁽ ^q ⁾)+σ≥0 выполнялось при минимально возможном σ ∈ R. Тогда задачу отыскания наилучшего допустимого прогрессивного направления s ⁽ ^q ⁾можно свести к задаче минимизации параметра σ:

при условиях

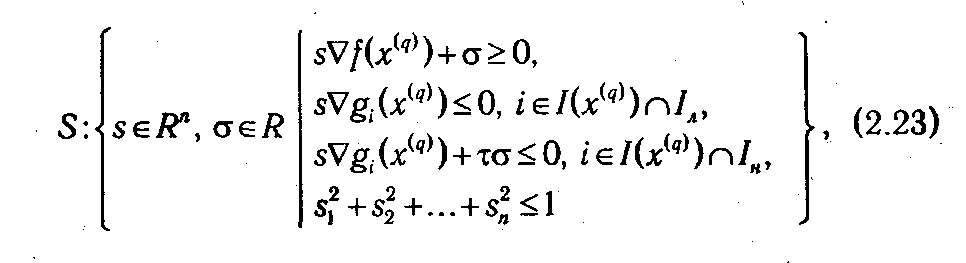
где s ₁² +s ₂² +...+s_n ², ≤ l —условие нормировки, обеспечивающее ограниченность решения;

τ — некоторое достаточно малое число, характеризующее «строгость» выполнения неравенств.

В отличие от всех остальных, последнее условие в системе (2.23) является нелинейным, что существенно усложняет процесс решения задачи (2.22)-(2.23). Поэтому на практике для определения направления s ⁽ ^q ⁾ (возможно, не лучшего) переходят от данной задачи к задаче линейного программирования путем замены указанных выше условий нормировки на ограничения вида –l ≤ s_j, ≤ 1:

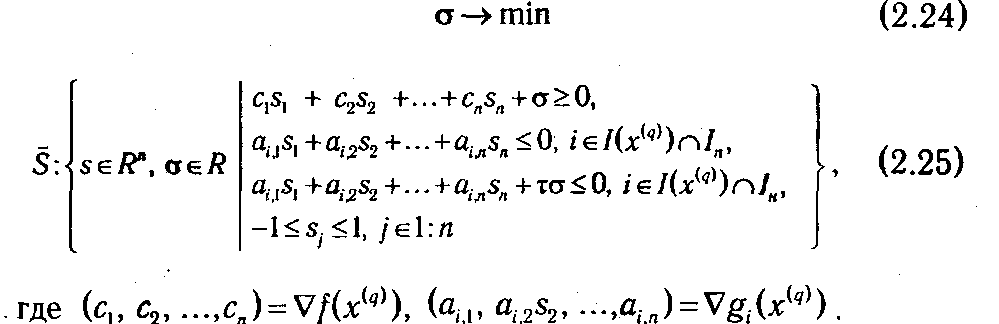
После того как прогрессивное направление s ⁽ ^q ⁾ найдено, шаговый множитель определяется по методу, описанному в п. 1°.

В заключение отметим, что при практических расчетах алгоритм завершается при достижении такой точки х *, в которой |∇ f (x *)|<ε, где ε —достаточно малое число.

Представляется полезным обратить внимание читателя и на то, что применяемый для решения задач линейного программирования симплекс-метод может быть рассмотрен как частный случай метода допустимых направлений. В частности, этап выбора столбца, вводимого в очередной базис, соответствует определению допустимого прогрессивного направления. Более подробно о такой концепции симплекс-метода можно прочесть в [1].

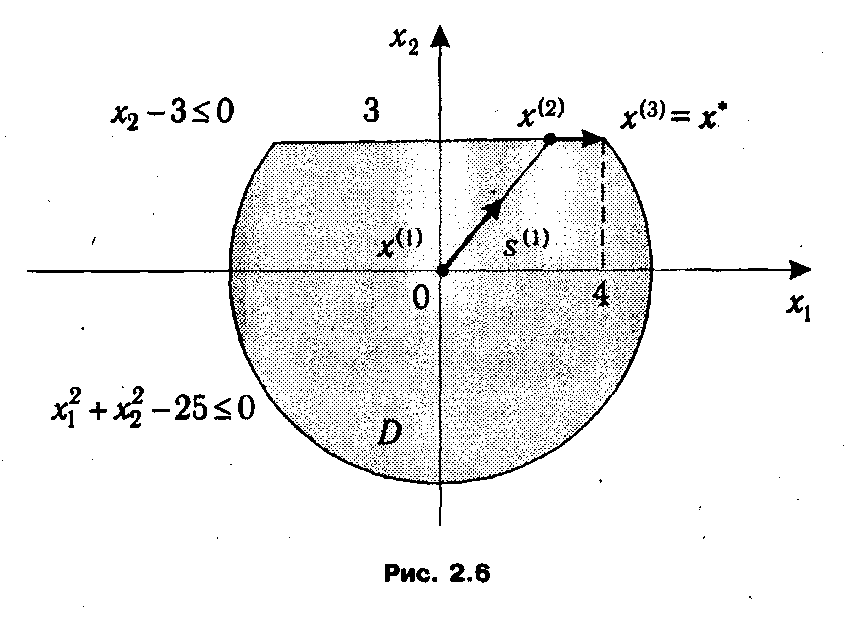
2.1.6. Пример решения ЗНП методом допустимых направлений. Рассмотрим процесс применения метода допустимых направлений на конкретном примере. Пусть дана ЗНП:

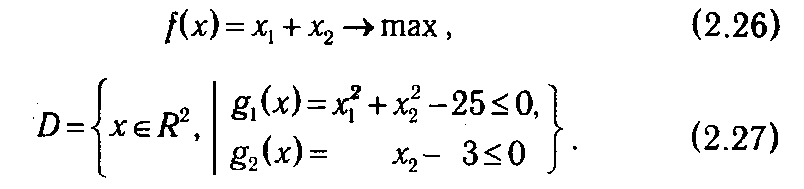
Итерация 1. В качестве начального приближения возьмем точку х ⁽¹⁾ = (0,0). Нетрудно заметить, что она удовлетворяет системе неравенств (2.27), т. е. х ⁽¹⁾ ∈ D. Для х ⁽¹⁾ все неравенства выполняются как строгие, т. е. множество индексов активных ограничений I (х ⁽¹⁾) = ∅. Следовательно, в х ⁽¹⁾ любое направление является допустимым, и нам остается определить, с каким шагом λ₁ можно двигаться вдоль градиента целевой функции s ⁽¹⁾ = ∇ f (x ⁽¹⁾)=(1, 1). Система неравенств типа (2.18), из решения которых определяется интервал допустимых значений для λ, для данной задачи примет вид:

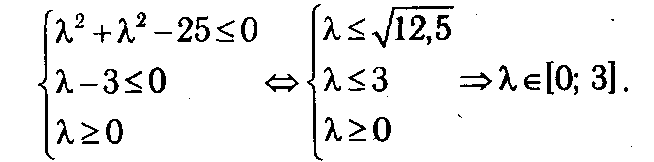
Тогда

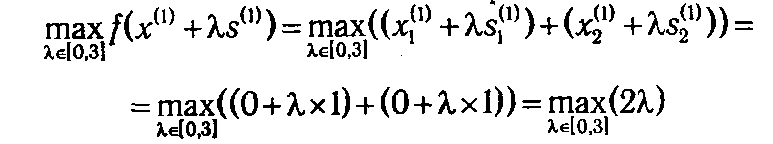
достигается при λ₁ = 3. Отсюда получаем следующую точку

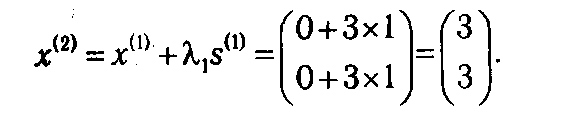
Итерация 2. Путем подстановки координат точки x ⁽²⁾ в (2.27) определим множество активных ограничений в точке x ⁽²⁾: I (x ⁽²⁾)={2}. Соответственно, задача (2.24) - (2.25), которую требуется решить для определения допустимого прогрессивного направления s ⁽²⁾ с учетом того, что ∇ f (x ⁽²⁾)=(1, 1) и ∇ g ₂(x ⁽²⁾)= (0, 1) примет вид:

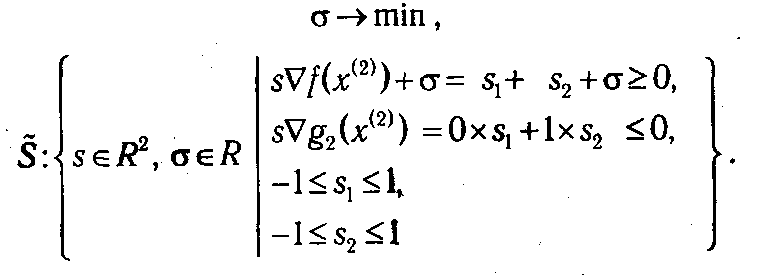
В данном случае оптимальный план ЗЛП находится довольно просто и равен (σ, s ₁, s ₂)* =(-1, 1, 0). Отбросив дополнительную переменную σ, получаем вектор s ⁽²⁾ = (1,0), т. е. очередная точка будет определяться как

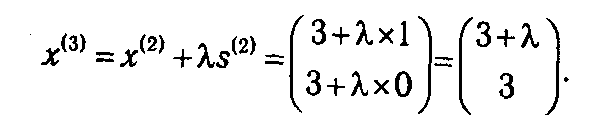
Действуя по аналогии с предыдущей итерацией, для определения промежутка допустимых значений шагового множителя λ составляем систему неравенств (2.18):

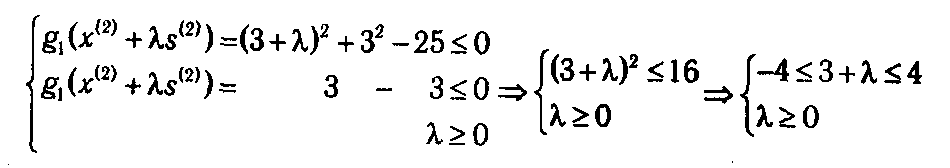
Окончательно имеем λ ∈ [0; 1].

Тогда

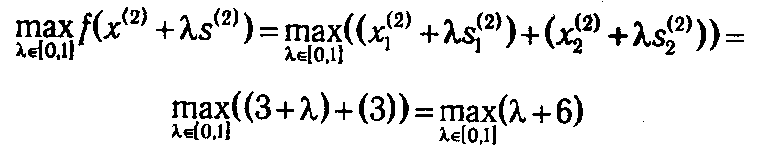
достигается при λ₂=1. Отсюда получаем следующую точку x ⁽³⁾= (3,4).

Итерация 3. В точке x ⁽³⁾множество активных ограничений будет иметь вид I (x ⁽³⁾)={1,2}. Найдем значения градиентов: ∇ f (x ⁽³⁾) = (1, 1), ∇ g ₁(x ⁽³⁾) = (2 x ₁⁽³⁾, 2 x ₂⁽³⁾) = (8, 6) и ∇ g ₂(x ⁽²⁾) = (0,1).

Задача определения допустимого прогрессивного направления (2.24)-(2.25) будет иметь вид:

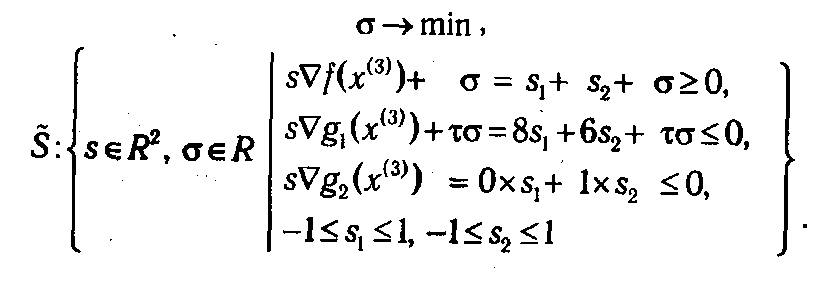
Значение τ из практических соображении следует брать достаточно малым, например τ = 0,001. Опуская решение данной задачи, приведем интересующие нас компоненты ее оптимального плана: s ⁽³⁾ = (0,0). Итак, не существует прогрессивного направления, исходящего из точки х ⁽³⁾ Таким образом, оптимальный план рассматриваемой задачи (2.26)-(2.27) х * = (4,3), а максимальное значение целевой функции f * = х ₁⁽³⁾ + х ₂⁽³⁾ = 7.