Для случая построения одного кратчайшего покрытия

Словесное описание алгоритма:

0. Считаем исходную таблицу покрытий текущей, а множество ядерных строк – пустым;

1. Находим ядерные строки, запоминаем множество ядерных строк. Текущую ТП сокращаем: вычеркиваем ядерные строки и все столбцы, покрытые ими;

2. Вычеркиваем антиядерные строки;

3. Вычеркиваем поглощающие столбцы;

4. Вычеркиваем поглощаемые строки;

5. Если в результате выполнения п.1-4 текущая ТП изменилась, снова выполняем п.1, иначе преобразования заканчиваем.

Получаются два результата: множество ядерных строк и ЦО ТП.

В случае построения минимального покрытия

При этом изменяется только п.4 алгоритма, который формулируется следующим образом: вычеркиваются поглощаемые строки, веса которых не меньше весов соответствующих поглощающих строк.

3. При условии построения всех безызбыточных покрытий

В этом случае п.4 не выполняется – нельзя вычеркивать никакие поглощаемые строки.

Алгоритм приближенного решения задачи о покрытии

 

Покрытие, близкое к кратчайшему, даёт следующий алгоритм преобразования ТП; основанный на методе “ минимальный столбец – максимальная строка ”.

0. Исходная таблица считается текущей преобразуемой ТП, множество строк покрытий – пусто;

1. В текущей таблице выделяется столбец с наименьшим числом единиц. Среди строк, содержащих единицы в этом столбце, выделяется одна с наибольшим числом единиц. Эта строка включается в покрытие, текущая таблица сокращается вычеркиванием всех столбцов, в которых выбранная строка имеет единицу.

2. Если в таблице есть невычеркнутые столбцы, то выполняется п. 1, иначе – покрытие построено.

Примечание. При подсчёте числа единиц в строке учитываются единицы в невычеркнутых столбцах.

2.6. Задачи для самостоятельной работы

 

1. Сократить до циклического остатка (ЦО) заданную ТП с помощью теорем 2.3-2.7 с гарантией построения одного кратчайшего покрытия.

2. Для полученного в предыдущем пункте ЦО построить кратчайшие и минимальные покрытия методом граничного перебора (цены для каждой строки задаются преподавателем индивидуально).

3. Решить задачу о покрытии методом минимального столбца - максимальной строки.

4. Сравнить полученные решения и сделать выводы.

1

2

А

А

Б

Б

В

В

Г

Г

Д

Д

Е

Е

Ж

Ж

З

З

3

4

А

А

Б

Б

В

В

Г

Г

Д

Д

Е

Е

Ж

Ж

З

З

5

6

А

А

Б

Б

В

В

Г

Г

Д

Д

Е

Е

Ж

Ж

З

З

АЛГОРИТМЫ НА ГРАФАХ

Цель практического занятия по данной теме - освоение идей основных алгоритмов на графах и приобретение навыков в использовании этих алгоритмов.

Общие положения

Графом G =(X, E) называется совокупность двух конечных множеств: множества точек, которые называются вершинами (Х ={ x₁, …, x_n })и множества связей в парах вершин ((x_i, x_j)Î E), которые называются дугами или ребрами в зависимости от наличия или отсутствия направленности связи.

Ребром называются две встречные дуги (x_i, x_j) и (x_j, x_i). На графе они изображаются одной линией без стрелки (рис. 3.1). Ребро, у которoго концевые вершины совпадают, называются петлей; то же относится и к дуге.

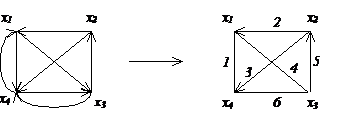
Рис. 3.1

Если на каждом ребре задаётся направление, то граф (X, E) называется о риентированным. В противном случае граф называется неориентированным.

Две вершины, являющиеся концевыми для некоторого ребра или некоторой дуги, называются смежными. Вершина и ребро (дуга) называются инцидентными друг другу, если вершина является для этого ребра (дуги) концевой точкой. Соответственно, граф может быть представлен матрицей смежности либо матрицей инцидентности.

Матрицей смежности называется прямоугольная таблица, у которой число строк и число столбцов одинаково и равно числу вершин. Элементы матрицы задаются следующим образом: “1” отмечается наличие соответствующей дуги (направление принимается от буквы, именующей строку, к букве, именующей столбец), “0” - отсутствие связи вершин; “1” на главной диагонали таблицы означает наличие петли на графе.

Матрицей инцидентности называется прямоугольная таблица с числом строк, равным числу вершин графа, и с числом столбцов, равным количеству рёбер (дуг) графа. Элементы матрицы a_ij задаются следующим образом: “1” ставится в случае, если вершина x_i инцидентна ребру (x_i, x_j), “0” - в противном случае.

Пример 3.1. На рис. 3.1 изображён граф, имеющий четыре вершины X ={ x₁, x₂, x₃, x₄ }, четыре дуги (x₁, x₃), (x₂, x₁), (x₂, x₃), (x₃, x₂) и два ребра (x₁, x₄), (x₄, x₅). Для вершины x1 смежными являются вершины: x₂, x₃ и x₄, а инцидентными - дуги (x₁, x₃), (x₂, x₁) и ребро (x₁, x₄). Матрица смежности представлена табл. 3.1, а матрица инцидентности – табл. 3.2.

Таблица 3.1 Таблица 3.2

G

x1

x2

x3

x4

G

x1

x1

x2

x2

x3

x3

x4

x4

Взвешенным называется граф, если задана функция веса l_ij на дугах графа, которая характеризует, например, длину дуги (x_i, x_j), время пребывания на дуге, пропускную способность дуги и т. д.; чаще всего l_ij ³ 0.

Функция веса задаётся в матричном виде (с - конечное число):

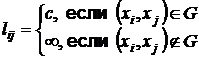; (3.1)

тогда в матрице смежности вместо 1 ставится c.

Для ориентированного графа определяются следующие понятия:

1. Исход вершины E (x_i) - множество вершин x_j, таких, что (x_i, x_j)Î E.

2. Вход вершины E ^-1(x_i) - множество вершин x_i, таких что (x_j, x_i)Î E.

3. Степень исхода - мощность S (x_i) =½ E (x_i)½ множества исхода.

4. Степень входа - мощность S ^-1(x_i)=½ E ^-1(x_i)½ множества входа.

Для графа (рис. 3.1) рассмотрим исходы и входы вершин x₁ и x₄. Имеем:

E (x₁)= { x₃, x₄ }; (x₁, x₃), (x₁, x₄)Î E; E (x₄)= { x₁, x₃ }; (x₄, x₁), (x₄, x₃)Î E;

E ^-1(x₁)={ x₂, x₄ }; (x₂, x₁), (x₄, x₁)Î E;

E ^-1(x₄)={ x₁, x₂, x₃ }; (x₁, x₄), (x₂, x₄), (x₃, x₄)Î E.

Для тех же вершин x₁ и x₄ степени исхода и входа соответственно равны S (x₁)=2, S (x₄)=2; S^{- 1}(x₁)=2, S^{- 1}(x₄)=3.

Для неориентированного графа степень S (x_i)=½ E (x_i)½ вершины x_i равна числу рёбер, инцидентных этой вершине.