2018-01-08
3228
Взаимное притяжение всех тел Вселенной называется всемирным тяготением.
Сила, с которой все тела притягиваются друг к другу, называется силой всемирного тяготения(или гравитационной силой).
Английский ученый И. Ньютон установил закон всемирного тяготения: Все тела притягиваются друг к другу с силой прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.
G – коэффициент пропорциональности, который называется гравитационной постоянной.
Опытным путем английский ученый Генри Кавендиш (1731–1810) в 1798 году установил, что 
.
Примечание:
1. Закон всемирного тяготения в форме, записанной выше, справедлив для материальных точек, а так же для однородных сфер и шаров (в этом случае r – расстояние между центрами сфер или шаров).
2. Массы, входящие в закон всемирного тяготения, характеризуют способность тел притягивать друг друга. Масса, являющаяся мерой тяготения, называется гравитационной.
Опытным путем установлено, что гравитационная масса равна инертной (впервые доказал И. Ньютон).
Сила тяжести – сила, с которой Земля (или другое небесное тело) притягивает к себе различные тела.
Природа силы тяжести – гравитационная.
Примечание: 1. Сила тяжести приложена к телу.
2. Сила тяжести всегда направлена вертикально вниз (к центру Земли).
Из закона всемирного тяготения следует, что если тело находится на поверхности Земли (или другой планеты) или вблизи нее, то
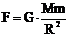, где
F – сила тяжести;
M – масса Земли (или другой планеты);
R – радиус Земли (или другой планеты);
m – масса тела;
G – гравитационная постоянная.
Для данного небесного тела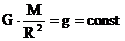 
.
Для Земли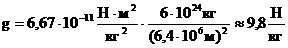 
(численно равна силе тяжести, действующей на тело массой 1 кг, находящееся на поверхности Земли или вблизи нее).
Тогда силу тяжести, действующую на тело массой m, можно определить по формуле:
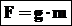, где
m – масса тела (должна быть выражена в кг!);
g – коэффициент пропорциональности.
Таким образом, сила тяжести прямо пропорциональна массе тела.
Выясним физический смысл g.
Из второго закона Ньютона следует, что любую силу, вне зависимости от природы. Можно вычислить как 
, где m* – инертная масса. С другой стороны 
, где m – гравитационная масса.
Т. е. 
. Исходя из равенства гравитационной и инертной масс, имеем, что a = g.
Следовательно, g – ускорение, которое сообщает сила тяжести всем телам (ускорение свободного падения)
Примечание: Ускорения свободного падения для различных небесных тел:
| Солнце | 274 м/с2 | Юпитер | 26 м/с2 |
| Меркурий | 3,7 м/с2 | Сатурн | 11 м/с2 |
| Венера | 8,9 м/с2 | Уран | 9 м/с2 |
| Земля | 9,8 м/с2 | Нептун | 12 м/с2 |
| Луна | 1,6 м/с2 | Плутон | 0,6 м/с2 |
| Марс | 3,7 м/с2 |
Если тело находится на высоте h над поверхностью Земли (или другой планеты), то силу тяжести рассчитывают по формуле:
Замечание: В общем случае коэффициент пропорциональности g зависит от массы небесного тела; его радиуса и от высоты над поверхностью небесного тела 
.
Задание: 1) Известно, что земной шар немного сплюснут у полюсов. Как изменится сила тяжести, действующая на тело, если: а) тело перенести с экватора на полюс; б) тело перенести в другое место земного шара, лежащее на той же широте?
2) Как изменится сила тяжести, действующая на тело, если его поднять с подножия горы на ее вершину?
3) Используя вышеприведенную таблицу или учебник (материал для дополнительного чтения п.3),запишите в тетради планеты, на которых сила тяжести: а) больше, чем на Земле; б) меньше, чем на Земле. С чем это связано?
Сила упругости.
Сила, возникающая в результате деформации тела и направленная в сторону, противоположную перемещению частиц тела при деформации, называется силой упругости.
Примечание: Сила упругости приложена к телу, вызвавшему деформацию.
Виды деформаций: растяжение, сжатие, изгиб, сдвиг, кручение. Все виды деформаций можно свести к деформациям растяжения и сдвига.
 |
РАСТЯЖЕНИЕ
СЖАТИЕ
 | |||
 | |||
СДВИГ КРУЧЕНИЕ
 | |||
 | |||
ИЗГИБ
Деформации, полностью исчезающие после прекращения действия силы, вызвавшей деформацию, называются упругими.
Если деформации, полностью не исчезают после прекращения действия силы, вызвавшей деформацию, то они называются пластическими.
Задание: Приведите примеры упругих и пластических деформаций.
Закон английского ученого РобертаГука (1635–1703): При упругих деформациях модуль силы упругости прямо пропорционален величине деформации.
, где
F – сила упругости;
x – величина деформации;
k – коэффициент пропорциональности, который называется жесткостью тела (или коэффициентом упругости).
Жесткость тела зависит от его размеров, формы и материала, из которого оно изготовлено.
Единица измерения жесткости тела в СИ: 1 ньютон на метр (
).
Примечание:
1. Сила упругости, возникающая в подвесе, называется силой натяжения подвеса.
Иногда обозначается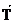 
.
2. Сила упругости, действующая на тело со стороны опоры и направленная перпендикулярно ее поверхности, называется силой реакции опоры.
Иногда обозначается 
.
Вес тела.
При взаимодействии тела с опорой (или подвесом) вследствие действия силы тяжести деформируется не только опора (или подвес), но и тело. В результате этого со стороны деформированного тела на опору (или подвес) действует сила упругости. Эта сила упругости называется весом тела.
Вес тела – это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес.
Обозначение: 
- вектор веса тела;
P – модуль веса тела.
Примечание:
1. Вес тела приложен к опоре (или подвесу).
2. Если тело и горизонтальная опора (вертикальный подвес) неподвижны или движутся равномерно и прямолинейно, то вес тела P по своему численному значению равен силе тяжести F: 
3. Невесомость – явление, при котором тело не действует на опору или подвес, то есть вес тела равен нулю.
Динамометр.
Динамометр – прибор для измерения силы.
Главная часть динамометра – пружина, растягивающаяся в пределах упругих деформаций. К пружине прикреплен указатель, скользящий вдоль шкалы, размеченной в единицах силы. Так как, согласно закону Гука, сила упругости прямо пропорциональна удлинению пружины, то шкала прибора равномерная.
Принцип действия пружинного динамометра основан на сравнении измеряемой силы с силой упругости пружины.
Задание: Объясните, как можно проградуировать пружину; как получить шкалу с ценой деления 0,1 Н.
