2018-01-08
2933
Минор 
матрицы A ― определитель квадратной матрицы порядка k (который называется также порядком этого минора), элементы которой стоят в матрице A на пересечении строк с номерами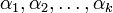 
и столбцов с номерами 
.
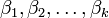Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то минор называется главным, а если отмечены первые k строк и первые k столбцов ― угловым или ведущим главным.
Дополнительный минор элемента матрицы n-го порядка есть определитель порядка (n-1), соответствующий той матрице, которая получается из матрицы путем вычеркивания i-ой строки и j-го столбца.
Базисным минором матрицы называется любой её ненулевой минор максимального порядка. Для того чтобы минор был базисным, необходимо и достаточно, чтобы все окаймляющие его миноры (то есть содержащие его миноры на единицу большего порядка) были равны нулю. Система строк (столбцов) матрицы, связанных с базисным минором, является максимальной линейно независимой подсистемой системы всех строк (столбцов) матрицы.
|
|
|
Алгебраическим дополнением элемента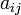 
матрицы 
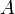называется число
,
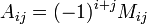где 
— дополнительный минор, определитель матрицы, получающейся из исходной матрицы 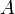путем вычёркивания i -й строки и j -го столбца.
Определителем n-го порядка (определителем квадратной матрицы n-го порядка n), n>1, называется число, равное
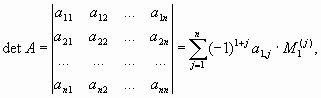
где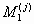 
— определитель квадратной матрицы полученной из матрицы A вычеркиванием превой строки и j-го столбца.
Для определителей 2 -го и 3- го порядка легко получить простые выражения через элементы матрицы.
Свойства определителей
Для определителей справедливы следующие утверждения, называемые свойствами определителей.
Определитель не изменяется при транспонировании: det A T=det A.
Если строка (столбец) матрицы A равна линейной комбинации соответственных строк (столбцов) матриц A и B, а остальные строки (столбцы) этих матриц совпадают, то ее определитель равен линейной комбинации определителей матриц A и B:
Ai = a·Bi + b·Ci, det A= a· det B + b· det C,
A(j) = a·B(j) + b·C(j), det A= a· det B + b· det C.
При перестановке любых двух строк (столбцов), определитель меняет знак.
Если в определителе есть две одинаковые строки (два одинаковых столбца), то он равен нулю.
Если в определителе есть две пропорциональные строки (два пропорциональные столбца), то он равен нулю.
Определитель не изменится, если к элементам любой его строки (столбца) прибавить элементы любой другой строки (столбца), умноженные на одно и то же число.
Определитель, содержащий нулевую строку (нулевой столбец), равен нулю.
Сумма произведений элементов любой строки (столбца) на алгебраические дополнения другой строки (другого столбца) равна нулю.
|
|
|
Определитель произведения матриц равен произведению определителей сомножителей.
Перечисленные свойства позволяют упростить вычисление определителя.
Пример.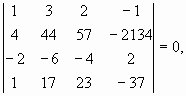 
поскольку 1-я и 3-я строки пропорциональны.
