Розв’язання інтегральних рівнянь
Інтегральним рівнянням називають рівняння відносно невідомої функції, яка знаходиться під знаком інтеграла.
Відомі закони збереження маси, імпульсу, енергії у своїй формалізованій постановці приводять до інтегральних рівнянь.
У загальному випадку інтегральне рівняння має такий вигляд:
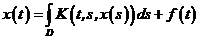 (7.1),
(7.1),
де 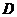 - деяка область
- деяка область 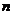 - вимірного простору;
- вимірного простору; 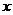 - невідома, а
- невідома, а 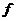 - відома векторні функції;
- відома векторні функції; 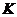 - у загальному випадку невідома відносно
- у загальному випадку невідома відносно 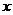 функція.
функція.
Будемо розглядати лише скалярні рівняння, тобто такі, в яких шуканою невідомою є скалярна функція однієї змінної, а область інтегрування 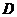 - відрізок
- відрізок 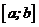 . Крім того будемо вважати, що підінтегральна функція
. Крім того будемо вважати, що підінтегральна функція 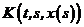 у (7.1) має наступний вигляд:
у (7.1) має наступний вигляд:
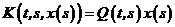 . (7.2)
. (7.2)
Інтегральні рівняння з підінтегральною функцією (7.2) називають лінійними інтегральними рівняннями.
В залежності від того чи постійні обидві межі інтегрування, чи одна із них може бути змінною, розрізняють лінійні інтегральні рівняння другого роду Фредгольма –
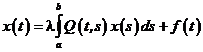 (7.3)
(7.3)
і Вольтеррі
|
|
|
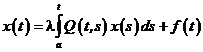 , (7.4)
, (7.4)
У рівняннях (7.3) і (7.4) задана і шукана функції 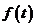
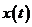 залежать від змінної
залежать від змінної 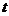 , область визначення якої відрізок
, область визначення якої відрізок 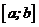 . Функція двох змінних
. Функція двох змінних 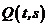 , яка називається ядром інтегрального рівняння, визначена на множині точок квадрата
, яка називається ядром інтегрального рівняння, визначена на множині точок квадрата 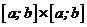 у випадку рівняння (7.3) (рис. 7.1,а) і трикутника
у випадку рівняння (7.3) (рис. 7.1,а) і трикутника 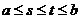 , якщо маємо рівняння Вольтеррі (рис. 7.1,б).
, якщо маємо рівняння Вольтеррі (рис. 7.1,б).
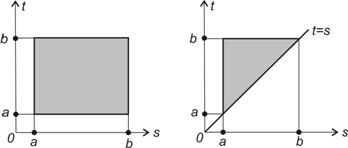
а) б)
Рисунок 7.1 Області визначення ядер 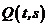 інтегральних рівнянь
інтегральних рівнянь
 2018-01-08
2018-01-08 274
274







