Наявність параметру  у рівнянь (7.3) і (7.4) надає цим рівнянням більш загальний вигляд і дає змогу виявити існування їх розв’язків при тих чи інших значенням
у рівнянь (7.3) і (7.4) надає цим рівнянням більш загальний вигляд і дає змогу виявити існування їх розв’язків при тих чи інших значенням  . Якщо допустити, що
. Якщо допустити, що  , то розв’язків рівнянь (7.3) і (7.4) може і не бути.
, то розв’язків рівнянь (7.3) і (7.4) може і не бути.
Нехай для обчислення визначеного інтегралу використовується деяка квадратурна формула
 ,
,
з 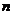 вузлами і з відповідними їм ваговими коефіцієнтами
вузлами і з відповідними їм ваговими коефіцієнтами  . Тоді отримаємо наближене подання розв’язку рівняння (7.3) через
. Тоді отримаємо наближене подання розв’язку рівняння (7.3) через 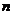 його значень
його значень  ,
,  , …,
, …, 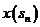
 , (7.5)
, (7.5)
де значення  ,
, 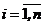 , співпадають з вузлами
, співпадають з вузлами  ,
,  .
.
Введемо такі позначення 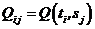 ,
, 
 і
і 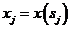 . Тоді, змінюючи
. Тоді, змінюючи  від 1 до
від 1 до 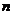 в (7.5), отримуємо систему лінійних алгебраїчних рівнянь
в (7.5), отримуємо систему лінійних алгебраїчних рівнянь
 ,
, 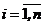 , (7.6)
, (7.6)
де  ,
,  ,
,  ;
;  ,
,  ,
, 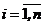 .
.
Систему рівнянь (7.6) можна розв’язати за допомогою процедури SystemEqualizationAgebra. Результатом такого розв’язку будуть значення  ,
,  , …,
, …,  , які утворюють каркас наближеного розв’язку інтегрального рівняння на сітці
, які утворюють каркас наближеного розв’язку інтегрального рівняння на сітці  ,
, 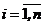 .
.
При фіксованих значеннях  і
і  системи рівнянь (7.6) зміною параметра
системи рівнянь (7.6) зміною параметра  (зменшення його модуля) можна покращити обумовленість[1] матриці коефіцієнтів
(зменшення його модуля) можна покращити обумовленість[1] матриці коефіцієнтів 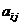 .
.
Для визначення параметрів  можна використати методи числового обчислення визначених інтегралів, наприклад метод трапецій чи метод Сімпсона.
можна використати методи числового обчислення визначених інтегралів, наприклад метод трапецій чи метод Сімпсона.
Використання метода трапецій приводить до такої складеної формули:
 ,
,
де  ;
;  - кількість під інтервалів, на які розбитий інтервал
- кількість під інтервалів, на які розбитий інтервал 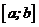 .
.
Таким чином,  ,
,  ,
,  , де
, де  .
.
У випадку використання формули Сімпсона будемо мати

 ,
,
де 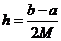 ;
;  ;
;  - кількість підінтервалів, на які розбитий інтервал
- кількість підінтервалів, на які розбитий інтервал 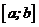 .
.
Із останнього співвідношення випливає, що  ,
,  ,
,  ,
, 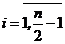 .
.
Точність числового розв’язку інтегрального рівняння квадратурним методом залежить від ряду взаємозв’язаних факторів: застосованої квадратурної формули, кількістю вузлів, які використовуються, властивостей функцій, що входять до інтегрального рівняння.
Параметр  у лінійних інтегральних рівняннях Вольтеррі не має ніякого смислового значення (на відміну від рівнянь Фредгольма). Тому, поклавши у (7.4)
у лінійних інтегральних рівняннях Вольтеррі не має ніякого смислового значення (на відміну від рівнянь Фредгольма). Тому, поклавши у (7.4)  , приходимо до рівняння
, приходимо до рівняння
 , (7.7)
, (7.7)
яке будемо розв’язувати числовим методом.
Позначимо  . Тоді можемо записати, що
. Тоді можемо записати, що

Рівняння (7.7) замінимо наближеним його аналогом
 ,
, 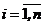 . (7.8)
. (7.8)
Змінюючи  від
від 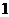 до
до 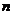 та, враховуючи прийняті раніше позначення, отримуємо систему лінійних алгебраїчних рівнянь
та, враховуючи прийняті раніше позначення, отримуємо систему лінійних алгебраїчних рівнянь
 ,
,
 , (7.9)
, (7.9)
…………………,
 ,
,
де  ,
,  ,
,  ;
;  ,
,  ,
, 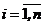 , із якої просто отримати шукані значення
, із якої просто отримати шукані значення  ,
,  , …,
, …,  .
.
Конкретне значення величини  ,
, 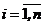 визначається квадратурною формулою для заміни визначених інтегралів у рівнянні (7.7) кінцевими сумами (7.8). Як приклад, розглянемо квадратурну формулу трапецій. У цьому випадку при
визначається квадратурною формулою для заміни визначених інтегралів у рівнянні (7.7) кінцевими сумами (7.8). Як приклад, розглянемо квадратурну формулу трапецій. У цьому випадку при 
 і
і  . Якщо
. Якщо  , то
, то  і
і
 ,
,
де  . З врахуванням (7.8) матимемо
. З врахуванням (7.8) матимемо
 .
.
Нехай  . Тоді
. Тоді  і відповідно
і відповідно
 .
.
Отриманий результат дає можливість записати
 .
.
Таким чином, для першого рівняння системи (7.9)  ; для другого рівняння -
; для другого рівняння -  ; для третього рівняння -
; для третього рівняння -  ,
, 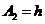 і т. д.
і т. д.
У загальному випадку будемо мати систему рівнянь (7.9), у якій  ,
,  ,
,  ,
,  ,
,  ,
,  , …,
, …, 
 , …,
, …,  .
.
Система лінійних алгебраїчних рівнянь (7.9) є верхньою трикутною і її розв’язок легко знайти, визначивши  з першого рівняння. Потім, підставивши знайдене значення
з першого рівняння. Потім, підставивши знайдене значення  у друге рівняння, знову матимемо рівняння з одним невідомим, яке розв’яжемо відносно
у друге рівняння, знову матимемо рівняння з одним невідомим, яке розв’яжемо відносно  і т. д. У загальному випадку приходимо до такої формули:
і т. д. У загальному випадку приходимо до такої формули:
 , (7.10)
, (7.10)
яка дає змогу визначити каркасний наближений розв’язок інтегрального рівняння на сітці  ,
, 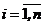 .
.
Приклад 7.1. Знайти каркасний наближений розв’язок інтегрального рівняння Вольтеррі
 . (7.11)
. (7.11)
У нашому випадку  ,
,  . До рівняння (7.11) застосуємо квадратурну формулу трапецій з постійним кроком
. До рівняння (7.11) застосуємо квадратурну формулу трапецій з постійним кроком  . Задамо число вузлів
. Задамо число вузлів 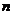 і кінцевий час
і кінцевий час  . Тоді
. Тоді 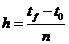 , де
, де  - початковий час. На рис. 7.2 показана сітка для числового розв’язку інтегрального рівняння Вольтеррі.
- початковий час. На рис. 7.2 показана сітка для числового розв’язку інтегрального рівняння Вольтеррі.
Для подальших обчислень створимо процедуру, яку назвемо EqualizationVolterri
EqualizationVolterri
 Задати числові значення n, t0, tf та обчислити крок h
Задати числові значення n, t0, tf та обчислити крок h
 Сформувати вузли ti si i=1, 2, …, n
Сформувати вузли ti si i=1, 2, …, n
 Обчислення коефіцієнтів aij
Обчислення коефіцієнтів aij
1 for i=1 to n
2 if i=1
3 then a(i,i)=1
4 end if
5 for j=1 to i
6 Обчислити Q=Qij
7 if j=i
8 then a(i,j)=1-h*Q/2
9 elseif j=1
10 then a(i,j)=-h*Q/2
11 else
12 a(i,j)=-h*Q
13 end if
14 end for
15 end for
 Обчислити bi=f(ti), i=1, 2, …, n
Обчислити bi=f(ti), i=1, 2, …, n
 Розв’язок верхньої трикутної системи лінійних алгебраїчних рівнянь
Розв’язок верхньої трикутної системи лінійних алгебраїчних рівнянь
16 x(1)=f(1)
17 for i=2 to n
18 s=0
19 for j=1 to i-1
20 s=s+a(i,j)*x(j)
21 end
22 x(i)=(b(i)-s)/a(i,i)
23 end for
 Побудувати графік у координатах t, x
Побудувати графік у координатах t, x

Рисунок 7.2 – Сітка числового розв’язку інтегрального рівняння Вольтеррі
Процедуру EqualizationVolterri реалізовано при наступних значеннях параметрів:  ,
,  ,
,  . На рис. 7.3 показаний графік (суцільна лінія) каркасного розв’язку
. На рис. 7.3 показаний графік (суцільна лінія) каркасного розв’язку  ,
,  інтегрального рівняння Вольтеррі (7.11). Той же рисунок вміщує графік (пунктирна лінія) точного розв’язку рівняння (7.11) -
інтегрального рівняння Вольтеррі (7.11). Той же рисунок вміщує графік (пунктирна лінія) точного розв’язку рівняння (7.11) -  .
.

Рисунок 7.3 – Графіки функцій 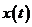 - розв’язку інтегрального рівняння Вольтеррі (7.11)
- розв’язку інтегрального рівняння Вольтеррі (7.11)
Із рисунка видно, що по мірі віддалення  від свого початкового значення
від свого початкового значення  похибка обчислення
похибка обчислення  зростає. Підвищити точність розв’язку задачі (7.11) можна збільшити, якщо використовувати точніші квадратурні формули для обчислення визначених інтегралів.
зростає. Підвищити точність розв’язку задачі (7.11) можна збільшити, якщо використовувати точніші квадратурні формули для обчислення визначених інтегралів.
Контрольні питання та завдання
1. Дайте визначення інтегрального рівняння.
2. Яку назву мають інтегральні рівняння з постійною і змінною верхніми межами інтегрування?
3. Як знайти каркас наближеного розв’язку інтегрального рівняння?
4. Як підвищити точність розв’язку інтегрального рівняння при використанні числових методів?
5. Задано рівняння 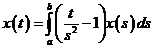 . Знайти його наближений розв’язок, використавши формулу трапецій, якщо
. Знайти його наближений розв’язок, використавши формулу трапецій, якщо  ,
,  . Порівняйте отриманий результат з точним його розв’язком
. Порівняйте отриманий результат з точним його розв’язком  .
.
[1] Числом обумовленості матриці розміром називають величину, де через позначено норму відповідної матриці. Норма матриці це деяка скалярна величина, яка може бути визначена одним із трьох способів:
1. - максимум суми модулів елементів матриці у стовпці.
2. - квадратний корінь максимального власного значення симетричної матриці.
3. - максимум суми модулів елементів матриці у рядку.
При великих точний розв’язок системи лінійних рівнянь може суттєво змінюватись навіть при малих змінах вхідних даних. Матриця з великим називається погано обумовленою матрицею.
 2018-01-08
2018-01-08 422
422







