Методи розв’язку систем нелінійних рівнянь

Допустимо, що необхідно розв’язати систему нелінійних рівнянь.

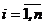, (5.17)

де 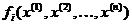, відомі дійсні нелінійні функції своїх змінних , які є також дійсними.

Рівняння (5.17) подано у матрично векторній формі:

, (5.18)

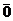де = - - вимірна вектор функція; - - вимірний вектор змінних - - вимірний нуль-вектор.

Допустимо, що рівняння (5.18) можна записати у такому вигляді:

, (5.19)

де - деяка вектор-функція.

На основі (5.19) можна отримати формальну рекурентну рівність

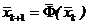, (5.20)

яка визначає метод простих ітерацій (МПІ).

За певних умов* (див. с. 283-285) ітераційний процес буде збіжним, тобто

, (5.21)

де -вектор, який є розв’язком рівняння (5.18).

Щоб метод простих ітерацій застосувати до розв’язку будь-якого нелінійного рівняння, яке приведено до (5.18), необхідно здійснити наступне формальне перетворення. Помножимо рівняння (5.18) на деяку невласну 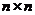- матрицю , взяту зі знаком мінус: .

Тепер до лівої і правої частини додамо вектор невідомих 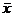. В результаті отримаємо

. (5.22)

Проблема полягає в підборі елементів матриці таких, щоб ітераційний процес

(5.23)

був збіжним, тобто виконувалася умова (5.21). У залежності від вибору елементів матриці отримаємо різні ітераційні процедури пошуку коренів системи нелінійних рівнянь (5.17)

Метод Ньютона. Якщо

де 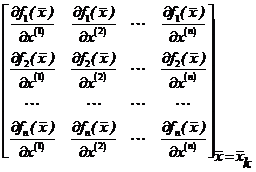- матриця Якобі, то

. (5.24)

Формула (5.24) є прямим аналогом метода Ньютона для скалярної функції , де похідна замінена на матрицю обернену до матриці Якобі.

Модифікований метод Ньютона. Метод Ньютона вимагає на кожній ітерації знаходження оберненої матриці , що значно збільшує обчислювальні затрати. Ці затрати можна зменшити, якщо матрицю обчислювати лише у початковій точці . У результаті отримаємо модифікований метод Ньютона

. (5.25)

З іншої сторони реалізація модифікованого методу Ньютона може привести до збільшення кількості ітерацій для досягнення заданої точності розв’язку задачі (5.18).

Дискретний метод Ньютона. На базі метода Ньютона можна отримати близький до нього ітераційний процес, який не вимагає обчислення похідних. Досягти цього можна, замінивши в матриці Якобі часткові похідні різницевим відношенням

,

де .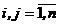

Тоді , де - матриця Якобі, в якій часткові похідні замінені кінцевими відношеннями, що приводить до дискретного методу Ньютона

. (5.26)

Якщо взяти , то отримаємо метод січних, який узагальнений на багатовимірну задачу (5.13).

 

Контрольні питання та завдання

 

1 Які методи застосовують для розв'язку нелінійних алгебраїчних рівнянь?

2 Як знайти інтервал на якому функція дорівнює нулю?

3 Чи означає умова , що рівняння =0 не має жодного кореня на інтервалі ?

4 Чи означає умова , що рівняння =0 має єдиний корінь на інтервалі ?

5 Які переваги і недоліки методу дихотомії над іншими числовими методами розв'язку рівняння =0?

6 У якому випадку метод хорд збігається швидше у порівнянні з методом дихотомії?

7 За рахунок чого забезпечується вища збіжність методу Ньютона-Рафсона у порівнянні з методами дихотомії і хорд?

8. Яким чином оцінити похибку розв'язку рівняння =0 методом Ньютона-Рафсона?

9 Чим пояснити появу модифікацій методу Ньютона-Рафсона?

10 Використовуючи програми процедуру MethodChords знайти локальний корінь рівняння .

11 Охарактеризуйте методи розв'язку систем нелінійних алгебраїчних рівнянь.

 

 

* Вержбицкий В. М. Основы численных методов. Учебник. – М.: Высш. шк., 2002. – 840 с.