Розв’язок нелінійних рівнянь

Задачі нелінійної алгебри

Будемо розглядати задачу знаходження коренів рівняння

=0, (5.1)

де - алгебраїчна або трансцендентна функція.

Розв’язати рівняння (5.1) означає знайти такі значення аргументу , при яких виконується рівність

=0.

У загальному випадку аналітичним способом рівняння (5.1) не розв’язується і тоді звертаються до числових методів, які дають можливість лише наближено обчислювати корені рівняння (5.1).Нехай точне значення j -го кореня, а - його наближення. Тоді під близькістю наближеного значення 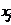до його істинного розуміють виконання нерівності

= <

при малих >0. Іноді важливо контролювати не абсолютну похибку _, а відносну

=

особливо, коли величина близька до нуля.

Нелінійна функція у своїй області визначення може мати кінцеве чи нескінченне число коренів, або не мати їх взагалі.

Переважна більшість числових методів знаходження коренів(нулів) функції вимагає знання інтервалів 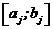, де знаходиться єдиний корінь. Для функцій загального вигляду немає універсальних способів знаходження інтервалів 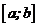. Найпростіший з них є спосіб побудови графіка (якщо це можливо) функції (рис.5.1).

 

Рисунок 5.1 – Знаходження інтервалів за допомогою графіка функції .

 

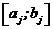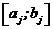Алгоритмічний спосіб (за допомогою ЕОМ) визначення інтервалів ґрунтується на порівнянні знаків функції на кінцях інтервалу . В тому випадку, коли

, (5.2)

то на інтервалі 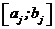функція принаймні один раз приймає значення нуль. Такий спосіб має один суттєвий недолік: він не дає відповіді на питання про кількість коренів на інтервалі .

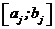У випадку виконання умови (5.2) їх може бути більше одного і їх кількість є непарне число (рис. 5.2, а);

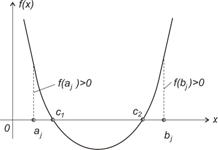
На рисунку 5.2,б показаний випадок, коли умова (5.2) не виконується, хоча відрізок вміщує два корені (кількість коренів парне число).

 

а)

б)

 

Рисунок 5.2 – Приклади непарної (а) і парної (б) кількості коренів функції на інтервалі .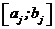

 

Для того, щоб умова (5.2), однозначно давала відповідь про єдиний корінь на інтервалі 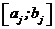необхідно і достатньо, щоб функція на цьому інтервалі була б неперервною і строго монотонною.

Для неперервних функцій властивість монотонності на інтервалі 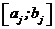означає, що похідна не змінює свого знаку на цьому інтервалі.

Знаходження інтервалу 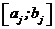, який вміщує єдиний нуль функції носить назву способу локалізації коренів.

Метод дихотомії. Вказаний спосіб локалізації коренів є основою розв'язку нелінійного рівняння (5.1) і носить назву методу дихотомії (бісекції).

Допустимо, що на відрізку 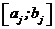функція неперервна і монотонна, крім того і мають протилежні знаки. Це означає, що інтервал 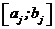вміщує єдиний корінь. Визначальною операцією у процесі поділу інтервалу наполовину є вибір середньої точки і аналіз трьох можливостей, які при цьому можуть виникнути:

i) якщо і мають різні знаки, то нуль належить інтервалу ;

ii) якщо і мають різні знаки, то нуль належить інтервалу ;

iii) якщо =0, то .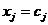

Випадки і) та іі) ілюструє рис. 5.3.

 

 

а) укорочення інтервалу зліва;

 

 

б) укорочення інтервалу справа

 

Рисунок 5.3 – Розв’язок рівняння =0 методом дихотомії:

 

Подальші обчислення відбуваються за таким алгоритмом:

К1. Ділимо відрізок 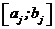наполовину і знаходимо середню точку:

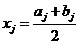
К2. Якщо =0; кінець обчислень.

К3. Якщо <0, то і перейти до К1.

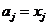К6. Якщо ) <0, то і перейти до К1.

Умова на другому кроці (К2), як правило, не виконується, оскільки, ітераційний процес дає можливість знайти лише наближене значення кореня. Тому її слід замінити іншою умовою , де >0 – досить мати число, яке визначає точність розв’язку задачі.

Оскільки на кожному кроці ітерації вихідний відрізок ділиться наполовину, то він породжує таку послідовність точок, що

, (5.3)

Це означає, що послідовність значень при k .

Наведена нижче процедура MethodDichotomy, яка подана у псевдокоді, розв’язує нелінійне рівняння 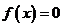методом дихотомії із заданою точністю .

 

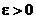MethodDichotomy^*

 

Вхід процедури

Функція f(x)

a та b – початок і кінець інтервалу [a;b], який вміщує корінь рівняння f(x)=0

epsilon – точність розв’язку задачі f(x)=0

N – число ітерацій

Вихід процедури

с – корінь рівняння f(x)=0

Yc – значення функції f(x) при х=с

Функці f(x) задається процедурою fun_Solve

Побудова графіка функції f(x)

Задати початковий і кінцевий інтервали x0 s xk, на якому функція f(x) унімодальна, а також крок delta

1 k=0

2 for x=x0 step delta to xk

3 k=k+1

4 X(k)=x

5 Y(k)=fun_Solve(x)

6 end for

8 plot(X,Y)

Із графіка функції f(x) знаходимо інтервал локального нуля [a;b]

9 Ya=fun_Solve(a)

10 Yb=fun_Solve(b)

11 if Ya*Yb>0

12 then error(‘Неправильний інтервал локального нуля’)

13 end if

Обчислення кількості ітерацій

14 N=1+round((ln((b-a)/epsilon))/ln(2))

Реалізація процесу дихотомії

15 for k=1 to N

16 c=(a+b)/2

17 Yc=fun_Solve©

18 if Yc=0

19 then a=c

20 b=c

21 end if

22 if Yb*Yc>0

23 then b=c

24 Yb=Yc

25 else a=c

26 Ya=Yc

27 end if

28 if b-a<epsilon

29 then вихід із циклу

30 end if

31 end for

32 c=(a+b)/2

33 Yc=fun_Solve(c)

 

Для знаходження інтервалу 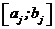, який вміщує локальний корінь функції процедура MethodDichotomy будує графік (рядки 1 – 8), із якого знаходимо значення і .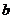

Якщо задана точність розв'язку задачі =0 - 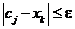, то із (5.3) визначимо максимальну кількість ітерацій N, яка необхідна для досягнення заданої точності .

N = max: k = ,

де [...]- ціла частина числа.

 

Метод хорд. Метод дихотомії має невелику збіжність. Збіжність алгоритму розв’язку задачі =0 можна збільшити, якщо відрізок 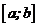ділити точкою на частини не навпіл, а пропорційно величинам ординат та функції . Як і раніше допускаємо, що і мають протилежні знаки. Знайдемо точку , в якій хорда L, що з’єднує точки i пересікає вісь (рис.5. 4)

а)

б)

Рисунок 5.4 – Процес розв’язку задачі =0 методом дихотомії.

 

Знайдемо значення . Для цього спочатку визначимо кут нахилу прямої L до осі абсцис з використанням точок i (рис 5.5).

m = tg a= . (5.5)

Цей же кут знайдемо, використавши точки і

m = (5.6)

 

Прирівнявши між собою праві частини рівнянь (5.5) і (5.6), знаходимо

.

Тут, як і в методі дихотомії існують три можливості:

i) якщо i мають різні знаки, то корінь рівняння =0 належить інтервалу ;

ii) якщо i мають різні знаки, то (рис.5.5,б);

iii) якщо =0, то коренем функції є значення .

Остання формула разом з і) та іі) використовується для побудови ітераційної процедури

.

Метод хорд збігається значно швидше, ніж метод дихотомії в тому випадку, коли близька до лінійної функції. Але у загальному випадку може статися, що метод хорд буде програвати у швидкості методу дихотомії тоді, коли значно відрізняється від прямої лінії.

 

Рисунок 5.5 – Наближення до кореня функції за методом хорд.

 

Наступна процедура MethodChords знаходить розв’язок задачі 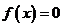методом хорд.

 

MethodChords^*

Вхід процедури

Функція f(x)

a та b – початок і кінець інтервалу [a;b], який вміщує корінь рівняння f(x)=0

epsilon – точність розв’язку задачі f(x)=0

eps – граничне відхилення f(x) у нулі

N – число ітерацій

Вихід процедури

с – корінь рівняння f(x)=0

Yc – значення функції f(x) при х=с

Функці f(x) задається процедурою fun_Solve

1 Побудувати графік функції f(x) і знайти інтервал [a; b], який вміщує локальний корінь

2 Ya=fun_Solve(a)

3 Yb=fun_Solve(b)

4 if Ya*Yb>0

5 then error(‘Неправильний інтервал локального нуля’)

6 end for

Реалізація процедури методу хорд

7 for k=1 to N

8 Dx=Yb*(b-a)/(Yb-Ta)

9 c=b-Dx

10 ac=c-a

11 Yc= fun_Solve(c)

12 if Yc=0

13 then вихід із циклу

14 end if

15 if Yb*Yc>0

16 then b=c

17 Yb=Yc

18 else

19 a=c

20 Ya=Yc

21 end if

22 Dx=Min(abs(Dx),ac)

23 if abs(Dx)<epsilon

24 then вихід із циклу

25 end if

26 if abs(Dx)<eps

27 then вихід із циклу

28 end if

29 end for

Корінь рівняння f(x)=0

30 c=(a+b)/2

31 Yc= fun_Solve(c)

 

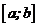Метод Ньютона-Рафсона. Цей метод має вищу збіжність у порівнянні з методами дихотомії і хорд. Будемо вважати, що функція f(x) має першу та другу похідні і нехай – інтервал локального кореня. На інтервалі 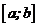функцію f(x) розкладемо у ряд Тейлора, обмежившись лише лінійним членом.

, (5.7)

де ;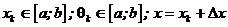

- залишковий член ряду;

- приріст аргументу.

Оскільки , то рівняння (5.7) набуде такого вигляду:

(5.8).

Рівняння (5.8) справедливе для будь-якого х із інтервалу 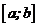.Справедливо і для

.

Але . Тому

. (5.9)

У тому випадку, коли близьке до , тоді у (5.9) можна знехтувати квадратним членом, але у такому випадку будемо мати не корінь с, а деяку іншу точку . Отже,

. (5.10)

Із останнього рівняння знаходимо вираз

, (5.11)

який і визначає ітераційний процес Ньютона-Рафсона.

Із рівняння (5.10) можна утворити деяку функцію шляхом заміни на

.

Це рівняння прямої лінії, яка є дотичною до функції у точці . Звідси випливає і геометричний зміст методу Ньютона-Рафсона: наближення до кореня функції здійснюється за абсцисами точок пересічень дотичних до , які проведені у точках попередніх наближень (рис 5.6).

 

 

Рисунок 5.6 – Наближення до кореня функції методом Ньютона-Рафсона

 

Геометричне тлумачення методу Ньютона-Рафсона дало йому другу назву – метод дотичних.

У тому випадку, коли перша похідна обмежена знизу , а друга похідна - , можна знайти апостеріорну оцінку похибки методу Ньютона-Рафсона

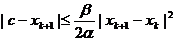, де с, . (5.12)

При реалізації ітераційної процедури (5.11) виникає питання про вибір початкової точки , яка за вимогою методу, повинна бути близькою до кореня с функції 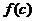. У тому випадку, коли похідні і на інтервалі 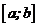мають постійні знаки, 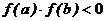і стартова точка 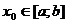вибрана так, що ,то починаючи з неї послідовність , яка визначена процедурою (5.11), монотонно збігається до кореня с функції .

Метод січних. У методі Ньютона-Рафсона для реалізації ітераційної процедури необхідно обчислювати дві функції і на кожному -му кроці. Для простих функцій обчислення не викликає особливих труднощів, У тих випадках, коли мають форму інтегралів, сум і т.д. бажано мати метод, який збігається майже так швидко, як і метод Ньютона-Рафсона, але не вимагає інформації про значення похідної .

У методі січних похідна обчислюється тільки один раз в точці . У подальшому нахил прямої L (рис 5.8) до вісі абсцис залишається незмінним, тобто

. (5.13)

 

Рисунок 5.7 – Наближення до кореня с методом січних

 

Ітераційна процедура (5.13) втрачає високу швидкість збіжності і замість квадратичної (5.12) має лише швидкість збіжності геометричної прогресії. Зменшення швидкості збіжності процедури (5.13) пояснюється тим, що процес не реагує на зміну нахилу кривої при наближенні до с. Збільшити швидкість збіжності можна, якщо на кожному кроці процедури (5.11) похідну замінити її наближенням

.

Оскільки , то

, (5.14)

Підставляючи (5.14) у (5.11) отримують процедуру

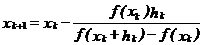, (5.15)

яку називають різницевим методом Ньютона.

Якщо у (5.15) покласти рівним: ,то отримаємо

. (5.16)

Ітераційна процедура (5.16) носить назву модифікованого методу січних. Цей метод на -ому кроці наближення дає похибку, яка обчислюється за такою формулою:

,

де , , .

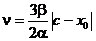Високий порядок швидкості збіжності ітераційної процедури (5.16) у поєднані з невеликими обчислювальними затратами виводять модифікований методом січних за ефективністю вирішення задачі на перше місце, що підтверджується як теоретичними, так і практичними висновками.