Схема исследования функции. Алгоритм решения показательных неравенств Алгоритм Образец решения 1

Алгоритм решения показательных неравенств

Алгоритм	Образец решения
1. Выбираем основание
2. Приводим обе части неравенства к одному основанию
3. Если a > 1,то функция возрастающая, значит, знакнеравенства сохраняем; Если 0 < a < 1,то функция убывающая, значит, знак неравенства меняем.	так как а = 2 > 1, то функция 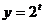возрастающая, значит,
4. Решаем полученное неравенство
5. Решение отмечаем на числовой оси
6. Ответ

 

 

 

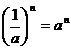
Преобразование графика функции y = f(x)

 

1.	f(x)+A	Параллельный перенос графика по оси у на А единиц: вверх, если А > 0, вниз, если А < 0.
2.	f(x-B)	Параллельный перенос графика вдоль оси х на В единиц: вправо, если В > 0, влево, если В < 0.   (подсказка: решить уравнение х - В = 0, где х = В, затем определять знак числа В и направление переноса)
3.	C ∙ f(x)	Умножение каждой ординаты у графика функции на число С
4.	f(D∙x)	Деление каждой абсциссы х   графика функции на число D
5.	- f(x)	«Зеркальное» отображение графика функции относительно оси х   (подсказка: смотри пункт 3)

 

 

Схема исследования функции

1. Область определения функции . Обозн.

 

2. Исследование функции на чётность и нечётность:

· если , то функция чётная

· если , то функция нечётная

· если оба условия не выполняются, то функция – ни чётная и ни нечётная

 

3. Определение точек пересечения с осью х:

 

4. Определение точек пересечения с осью y: ,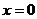

 

5. Промежутки возрастания и убывания функции:

· находим производную функции

· находим критические точки

· если на промежутке, то функция возрастает на этом промежутке

· если на промежутке, то функция убывает на этом промежутке

 

6. Точки экстремума: , .

 

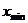7. Контрольные точки.

 

8. Построение графика функции .

 

 

Наибольшее и наименьшее значения функции y = f(x)

на отрезке [ а; в ]

 

1. Область определения функции . Обозн. .

 

2. Находим производную функции .

 

3. Находим критические точки .

 

4. Если , то находим , и .

 

5. Выбираем из полученных значений наибольшее и наименьшее.

 

6. Ответ: ; .

 

 

Уравнение касательной к графику функции y = f(x) в точке х₀

 

1. Запишите общий вид уравнения касательной .

 

2. Находим .

 

3. Находим .

 

4. Находим .

 

5. Подставляем в пункт 1 результаты 2 и 4пунктов.

Приводим к виду .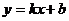

 

6. Ответ: 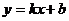- уравнение касательной к графику функции y = f(x) в точке х₀

 

 

Геометрический смысл производной функции y = f(x)

 

 

y = f(x)

 

 

 

 

 

--------------------------׀

¦

¦

¦

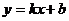
а ¦

¦

х₀