Закон Био — Савара- Лапласса. Магнитное поле, создаваемое круговым током, бесконечным прямолинейным проводником с током

Выясним характер магнитного поля, создаваемого произвольным тонким проводом, по которому течет ток. Рассмотрим малый элемент провода длины dl. В этом элементе содержится nS dl носителей тока (n — число носителей в единице объема, S — площадь попе- речного сечения провода в том месте, где взят элемент dl). В точке положение которой относительно элемента dl определяется радиусом-вектором г (отдельный носитель тока е создает поле с индукцией .

Здесь v — скорость хаотического движения, а u — скорость упорядоченного движения носителя.

Значение магнитной индукции, усредненное по носителям тока, заключенным в элементе dl, равно =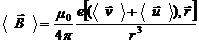

(<v>=0). Умножив это выражение на число носителей в элементе провода (равное nS dl), получим вклад в поле, вносимый элементом dl: (мы внесли скалярные множители n и е

под знак векторного произведения). Приняв во внимание, что ne<u>=j, можно получить .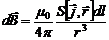

Введем вектор , направленный по оси элемента тока длиной в сторону, в которую течет ток. Модуль этого вектора равен dl. Поскольку направления векторов j и dl совпадают, имеет место равенство

Произведя такую замену в формуле для dB, получим

Учли, что произведение Sj дает силу тока I в проводе, придем к окончательному выражению, определяющему магнитную индукцию поля, создаваемого элементом тока длины dl:

Мы вывели формулу. В действительности последняя формула была установлена экспериментально.

Био и Савар провели в 1820 г. исследование магнитных полей, текущих по тонким проводам различной формы. Лаплас проанализировал экспериментальные данные, полученные Био и Саваром, и нашел, что магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельным, элементарными участками токов.

Для магнитной индукции поля, создаваемого элементом тока длины dl, Лаплас получил формулу , которая носит название закона Био — Савара — Лапласа или более кратко закона Б и о — Савара.

 

Из рис. 42.1видно, что вектор dB направлен перпендикулярно к плоскости, проходящей через d l и точку, в которой вычисляется поле, причем так, что вращение вокруг d l в направлении d B связано с d l правилом правого винта. Модуль dB определяется выражением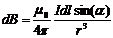

где α— угол между векторами dl и г. Применим формулу закона Б-С-Л для вычисления поля прямого тока, т. е. поля, создаваемого током, текущим по тонкому прямому проводу бесконечной длины (рис. 42.2 Сав 122). Все векторы dB в данной точке имеют одинаковое направление (в нашем случае за чертеж).

Поэтому сложение векторов dB можно заменить сложением их модулей. Точка, для которой мы вычисляем магнитную индукцию, находится на расстоянии b от провода.

Из рис. 42.2 видно, что Подставим эти значения в формулу

Угол α для всех элементов бесконечного прямого тока изменяется от 0 до π. Следовательно, магнитная индукция поля прямого тока определяется формулой

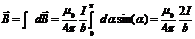Линии магнитной индукции поля прямого тока представляют собой систему охватывающих провод концентрических окружностей

(рис. 42.3 Сав 122).

16. Магнитное поле кругового контура с током

Рассмотрим поле, создаваемое током, текущим по тонкому проводу, имеющему форму окружности радиуса R (круговой ток). Определим магнитную индукцию в центре кругового тока (рис. 47.1 Сав. 138).

Каждый элемент тока создает в центре индукцию, направленную вдоль положительной нормали к контуру. Поэтому векторное сложение d В сводится к сложению их модулей.

По формуле 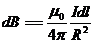(α=π/2). Проинтегрируем это выражение по всему контуру:

Выражение в скобках равно модулю дипольного магнитного момента p_m. Следовательно, магнитная индукция в центре кругового тока имеет величину

Из рис. 47.1 видно, что направление вектора В совпадает с направлением положительной нормали к контуру, т. е. с направлением вектора p_m. Поэтому последнюю формулу можно написать в векторном виде: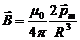

Теперь найдем В на оси кругового тока на расстоянии г от центра контура (рис. 47.2 Сав.138). Векторы d B перпендикулярны к плоскостям, проходящим через соответствующий элемент d l и точку, в которой мы ищем поле. Следовательно, они образуют симметричный конический веер (рис. 47.2, б, Cfd 138). Из соображений симметрии можно заключить, что результирующий вектор В направлен вдоль оси контура.

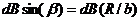Каждый из составляющих векторов d B вносит в результирующие вектор вклад , равный по модулю . Угол α между d l и b прямой, поэтому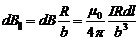

Проинтегрировав по всему контуру и заменив b на получим

.Эта формула определяет величину магнитной индукции на оси кругового тока.

 

Приняв во внимание, что векторы В и p_m имеют одинаковое направление, можно написать последнюю формулу в векторном виде: .

Это выражение не зависит от знака г. Следовательно, в точках оси, симметричных относительно центра тока, В имеет одинаковую величину и направление. При г=0 формула переходит, как и должно быть , в формулу для магнитной индукции в центре кругового тока. На больших расстояниях от контура в знаменателе можно пренебречь R² по сравнению с г². Тогда формула принимает вид .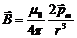

 

17. Теорема о циркуляции вектора магнитной индукции, ее применение для расчета маг нитного поля в бесконечном соленоиде.

Отсутствие в природе магнитных зарядов приводит к тому, что линии вектора В не имеют ни начала, ни конца. Поэтому поток вектора В через замкнутую поверхность должен быть равен нулю. Таким образом, для любого магнитного поля и произвольной замкнутой поверхности S имеет место условие . Эта формула выражает теорему Гаусса для вектора В: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.

 

Заменив поверхностный интеграл объемным, получим, что .

Условие, к которому мы пришли, должно выполняться для любого произвольно выбранного объема V. Это возможно лишь в том случае, если подынтегральная функция в каждой точке поля равна нулю. Таким образом, магнитное поле обладает тем свойством, что

его дивергенция всюду равна нулю: .

Найдем циркуляции вектора В. По определению циркуляция равна интегралу .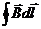

Проще всего вычислить этот интеграл в случае поля прямого тока. Пусть замкнутый контур лежит в плоскости, перпендикулярной к току (рис.; ток перпендикулярен к плоскости чертежа и направлен за чертеж). В каждой точке контура вектор В направлен по касательной к окружности, проходящей через эту точку. Заменим в выражении для циркуляции В d l через В dl_B (dl_B — проекция элемента контура на направление вектора В).

 

Из рисунка видно, что dl_B равно b dα, где b — расстояние от провода с током до d l, dα — угол, на который поворачивается радиальная прямая при перемещении вдоль контура на отрезок d l. Таким образом, для В, получим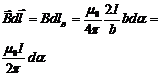

Окончательно будем иметь

При обходе по контуру, охватывающему ток, радиальная прямая все время поворачивается в одном направлении, поэтому .

Иначе обстоит дело, если ток не охватывается контуром (рис. 49.1,б). В этом случае при обходе по контуру радиальная прямая поворачивается сначала в одном направлении (участок 1—2), а затем в противоположном (участок 2—1), вследствие чего равен нулю. Учтя этот результат, можно написать , где под I следует подразумевать ток, охватываемый контуром. Если контур тока не охватывает, циркуляция вектора В равна нулю. Знак в выражении зависит от направления обхода по контуру (в этом же направлении отсчитывается угол α).

Если направление обхода образует с направлением тока правовинтовую систему, величина положительна, в противном случае — отрицательна. Знак можно учесть, полагая I алгебраической величиной, причем положительным нужно считать ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления будет отрицательным Поле соленоида

Соленоид представляет собой провод, навитый на круглый цилиндрический каркас. Линии В поля соленоида выглядят пример но так, как показано на рис. 50.1.

Внутри соленоида направление этих линий образует с направлением тока в витках правовинтовую систему. У реального соленоида имеется составляющая тока вдоль оси. Кроме того, линейная плотность тока j_лин (равная отношению силы тока dI к элементу длины соленоида dl) изменяется периодически при перемещении вдоль соленоида. Среднее значение этой плотности равно , где n— число витков соленоида, приходящееся на единицу его длины I — сила тока в соленоиде.

В соответствии со сказанным представим соленоид в виде бесконечного тонкостенного цилиндра (отсутствует осевая составляющая тока и, кроме того, линейная плотность тока j_лин постоянна по всей длине), обтекаемого током постоянной линейной плотности j_лин=nI.

Разобьем цилиндр на одинаковые круговые токи—«витки». Из.рис. видно, что каждая пара витков, расположенных симметрично относительно некоторой плоскости, перпендикулярной к оси соленоида, создает в любой точке этой плоскости магнитную индукцию, параллельную оси. Следовательно, и результирующее поле в любой точке внутри и вне бесконечного соленоида может иметь лишь направление, параллельное оси. Из рис. 50.1 вытекает, что направления поля внутри и вне конечного соленоида противоположны. При увеличении длины соленоида направления полей не изменяются и в пределе при противоположными. Для бесконечного соленоида, как и для конечного, направление поля внутри соленоида образует с направлением обтекания цилиндра током правовинтовую систему. Из параллельности вектора В оси вытекает, что поле как внутри, так и вне бесконечного соленоида должно быть однородным. Чтобы доказать это, возьмем внутри соленоида воображаемый прямоугольный контур 1—2—3—4 (рис. 50.3; участок 4—1 идет по оси соленоида). Обойдя контур по часовой стрелке, получим для циркуляции вектора В значение (B₂ –B₁)α. Контур не охватывает токов, поэтому циркуляция должна быть равна нулю.

Отсюда следует, что B₁=B₂. Располагая участок контура 2—3 на любом расстоянии от оси, мы каждый раз будем получать, что магнитная индукция В2 на этом расстоянии равна индукции B₁ на оси соленоида. Таким образом, однородность поля внутри соленоида доказана. Теперь обратимся к контуру 1'—2'—3'—4'. Мы изобразили векторы B`<sub>1</sub>и В`₂ штриховой линией, поскольку, поле вне бесконечного соленоида равно нулю. Контур 1'—2'—3'—4'не охватывает токов; поэтому циркуляция вектора В' по этому контуру, равная (B`<sub>1</sub>-В`₂)α, должна быть равна нулю.

Отсюда вытекает, что B `<sub>1</sub>= В `₂. Расстояния от оси соленоида до участков /' — 4' и 2' — 3' были взяты произвольно. Следовательно, значение В' на любом расстоянии от оси будет вне соленоида одно и то же. Таким образом, оказывается доказанной и однородность поля вне соленоида.

Циркуляция по контуру, изображенному на рис. 50.4 (Сав. 150), равна α(В+В') (для обхода по часовой стрелке). Этот контур охватывает положительный ток величины j_лин α.

 

Должно выполняться равенство 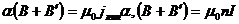(после сокращения на α и замены). Из этого равенства следует, что поле как внутри, так и снаружи бесконечного соленоида является конечным. Возьмем плоскость, перпендикулярную к оси соленоида (рис. 50.5 Сав 151). Вследствие замкнутости линий В магнитные потоки через внутреннюю часть S этой плоскости и через внешнюю часть S' должны быть одинаковыми. Поскольку поля однородны и перпендикулярны к плоскости, каждый из потоков равен произведению соответствующего значения магнитной индукции и площади, пронизываемой потоком. Таким образом, получается соотношение BS=B'S'. Левая часть этого равенства конечна, множитель S' в правой части бесконечно большой. Отсюда следует, что В'=0.

Итак, мы доказали, что вне бесконечно длинного соленоида магнитная индукция равна нулю. Внутри соленоида поле однородно.

Положив В'=0, придем к формуле для магнитной индукции внутри соленоида: . Произведение nI называется числом ампер-витков на метр. При n = 1000 витков на метр и силе тока в 1 А магнитная индукция внутри соленоида составляет 4π10^-4 Тл (Тесла) =4π Гс (Гаусса).

В магнитную индукцию на оси соленоида симметрично расположенные витки вносят одинаковый вклад. Поэтому у конца полубесконечного соленоида на его оси магнитная индукция равна половине значения: .

Практически, если длина соленоида значительно больше, чем его диаметр, формула будет справедлива для точек в средней части соленоида, а формула — для точек на оси вблизи его концов.