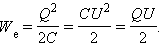Энергия электрического поля. Закон Джоуля – Ленца

Опыт показывает, что заряженный конденсатор содержит запас энергии.

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Процесс зарядки конденсатора можно представить как последовательный перенос достаточно малых порций заряда Δq > 0 с одной обкладки на другую (рис. 1.7.1). При этом одна обкладка постепенно заряжается положительным зарядом, а другая – отрицательным. Поскольку каждая порция переносится в условиях, когда на обкладках уже имеется некоторый заряд q, а между ними существует некоторая разность потенциалов при переносе каждой порции Δq внешние силы должны совершить работу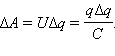

Энергия Wе конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q:

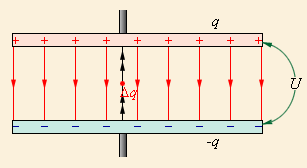Рисунок 1.7.1. Процесс зарядки конденсатора

Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением Q = CU.

Электрическую энергию Wе следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. Формулы для Wе аналогичны формулам для потенциальной энергии Eр деформированной пружины (см. ч. I, § 2.4)

где k – жесткость пружины, x – деформация, F = kx – внешняя сила.

По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Это легко проиллюстрировать на примере заряженного плоского конденсатора.

Напряженность однородного поля в плоском конденсаторе равна E = U/d, а его емкость.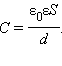

Поэтому

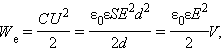где V = Sd – объем пространства между обкладками, занятый электрическим полем. Из этого соотношения следует, что физическая величина

является электрической (потенциальной) энергией единицы объема пространства, в котором создано электрическое поле. Ее называют объемной плотностью электрической энергии.

Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности wе по всему объему, в котором создано электрическое поле.

При протекании тока упорядоченное движение электронов поддерживается за счет энергии электрического поля. В результате соударений с ионами кристаллической решетки электроны передают свою энергию движения этим ионам и увеличивают скорость их хаотических тепловых колебаний. Таким образом, энергия движения электронов в результате столкновений с ионами приводит к нагреванию решетки, и протекание тока в проводнике должно сопровождаться выделением тепловой энергии. Джоуль и Ленц независимо друг от друга экспериментально установили, что количество тепла dQ, выделяющееся в проводнике пропорционально квадрату силы тока I, сопротивлению R проводника и времени dt:

dQ = I2Rdt(2.14)

Закон Джоуля-Ленца можно получить, представляя выделившееся в проводнике тепло как результат работы сил электрического поля по перемещению зарядов внутри проводника. Действительно, за промежуток времени dt по проводнику проходит заряд dq = Idt. Для перемещения этого заряда из одного конца проводника в другой электрическое поле совершает работу dA, которая выражается через разность потенциалов (напряжение) на концах проводника

dA = Udq = UIdt(2.15)

Пусть сопротивление рассматриваемого участка проводника равно R. Тогда, используя закон Ома из (2.15) получим:

dA = I2Rdt = (U2/R)dt(2.16)

Как указано выше эта работа dA пошла на нагревание проводника, то есть dA = dQ и мы в результате пришли к закону Джоуля-Ленца.

Работа тока, совершаемая в единицу времени представляет собой мощность тока. Из (2.15), (2.16) следует, что мощность тока Р равна

P = dA/dt = UI = I2R = U2/R(2.17)

Мощность тока также как и механическая мощность измеряется в ваттах (Вт). 1Вт = 1Дж/с.

Формула (2.14) выражает закон Джоуля-Ленца в интегральной форме, так как отображает тепло, выделившееся во всем объеме рассматриваемого проводника. Найдем теплоту, выделяющуюся малом элементарном объеме dV = dSdlпроводника. Согласно (2.12) сопротивление R этого объема равно r(dl/dS). Пусть j - плотность тока, протекающего через основание dS. По закону Джоуля-Ленца

dQ = I2Rdt = (jdS)2r(dl/dS)dt = rj2dVdt(2.18)

Количество теплоты, выделяющееся в единице объема в единицу времени называют удельной мощностью тока w.

w = dQ/dVdt

Из (2.18)

w = rj2(2.19)

Используя в (2.19) закон Ома в дифференциальной форме (), получим