Тезис Чёрча (Churh’s thesis)
Чтобы хоть как-то осознать строгий математический подход к формальному описанию тезиса Чёрча попробуйте уяснить несколько определений:
1.
Простые основные понятия. Пусть X, Y – два множества. Частичной функцией (или отображением) из X в Y будем называть любую пару {D(f), f}, состоящую из подмножества D(f) 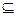 X и отображения f: D(f)
X и отображения f: D(f) 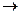 Y. Здесь D(f) называется областью определения f; f определена в точке x
Y. Здесь D(f) называется областью определения f; f определена в точке x 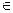 X, если x
X, если x 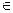 D(f); f нигде не определена если D(f) пусто; существует единственная нигде не определённая частичная функция.
D(f); f нигде не определена если D(f) пусто; существует единственная нигде не определённая частичная функция.
Через Z 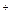 ={1, 2, 3, …} обозначим множество натуральных чисел. Если n
={1, 2, 3, …} обозначим множество натуральных чисел. Если n 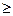 1, через (Z
1, через (Z 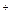 )
) 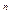 условимся обозначать n-кратное прямое произведение Z
условимся обозначать n-кратное прямое произведение Z 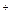 на себя, т.е. множество упорядоченных n-наборов
на себя, т.е. множество упорядоченных n-наборов 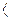 x
x 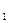 , x
, x 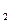 , …, x
, …, x 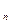
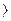 , x
, x 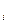
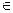 Z
Z 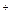 . Основным объектом определения будут «целочисленные» частичные функции (Z
. Основным объектом определения будут «целочисленные» частичные функции (Z 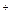 )
) 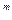 в (Z
в (Z 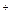 )
) 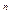 для различных m, n.
для различных m, n.
В следующей далее классификации этих функций по степени их вычислимости под словом «программа» вы можете представлять себе программу для универсальной вычислительной машины (компьютера), написанную без учёта ограничений на время и память. Для простоты подразумевается, что каждая такая программа для вычисления функции содержит специальное «пустое место» для вставки очередного значения аргумента.
2.
Основные определения.
2.1. Частичная функция f из (Z 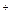 )
) 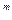 в (Z
в (Z 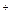 )
) 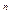 называется вычислимой, если существует такая «программа», что при подаче на её вход вектора x
называется вычислимой, если существует такая «программа», что при подаче на её вход вектора x 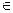 (Z
(Z 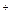 )
) 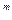 на выходе будет получена f(x), если x
на выходе будет получена f(x), если x 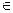 D(f), либо
D(f), либо 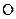 , если x
, если x 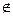 D(f). (Здесь символ
D(f). (Здесь символ 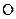 - указатель того, что f не определена, т.е. вычисление не производится).
- указатель того, что f не определена, т.е. вычисление не производится).
2.2. Частичная функция f из (Z 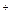 )
) 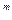 в (Z
в (Z 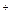 )
) 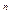 называется полувычислимой, если существует такая «программа», что при подаче на её вход вектора x
называется полувычислимой, если существует такая «программа», что при подаче на её вход вектора x 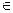 (Z
(Z 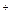 )
) 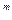 на выходе будет получена f(x), если x
на выходе будет получена f(x), если x 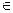 D(f), либо получаем на выходе или же программа работает бесконечно долго, если x
D(f), либо получаем на выходе или же программа работает бесконечно долго, если x 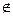 D(f). (Для математических эстетов заметим: в частных случаях получается, что все вычислимые функции полувычислимы, а всюду определённые полувычислимые функции вычислимы).
D(f). (Для математических эстетов заметим: в частных случаях получается, что все вычислимые функции полувычислимы, а всюду определённые полувычислимые функции вычислимы).
2.3. Частичная функция f называется невычислимой, если она не удовлетворяет условиям из пп. 2.1. и 2.2.
3.
 2017-10-31
2017-10-31 382
382







