2018-01-08
2748
Типовые задачи с решениями и для самостоятельного решения
По теме «Электрическое поле в веществе»
Типовые задачи с решениями
Задача 1. Вычислить электрический момент p диполя, если его заряд q=10 нКл, плечо l =0,5 см
| Дано: q=10нКл l=0,5 см | СИ 10-8 Кл 5×10-3 м |
| p-? |
Решение:
p=q×l
p=10-8 ×5×10-3 =5 × 10-11 Кл×м
Ответ: р=5 × 10-11 Кл×м.
Задача 2. Электростатическое поле создано точечным зарядом q0=10e в воде (ε=80). При перемещении положительного заряда q из точки А, находящейся на расстоянии r1 =0,1 мм от заряда q0, в точку В, находящуюся на расстоянии r2 =0,2 мм от заряда q0, силами электрического поля совершена работу 0,1 мкДж. Найти величину заряда q.
| Дано: q0=10e e=1,6×10-19Кл r1=0,1 мм r2=0,2 мм А=0,1 мкДж | СИ 10-4 м 2×10-4 м 10-7 Дж |
| q-? |
Решение:
Потенциал электрического поля, созданного точечным зарядом q0 в воде:
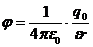
Работа электрического поля по перемещению положительного заряда q из точки А в точку В равна:
A = -q ·Δφ
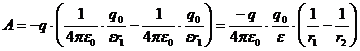
Выразим из полученного выражения q:
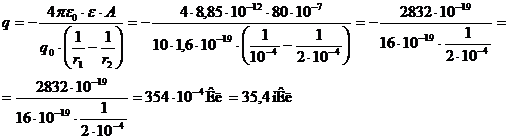
Ответ: q=35,4 мКл.
Задача 3. Два точечных заряда Q1=2Q и Q2=-Q находятся на расстоянии d друг от друга в среде с относительной диэлектрической проницаемостью ε. Найти положение точки на прямой, проходящей через эти заряды, напряженность E поля в которой равна нулю.
| Дано: Q1=2Q Q2=-Q d, ε | СИ |
| r-? |
Решение:
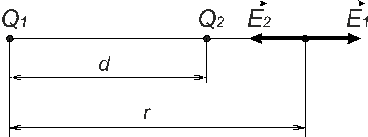
Напряженность, создаваемая зарядами Q1 и Q2 в искомой точке r по условию задачи равна нулю:
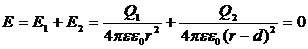
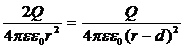
2(r-d)2 = r2
2r2 - 4rd + 2d2 = r2
r2 - 4rd + 2d2 = 0
Решение полученного квадратного уравнения:
D = 16d2 - 8d2 = 8d2;
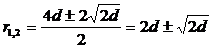
Поскольку d<r, получаем
r = (2+√2)d
Ответ: r = (2+√2)d.
Задача 4. Прямой металлический стержень диаметром d =5 см и длиной l =4 м, находящийся в жидком диэлектрике (ε = 10), несет равномерно распределенный по его поверхности заряд Q=500 нКл. Определить напряженность E поля в точке, находящейся против середины стержня на расстоянии a =1 см от его поверхности.
| Дано: d=5 см l=4 м ε=10 Q=500 нКл a=1 см | СИ 5×10-2 м 5×10-7 Кл 10-2 м |
| E-? |
Решение:
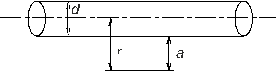
Линейная плотность заряда τ = Q / l.
Напряженность поля, создаваемого стержнем, на расстоянии r от оси симметрии стержня:
,
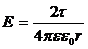Учитывая, что r = a + d / 2, получаем:
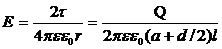
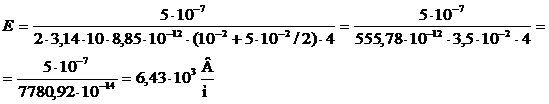
Ответ: Е=6,43 × 103 В/м.
Задача 5. В жидком диэлектрике (ε=10) вертикально расположена большая металлическая пластина, соединенная с землей. На расстоянии a =10 см от пластины находится неподвижная точка, к которой на нити длиной l =12 см подвешен маленький шарик массой m=0,1 г. При сообщении шарику заряда Q он притянулся к пластине, в результате чего нить отклонилась от вертикали на угол α=30°. Найти заряд Q шарика.
| Дано: m=0,1 г l=12 cм ε=10 a=10 см α=30º | СИ 10-4 кг 12×10-2 м 0,1 м |
| Q-? |
Решение:
На шарик действуют следующие силы: сила тяжести mg, сила электрического взаимодействия с пластиной F и сила натяжения нити T. Они уравновешивают друг друга на некотором расстоянии r от пластины.
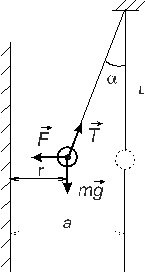Это расстояние можно определить следующим образом:
r = a – l ·sin α.
Проекция силы T на ось Ox:
Fт=mg·sin α.
Сила электрического взаимодействия шарика и пластины:
.
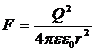Приравняем эти силы:
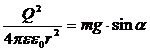
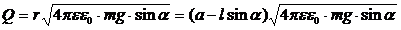
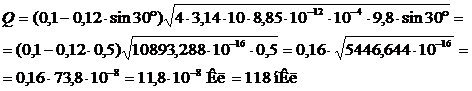
Ответ: Q=118 нКл.
