Контрольная работа №6 по разделу «атомная и ядерная физика»

Задача 1. Определить длину волны излучения, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на второй.

Дано: n1 =2; n2 = 3. -?

Решение:

Воспользуемся сериальной формулой для атома водорода

= ,

где E_i - энергия ионизации; n₁ - номер орбиты, на которую перешел электрон; n₂ - номер орбиты, с которой перешел электрон.

Энергия фотона связана с длиной волны излучения соотношением = . Сопоставляя две формулы для , находим выражение для длины волны: =hc/ .

Подставим значения величин: E_i =13,6 эВ = 13,6×1,.6×10^-19 Дж, h = 6,63×10^-34 Дж×с, c = 3×10⁸ м/с, n₁ =2, n₂ = 3 и проведем вычисления:

= 6,63×10^-34 ×3×10⁸ /[13,6×1.6×10^-19 (1/4-1/9)] м = 6,58×10^{-7 м = 0,658 мкм.}

 

Ответ: = 0,658 мкм

Задача 2. Вычислить длину волны де Бройля для протона, прошедшего ускоряющую разность потенциалов U = 10 В.

Дано : U=10 В. -?

Решение:

Длина волны де Бройля определяется по формуле = , где h - постоянная Планка, р - импульс частицы. После прохождения протоном разности потенциалов U его кинетическая энергия Тстановится равной eU. Так как величина Т гораздо меньше энергии покоя протона (938 МэВ), то для импульса протона можно воспользоваться нерелятивистским соотношением р=mv. При этом Т = р²/2m. После преобразований находим:

р² = 2mТ, р = (2meU)^1/2, =h/ (2meU)^1/2.

Подставим значения величин: е =1,6×10^-19 Кл, h = 6,63×10^-34 Дж×с, m = 1,672×10^{-27 кг и проведем вычисления:}

=6,63×10^-34 /(2×1,672×10^-27×1,6×10^-19 10)^1/2 м =9,1×10^{-12 м = 9,1 пм.}

 

Ответ: = 9,1 пм.

Задача 3. Кинетическая энергия валентного электрона в некотором атоме составляет величину порядка 5 эВ. Оценить минимальные размеры атома, используя соотношение неопределенностей.

Дано: Т =5 эВ. -?

Решение:

Воспользуемся соотношением неопределенностей для координаты и импульса, которое имеет вид: p_x x ³ћ, где x - неопределенность координаты х; p_x - неопределенность соответствующей проекции импульса, ћ - постоянная Планка. При оценке размеров атома можно считать, что неопределенность координаты валентного электрона сравнима с линейными размерами атома: x ~ , а неопределенность импульса p_x сравнима с самим импульсом: p_x ~ р ~ (2mТ)^1/2, где Т = р²/2m - кинетическая энергия электрона. После преобразований находим:

(2mТ)^1/2 ³ћ, ~ ћ/(2mТ)^1/2.

Подставим значения Т=50×1,6×10^-19 Дж, ћ = 1,05×10^-34 Дж×с, m = 9,11×10^{-31 кг и проведем вычисления:}

~1,05×10^-34/(2×9,11×10^-31×5×1,6×10^-19)^1/2 м = 8,7×10^{-11 м.}

 

Ответ: ~ 8,7×10^{-11 м.}

Задача 4. Электрон в бесконечно глубоком одномерном прямоугольном потенциальном ящике находится в основном состоянии. Какова вероятность обнаружения электрона в средней трети ящика?

Дано: 1/3 £ x/ £2/3. w -?

Решение:

Вероятность обнаружения электрона в некотором интервале от х₁ до х₂ равна w = 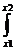| |² dx, где - волновая функция электрона, которая в случае бесконечно глубокого одномерного прямоугольного потенциального ящика может быть представлена в виде (х)=(2/ )^0.5sin( x/ ).

В результате интегрирования находим:

w=(2/ ) 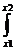|sin( x/ )|²dx =

=(2/ ) |sin y|²dy( / )=(1/ ) [y-siny cosy] .

Здесь проведена замена переменных x/ Þ y. В нашем случае x₁= /3, x₂=2 /3, и, следовательно, y₁= /3, y₂ = 2 /3. В результате вычислений находим w = 0,609.

 

Ответ: w = 0,609.

Задача 5. Записать электронную конфигурацию атома фосфора c вакансией в 2р -подоболочке.

Дано: атом фосфора Р с вакансией в 2р - подоболочке. Электронная конфигурация?

 

Решение:

 

Нейтральный атом фосфора Р имеет пятнадцать электронов, которые распределены по подоболочкам следующим образом: 1s² 2s² 2p⁶ 3s² 3p³. При отсутствии одного из электронов в 2р -подоболочке конфигурация электронов приобретает вид: 1s² 2s² 2p⁵ 3s² 3p³.

 

 

Ответ: 1s² 2s² 2p⁵ 3s² 3p³.

 

Задача 6. Определить среднюю энергию _ср свободных электронов в металле при абсолютном нуле температур.

Дано: Т= 0 К. ср -?

 

Решение:

 

Воспользуемся формулой для распределения свободных электронов в металле при 0 К: dn()=(2m)^{3/2 1/2}d /2 ²ћ³, где dn() - концентрация электронов, энергия которых заключена в пределах от до +d . Для определения средней энергии _ср нужно найти отношение ò dn()/òdn(), где интегрирование по энергии в обоих интегралах нужно проводить в пределах от нуля до энергии Ферми _F. Значение верхнего интеграла равно (2m/ћ²)^3/2 _F^5/2/[5 ²], а нижнего - (2m/ћ²)^3/2 _F^3/2/[3 ²]. Отсюда находим, что _ср =3 _F/5.

 

Ответ: _ср =3 _F/5.

 

Задача 7. Найти энергию связи, приходящуюся на один нуклон в ядре трития ³H.

Дано: ядро трития 1H3. Eсв/А -?

 

Решение:

 

Для определения энергии связи, приходящейся на один нуклон, найдем вначале полную энергию связи ядра. Для этого воспользуемся соотношением E_св = c² m, где дефект массы m=Zm_p+(A-Z)m_n- -m_я; Z- число протонов в ядре; А - число нуклонов в ядре;

m_p- масса протона; m_n - масса нейтрона; m_я - масса ядра. Если вместо масс ядер использовать массы соответствующих атомов, то величину m можно представить в виде m = Z(m_p+m_е)+ (A-Z)m_n - m_а.

Энергия связи, приходящаяся на один нуклон, E_св/А= c² m/А. Если значения масс подставлять в атомных единицах массы, а величину c² выразить в единицах МэВ/а.е.м., то энергию связи, приходящуюся на один нуклон и выраженную в МэВ, получим с помощью соотношения

E_св/А= 931 m/А=931[Z(m_p+m_е)+ (A-Z)m_n - m_а]/А.

Подставим значения величин и проведем вычисления: m_p=1,00728 а.е.м., m_e=0,00055 а.е.м., m_n=1,00867 а.е.м., m_Н=3,01605 а.е.м., Z=1, A=3, E_св/А=931[1,00728+0,00055+2×1,00867– 3,01605]/3 МэВ = 2,83 МэВ.

 

Ответ: E_св/А= 2,83 МэВ.

 

Задача 8. Период полураспада атомов некоторого радиоактивного вещества Т _1/2 =2,0 с. Определить вероятность Р того, что ядро не распадется на промежутке времени t, равном 10,0 с.

Дано : Т 1/2 =2,0 с; t =10,0 с. Р -?

 

Решение:

 

Вероятность Р можно определить с помощью отношения Р = N/N₀, где N - число ядер, не распавшихся к моменту времени t; N₀ - исходное число ядер. Для нахождения отношения N/N₀ воспользуемся законом радиоактивного распада N= N₀ exp(- t), где - постоянная радиоактивного распада. Период полураспада связан с величиной соотношением T_1/2 =0,693/ . После преобразований находим:

Р = exp(- t)= exp(-0,693t/T_1/2).

Подставим значения величин и проведем вычисления:

Р = exp(-0,693×10,0/2,.0) = exp(-3,465)=0,031.

 

Ответ: Р =0,031.