Исследовать устойчивость линеаризованной системы можно любым из известных методов. В инженерной практике широко используются аналитические критерии оценки устойчивости (например, критерий Гурвица) или частотные методы. Использование критерия Гурвица удобно для систем не выше 4-го порядка, он позволяет судить не только об устойчивости исследуемой системы при фиксированных значениях ее параметров, но и о влиянии каждого из них. Частотные методы теоретически не накладывают ограничений на порядок системы, однако оценка влияния входящих параметров на ее устойчивость связана с трудоемкими построениями частотных характеристик.
По критерию Гурвица гидромеханическая система управления будет устойчива тогда и только тогда, когда положительны все 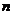 определителей, составленных из коэффициентов характеристического уравнения системы.
определителей, составленных из коэффициентов характеристического уравнения системы.
Характеристическое уравнение гидромеханической системы управления, определяющее устойчивость, на основании выражения передаточной функции запишется в виде:
|
|
|
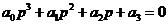 (86)
(86)
где 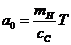 ,
, 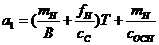 ,
, 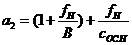 ,
, 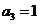 .
.
В соответствии с критерием Гурвица, для устойчивости гидромеханической следящей системы управления необходимо, чтобы все коэффициенты уравнения были положительными, и соблюдалось условие 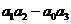 >0, или
>0, или 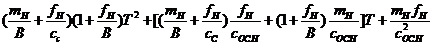 >
> 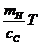 . (87)
. (87)
В частном случае, когда 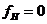 условие устойчивости следящей системы управления упрощается и выражается формулой
условие устойчивости следящей системы управления упрощается и выражается формулой
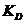 <
< 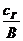 (88)
(88)
Выражение (70) накладывает ограничение на величину коэффициента добротности гидромеханической системы управления с отрицательным коэффициентом передачи. Оно показывает, что для устойчивости системы управления с учетом принятых допущений необходимо, чтобы коэффициент добротности не превышал отношения жесткости «гидравлической пружины» силового гидроцилиндра системы управления к жесткости механической характеристики дроссельного привода системы управления.
Рассмотрим устойчивость разработанной гидромеханической следящей системы управления (рис.7) применительно к типовой шахтной однобарабанной подъемной установке Ц2,5х2АР оснащенную безредукторным гидравлическим приводом.
На основании статического расчета элементов следящей системы управления определены ее исходные конструктивные параметры и основные характеристики, которые представлены в табл. 1.
Таблица 1
Исходные данные для расчета системы управления на устойчивость
 -масса проводки управления -масса проводки управления
| 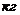
| ||
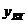 -координата перемещения входного звена системы управления -координата перемещения входного звена системы управления
|
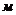
| 0,4 | |
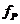 -коэф. вязкого трения проводки управления -коэф. вязкого трения проводки управления
| 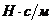
| 4·102 | |
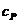 -жесткость проводки управления -жесткость проводки управления
| 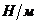
| 5·104 | |
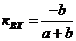 -коэф. передачи по входному сигналу -коэф. передачи по входному сигналу
| - | 0,5 | |
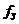 -коэф. вязкого трения золотника -коэф. вязкого трения золотника
| 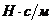
| 0,5·103 | |
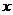 -перемещение плунжера золотника -перемещение плунжера золотника
| 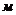
| 4·10-3 | |
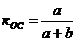 -коэффициент обратной связи -коэффициент обратной связи
| _ | 0,5 | |
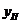 -перемещение поршня -перемещение поршня
| 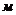
| 10·10-3 | |
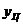 -перемещение цилиндра -перемещение цилиндра
| 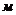
| 0,15·10-6 | |
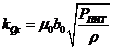 -коэффициент усиления по расходу -коэффициент усиления по расходу
| 
| 0,716 | |
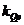 -коэф. скольжения золотника по расходу -коэф. скольжения золотника по расходу
| 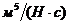
| 8,5·10-12 | |
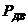 -перепад давления на гидроцилиндре (макс.) -перепад давления на гидроцилиндре (макс.)
| 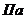
| 4,7·106 | |
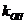 -коэф. объемных потерь на гидроцилиндре -коэф. объемных потерь на гидроцилиндре
| 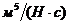
| 0,3·10-5 | |
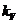 -коэф. сжимаемости рабочей жидкости -коэф. сжимаемости рабочей жидкости
| МПа | 7,14·10-4 | |
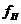 -коэф. вязкого трения поршня -коэф. вязкого трения поршня
| 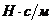
| 0.1·106 | |
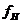 -коэф. вязкого демпфирования нагрузки -коэф. вязкого демпфирования нагрузки
| 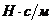
| 2·104 | |
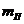 -приведенная масса поршня и жидкости в гидроцилиндре и гидролиниях -приведенная масса поршня и жидкости в гидроцилиндре и гидролиниях
|
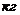
| 7,5 | |
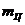 -приведенная масса гидроцилиндра -приведенная масса гидроцилиндра
| 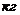
| 6,5 | |
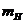 -масса нагрузки -масса нагрузки
| 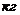
| ||
 -коэф. жесткости основания гидроцилиндра -коэф. жесткости основания гидроцилиндра
| 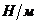
| 7∙1010 | |
 -жесткость рабочего органа нагрузки -жесткость рабочего органа нагрузки
| 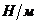
| 3,9·105 | |
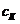 -жесткость силовой проводки -жесткость силовой проводки
| 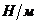
| 1,0·107 | |
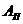 и и 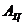 -рабочая площадь поршня и цилиндра исполнительного органа системы управления -рабочая площадь поршня и цилиндра исполнительного органа системы управления
|
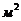
| 0,02355 | |
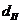 -диаметр поршня гидроцилиндра -диаметр поршня гидроцилиндра
| 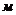
| 0,03 | |
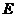 -приведенный модуль упругости жидкости -приведенный модуль упругости жидкости
| 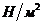
| 1,4·109 | |
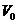 -объем жидкости в рабочей камере цилиндра -объем жидкости в рабочей камере цилиндра
| 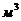
| 1·10-4 | |
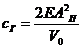 -жесткость гидравлической пружины исполнительного гидроцилиндра -жесткость гидравлической пружины исполнительного гидроцилиндра
|
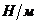
| 1,55·1010 | |
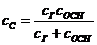 -коэффициент обобщенной жесткости гидромеханической системы управления -коэффициент обобщенной жесткости гидромеханической системы управления
|
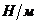
| 1,26·1010 | |
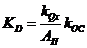 -коэффициент добротности следящей системы управления -коэффициент добротности следящей системы управления
|

| 21,7 | |
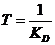 -постоянная времени системы управления -постоянная времени системы управления
|

| 0,046 | |
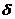 -радиальный зазор в золотнике -радиальный зазор в золотнике
| 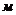
| 40-5 | |
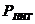 -давление питания системы управления -давление питания системы управления
| 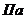
| 5·106 | |
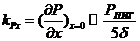 -коэф. усиления по давлению -коэф. усиления по давлению
| 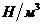
| 0,025·1012 | |
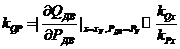 -коэффициент скольжения по расходу -коэффициент скольжения по расходу
|
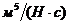
| 28,64·10-12 | |
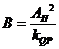 -коэф. жесткости механической характеристики дроссельной системы управления -коэф. жесткости механической характеристики дроссельной системы управления
|
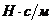
| 19,36·106 | |
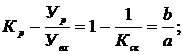 коэффициент передачи коэффициент передачи
| - | 0,25 |
|
|
|
Запишем характеристическое уравнение гидромеханической системы управления, определяющее устойчивость, в виде:
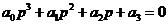 (89)
(89)
где 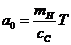 ,
, 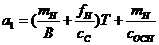 ,
, 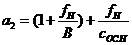 ,
, 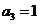 - коэффициенты характеристического уравнения.
- коэффициенты характеристического уравнения.
Определим значения этих коэффициентов.
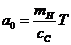 =
= 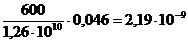 ,
,
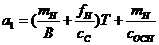 =
= 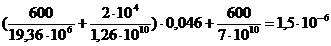
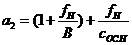 =
= 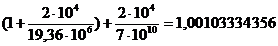 ;
; 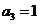 .
.
Как видно, коэффициенты характеристического уравнения все положительные. Проверим соблюдение условия 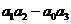 >0.
>0.
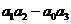 =1,5·10-6×1,00103334356– 2,19·10-9×1=1,5·10-6>0. Следовательно, необходимое условие соблюдается. Поэтому система управления устойчивая.
=1,5·10-6×1,00103334356– 2,19·10-9×1=1,5·10-6>0. Следовательно, необходимое условие соблюдается. Поэтому система управления устойчивая.
Проверим устойчивость системы управления по уравнению
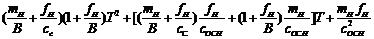 >
> 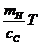 (90)
(90)
Подставим, численные значения параметров в это выражение, получим:
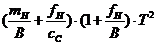 =
= 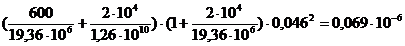 ;
;
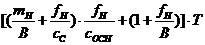 =
= 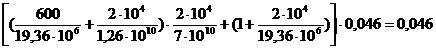 ;
;
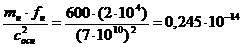 ;
;
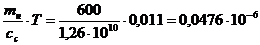 .
.
В результате выполненных операций получим соотношение
0,069·10-6 > 0,0476·10-6
Таким образом, условие устойчивости по уравнению выполняется.
Для частного случая, если бы коэффициент вязкого демпфирования 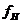 нагрузки был бы равен нулю, то условие устойчивости определялось бы по выражению
нагрузки был бы равен нулю, то условие устойчивости определялось бы по выражению 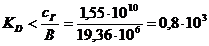
Следовательно, при 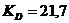 < 800 условие устойчивости также выполняется.
< 800 условие устойчивости также выполняется.
 2018-01-21
2018-01-21 412
412








