| Ауд. | Л-3, Гл. 2 | № 163, 164, 166, 187, 191, 192. |
☺ ☻ ☺
Элементарными преобразованиями матрицы называют следующие преобразования:
1) умножение строки или столбца на число, отличное от нуля;
2) прибавление к одной строке (столбцу) другой строки (столбца), умноженной на любое число;
3) перестановка двух строк (столбцов).
Элементарные преобразования не меняют ранга матрицы.
•• ☻☻ ••
Пример 1 – 163: Найти ранг матрицы:  =
= 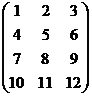 при помощи элементарных преобразований.
при помощи элементарных преобразований.
Решение:
1). Применим элементарные преобразования к заданной матрице:
 = (1) →
= (1) → 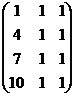 = (2) →
= (2) →  = (3) →
= (3) →  .
.
Операции: (1): [C3]–[C2]; [C2]–[C1]. (2): [R4]–[R3]; [R3]–[R2]; [R2]–[R1] делим на число 3 строки матрицы 2,3,4. (3): [C3]–[C2]; [R4]–[R3]; [R3]–[R2]; [R2]–[R1].
2). Видим (!): ранг матрицы равен 2.
Ответ: 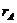 = 2.
= 2.
Пример 2 – 164: Найти ранг матрицы: 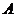 =
= 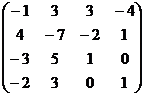 при помощи элементарных преобразований.
при помощи элементарных преобразований.
Решение:
1). Применим элементарные преобразования к заданной матрице:
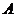 = (1) →
= (1) → 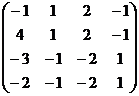 = (2) →
= (2) → 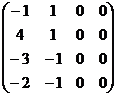 = (3) →
= (3) →  = (4) →
= (4) →  .
.
Операции: (1): [C4]+[C3]; [C3]+[C1]; [C3]+[C1]∙2. (2): [C4]+[C3]; [C3]–[C2]∙2. (3): [R4]–[R3]; [R3]+[R2]; [R2]–[R1], разделим [R2] на 5. (4) действия очевидны.
2). Видим (!): ранг матрицы равен 2.
Ответ: 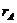 = 2.
= 2.
Пример 3 – 166: Найти ранг матрицы: 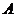 =
= 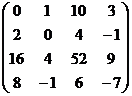 при помощи элементарных преобразований.
при помощи элементарных преобразований.
Решение:
1). Применим элементарные преобразования к заданной матрице:
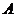 = (1) →
= (1) → 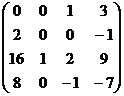 = (2) →
= (2) → 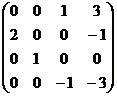 = (3) →
= (3) →  = (4) →
= (4) →  .
.
Операции: (1): [C3]–[C1] и разделить на 10; [C2]–[C3] и делим на 2. (2): используя [C2] чистим строку-3, [R4]–[R2]∙4. (3): [C4]+[C1], используя [C3] чистим строку-1, используя [C4] чистим строку-2. (4) действия очевидны.
2). Видим (!): ранг матрицы равен 3.
Ответ: 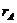 = 3.
= 3.
Пример 4 – 187: Решить систему уравнений: 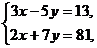 по правилу Крамера.
по правилу Крамера.
Решение:
1). Составим определитель системы: d = 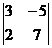 и определители:
и определители: 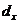 =
= 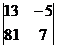 , заменяя 1-й столбец определителя d столбцом
, заменяя 1-й столбец определителя d столбцом 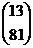 правой части;
правой части; 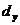 =
= 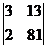 , заменяя 2-й столбец определителя d столбцом
, заменяя 2-й столбец определителя d столбцом 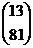 правой части.
правой части.
2). Вычислили: d =31, 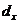 = 496,
= 496, 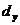 =217.
=217.
3). Применяя правило Крамера, получим: x = 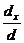 =16; y =
=16; y = 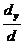 =7.
=7.
Ответ: x =16; y =7.
Пример 5 – 191: Решить систему уравнений: 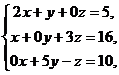 пользуясь формулами Крамера.
пользуясь формулами Крамера.
Решение:
1) Системе уравнений соответствуют: матрица системы A и расширенная матрица 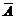 :
:
A = 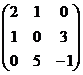 ,
, 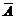 =
= 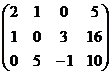 .
.
2) Формулы Крамера в общем виде: 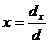 ,
, 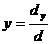 ,
, 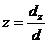 . Вычислим все величины, входящие в эти формулы, для заданной системы уравнений:
. Вычислим все величины, входящие в эти формулы, для заданной системы уравнений:
d = 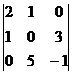 = –29,
= –29, 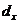 =
= 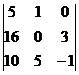 = –29,
= –29, 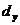 =
= 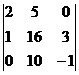 =–87,
=–87, 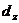 =
= 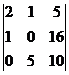 = –145.
= –145.
3) Вычислим неизвестные: 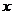 =1,
=1, 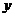 =3,
=3, 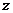 =5 → решение заданной системы уравнений.
=5 → решение заданной системы уравнений.
Ответ: 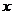 =1,
=1, 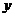 =3,
=3, 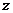 =5.
=5.
Пример 6 – 192: Решить систему уравнений: 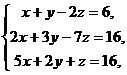 пользуясь формулами Крамера.
пользуясь формулами Крамера.
Решение:
1) Системе уравнений соответствуют: матрица системы A и расширенная матрица 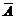 :
:
A = 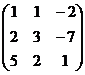 ,
, 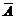 =
= 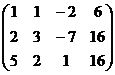 .
.
2) Формулы Крамера в общем виде: 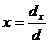 ,
, 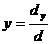 ,
, 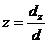 . Вычислим все величины, входящие в эти формулы, для заданной системы уравнений:
. Вычислим все величины, входящие в эти формулы, для заданной системы уравнений:
d = 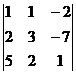 = 2,
= 2, 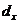 =
= 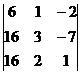 = 6,
= 6, 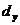 =
= 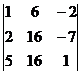 =–87,
=–87, 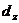 =
= 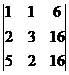 = –145.
= –145.
3) Вычислим неизвестные: 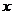 =3,
=3, 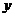 =1,
=1, 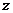 =−1 → решение заданной системы уравнений.
=−1 → решение заданной системы уравнений.
Ответ: 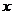 =3,
=3, 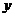 =1,
=1, 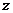 =−1.
=−1.
* * * * * * * * * *
Домашнее задание
| Ауд. | Л-3, Гл. 2 | № 165, 168, 188, 190. |
Пример 1 – 165: Найти ранг матрицы: 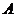 =
= 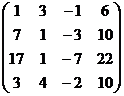 при помощи элементарных преобразований.
при помощи элементарных преобразований.
Решение:
1). Применим элементарные преобразования к заданной матрице:
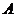 = (1) →
= (1) → 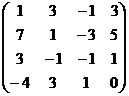 = (2) →
= (2) → 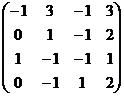 = (3) →
= (3) →  = (4) →
= (4) →  .
.
Операции: (1): [R3]–[R2]∙2; [R4]–[R2], делим [C4] на 2. (2): [C1]–[C4], делим [C1] на 2; [R4]–[R1]∙2, делим [C4] на 3; [R2]+[R1], делим [C2] на 4. (3): [C4]+[C2], делим [C4] на 4, используя [R4] чистим столбец-4; [R1]+[R3], делим [R1] на 2. (4) действия очевидны.
2). Видим (!): ранг матрицы равен 2.
Ответ: 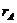 = 2.
= 2.
Пример 2 – 168: Найти ранг матрицы: 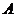 =
= 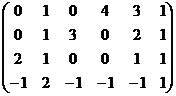 при помощи элементарных преобразований.
при помощи элементарных преобразований.
Решение:
1). Применим элементарные преобразования к заданной матрице:
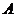 = (1) →
= (1) → 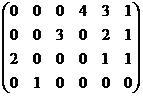 = (2) →
= (2) →  = (3) →.
= (3) →.
Операции: (1): [C2]–[C6], используя [C2] чистим строку-4. (2): используя [C1] чистим строку-3, используя [C3] чистим строку-2, используя [C4] чистим строку-1. (3): действия очевидны.
2). Видим (!): ранг матрицы равен 4.
Ответ: 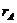 = 4.
= 4.
Пример 3 – 188: Решить систему уравнений: 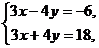 по правилу Крамера.
по правилу Крамера.
Решение:
1). Составим определитель системы: 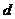 =
= 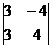 и определители:
и определители: 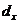 =
= 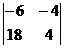 , заменяя 1-й столбец определителя:
, заменяя 1-й столбец определителя: 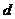 столбцом
столбцом 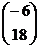 правой части;
правой части; 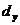 =
= 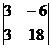 , заменяя 2-й столбец определителя
, заменяя 2-й столбец определителя 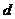 столбцом
столбцом 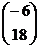 правой части.
правой части.
2). Вычислили: 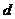 =24,
=24, 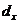 = 48,
= 48, 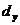 =72.
=72.
3). Применяя правило Крамера, получим: 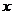 =
= 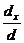 =2;
=2; 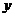 =
= 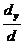 =3;
=3; 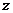 =
= 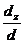 =3.
=3.
Ответ: 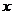 =2;
=2; 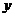 =3.
=3.
Пример 4 – 190: Решить систему уравнений: 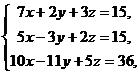 пользуясь формулами Крамера.
пользуясь формулами Крамера.
Решение:
1) Системе уравнений соответствуют: матрица системы A и расширенная матрица 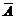 :
:
A = 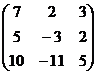 ,
, 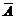 =
= 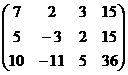 .
.
2) Формулы Крамера в общем виде: 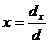 ,
, 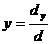 ,
, 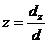 . Вычислим все величины, входящие в эти формулы, для заданной системы уравнений:
. Вычислим все величины, входящие в эти формулы, для заданной системы уравнений:
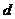 =
= 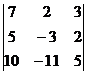 = –36,
= –36, 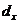 =
= 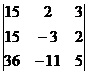 = –72,
= –72, 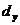 =
= 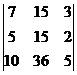 =36,
=36, 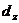 =
= 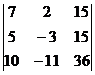 = –36.
= –36.
3) Вычислим неизвестные: 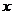 =2,
=2, 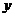 =–1,
=–1, 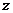 =1 → решение заданной системы уравнений.
=1 → решение заданной системы уравнений.
Ответ: 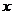 =2,
=2, 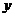 =–1,
=–1, 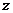 =1.
=1.
•• ☻☻ ••
Вопросы для самопроверки:
1. Можно ли, применяя правило Крамера, провести полное исследование решений системы линейных уравнений с произвольным числом уравнений и неизвестных?
2. Можно ли решить систему уравнений по правилу Крамера, если все значения свободных членов b i, i = 1,2, …, n равны нулю?
 2018-01-21
2018-01-21 214
214






