Тема: Розв’язування математичних задач

Мета роботи: оволодіння навиками розв’язування задач з векторної та лінійної алгебри за допомогою СКМ MATLAB.

Хід роботи.

1. Запустити електронний навчальний посібник.
2. За допомогою навчального посібника виконати наступні приклади.

Приклад 2.1. Створити за допомогою спеціальних символів вектор-рядок 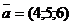і вектор-стовпець 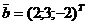(для економії місця вектор-стовпець часто записується як рядок з символом Т, який позначає транспонування).

Розв’язування:

>> A=[4 5 6],B=[2;3;-2]

А =

4 5 6

B =

-2

Приклад 2.2. Створити за допомогою стандартних функцій вектор-стовпець 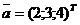і вектор-рядок .

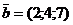Розв’язування:

>> A=vertcat (2,3,4),B=horzcat(2,4,7)

А =

B =

2 4 7

Приклад 2.3. Створити за допомогою спеціальних символів вектор 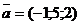та змінити значення координати а₂ на -5.

Розв’язування:

>> A=[2 5 8],A(2)=-5

А =

2 5 8

А =

2 -5 8

Пример 2.4. Створити за допомогою спеціальних символів вектор 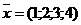та обчислити .

Розв’язування:

>> x=[1 2 3 4];

>> y=sind(x)

y =

 

0.8415 0.9093 0.1411 -0.7568

Приклад 2.5. Перевірити властивості суми векторів, використовуючи вектори , , .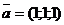

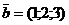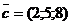Розв’язування:

>> A=[1 1 1];B=[1 2 3];

C=[2 5 8];

>> isequal (A+B,B+A),isequal ((A+B)+C,A+(B+C))

ans =

ans =

Приклад 2.6. Перевірити властивості множення вектора на число за допомогою векторів 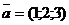і 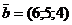та чисел , , .

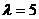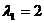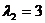Розв’язування:

>> A=[1 2 3];B=[6 5 4];L=5;L1=2;L2=3;

>> A*L+B*L,isequal((A+B)*L,ans)

ans =

35 35 35

ans =

>> (L1*L2)*A,isequal(ans,L1*(L2*A))

ans =

6 12 18

ans =

Приклад 2.7. Обчислити довжину вектора .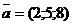

Розв’язування:

>> A=[2 5 8],sqrt(sum(A.*A))

A =

2 5 8

ans =

9.6437

Приклад 2.8. Обчислити одиничний вектор 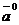, що має однаковий напрям з вектором 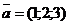. Перевірити, чи є обчислений вектор 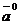одиничним.

Розв’язування:

>> a=[1 2 3];a0=a/sqrt(sum(a.*a))

a0 =

0.2673 0.5345 0.8018

>> sqrt(sum(a0.*a0))

ans =

Координати орта вектора 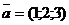дорівнюють (0.2673; 0.5345; 0.8018).

Приклад 2.9. Обчислити кути нахилу вектора 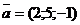до осей координат.

Розв’язування:

>> A=[2 5 -1],acos(A./sqrt(sum(A.*A)))*180./pi

A =

2 5 -1

ans =

68.5833 24.0948 100.5197

sum(cos(ans./180*pi).^2)

ans = 1

Кути нахилу вектора 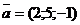α = 68.58°, β = 24.09° і γ=100.52°. При обчисленні кутів нахилу використовувалися оператор поелементного ділення «./». При обчисленні суми квадратів напрямних косинусів використовувався оператор поелементного піднесення до степеня «.^». В результаті сума квадратів направляючих косинусів дорівнює одиниці.

Приклад 2.10. Обчислити роботу, що виконується при прикладанні сили 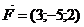в діякій точці, що рухається прямолінійно, переміщуючись із положення 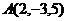в положення .

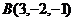Розв’язування:

>> A=[2 -3 5];B=[3 -2 -1];

>> АВ=B-A

АВ =

1 1 -6

>> F=[3 -2 -5];

>> [sum(F.*АВ),dot(F,АВ)]

ans =

31 31

Геометричний зміст скалярного добутку: якщо скалярний добуток дорівнює нулю, то два ненульові вектори ортогональні (перпендикулярні). Якщо скалярний добуток більший нуля, то кут між векторами гострий, якщо менший нуля – тупий.

Приклад 2.11. Обчислити скалярний добуток двох векторів 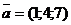і .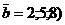

Розв’язування:

>> A=[1 4 7];B=[2 5 8];

[sum(A.*B),dot(A,B)]

ans =

78 78

Скалярний добуток двох векторів 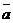і 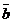, заданих в координатній формі, обчислюється за допомогою стандартної функції dot() абоза допомогою стандартної функції sum() і оператора поелементного множення «. *».

Приклад 2.12. Обчислити кут між векторами 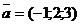і .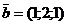

Розв’язування:

>> A=[-1 2 3];B=[1 2 1];

phi=acos(dot(A,B)./(sqrt(sum(A.*A))*

sqrt(sum(B.*B))))

phi =

0.8571

phi=phi*180/pi

phi =

49.1066

Отже, кут між векторами 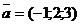і 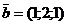дорівнює 49.11° або 0.8571 радіан.

Приклад 2.13. Обчислити векторний добуток векторів 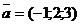і .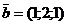

Розв’язування:

>> A=[-1 2 3];B=[1 2 1];C=cross(A,B)

C =

-4 4 -4

Приклад 2.14. Сила 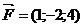прикладена до точки 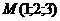. Знайти момент цієї сили відносно точки .

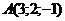Розв’язування:

>>f=[1 -2 4];m=[1 2 3];a=[3 2 -1];

>> am=m-a

am =

-2 0 4

>> mom=cross(am,f)

mom =

8 12 4

 

Приклад 2.15. Знайти мішаний добуток векторів 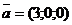, 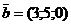і 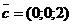, де вектори 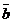і 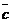перемножуються векторно, а їх результат на вектор 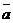- скалярно.

Розв’язування:

>> A=[3 0 0];B=[3 5 0];C=[0 0 2];

ABC=sum(A.*cross(B,C))

ABC =

Приклад 2.16. У тетраедрі з вершинами в точках 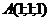, , 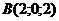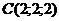і 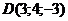обчислити площу тетраедра та трикутника АВС.

Розв’язування:

>> a=[1 1 1];b=[2 0 2];c=[2 2 2];d=[3 4 -3];

>> ab=b-a

ab =

1 -1 1

>> ac=c-a

ac =

1 1 1

>> ad=d-a

ad =

2 3 -4

>> abc=sum(ad.*cross(ab,ac))

abc =

-12

>> V=1/6*abs(abc)

V =

>> c=cross(ab,ac)

c =

-2 0 2

>> d=sqrt(sum(c.*c))

d =

2.8284e+000

>> format short

>> d/2

ans =

1.4142

Приклад 3.1. Створити матрицю А за допомогою спеціальних символів, а матрицю В – за допомогою стандартних функцій.

.

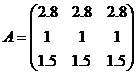
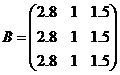Розв’язування:

>> A=[2.8 2.8 28;1 1 1;1.5 1.5 1.5]

A =

2.8000 2.8000 28.0000

1.0000 1.0000 1.0000

1.5000 1.5000 1.5000

>> B=vertcat(horzcat(2.8,1,1.5),horzcat (2.8,1,1.5),...

horzcat(2.8,1,1.5))

B =

2.8000 1.0000 1.5000

2.8000 1.0000 1.5000

2.8000 1.0000 1.5000

Приклад 3.2. Створити матрицю А з прикладу 3.1 і змінити значення елементів, що розташовані на перетині першого рядка і другого стовпця, а також другого рядка і третього стовпця, на 3 і на 5 відповідно. До першого елемента звернутися за допомогою двох індексів, а до другого – за допомогою одного індексу.

Розв’язування:

>> A=[2.8 2.8 28;1 1 1;1.5 1.5 1.5];

>> А(1,2)=3;A(7)=5

А =

2.8000 3.0000 5.0000

1.0000 1.0000 1.0000

1.5000 1.5000 1.5000

Приклад 3.3. Перевірити на рівність наступні матриці:

.

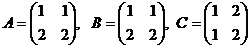Розв’язування:

>> A=[1 1;2 2];B=[1 1;2 2];C=[1 2;2 1];

>> isequal (A,B),isequal (А, З)

ans =

ans =

Приклад 3.4. Транспонувати матрицю .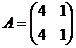

Розв’язування:

>> A=[4 1;4 1]

А =

4 1

4 1

>> A'

ans =

4 4

1 1

>> transpose(A)

ans =

4 4

1 1

Приклад 3.5. Сформувати діагональну матрицю .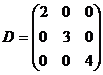

Розв’язування:

>> V=2:4

V =

2 3 4

>> D=diag(V)

D =

2 0 0

0 3 0

0 0 4

Приклад 3.6. Створити одиничну матрицю А (3 х 3), де a₁₁=a₂₂= a₃₃ =1.

Розв’язування:

>> A=eye(3)

А =

1 0 0

0 1 0

0 0 1

Приклад 3.7. Виділити з матриці 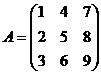нижню і верхню трикутні матриці.

Розв’язування:

>> A=[1 4 7;2 5 8;3 6 9]

А =

1 4 7

2 5 8

3 6 9

>> N=tril(A), V=triu(A)

N =

1 0 0

2 5 0

3 6 9

V =

1 4 7

0 5 8

0 0 9

Приклад 3.8. Створити матрицю Х і піднести кожний її елемент до третього степеня.

Розв’язування:

>> X=[8 5 -3 12;-2 4 -7 1]

X =

8 5 -3 12

-2 4 -7 1

>> X.^3

ans =

512 125 -27 1728

-8 64 -343 1

Приклад 3.9. Виконати додавання матриць .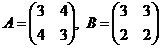

Розв’язування:

>> A=[3 4;4 3];B=[3 3;2 2];A+B

ans =

6 7

6 5

Приклад 3.10. Обчислити добуток матриці А на число 2.

Розв’язування:

>> A=[3 4;4 3];A*2

ans =

6 8

8 6

Приклад 3.11. Поміняти місцями 1-й і 3-й рядки в матриці .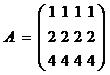

Розв’язування:

>> A=[1 1 1 1;2 2 2 2;4 4 4 4]

А =

1 1 1 1

2 2 2 2

4 4 4 4

>> A=[А(3:);A(2:);A(1:)]

А =

4 4 4 4

2 2 2 2

1 1 1 1

Приклад 3.12. Помножити елементи другого рядка матриці А з попереднього приклада на число 2.

Розв’язування:

>> A=[1 1 1 1;2 2 2 2;4 4 4 4];

>> A=[А(1:);A(2:)*2;A(3:)]

А =

1 1 1 1

4 4 4 4

4 4 4 4

Приклад 3.13. Обчислити добуток матриць .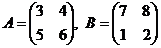

Розв’язування:

>> A=[3 4;5 6];B=[7 8;1 2];

>> A*B

ans =

25 32

41 52

>> B*A

ans =

61 76

13 16

Приклад 3.14. Виконати поелементне множення матриць А і В з прикладу 3.13.

>> A=[3 4;5 6];B=[7 8;1 2];

А.*B

ans =

21 32

5 12

>> times (A,B)

ans =

21 32

5 12

Приклад 3.15. Обчислити визначник матриці ,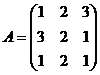

мінор М₁₂ та алгебраїчне доповнення А₁₂.

Розв’язування:

>> A=[1 2 3; 3 2 1;1 2 1]

А =

1 2 3

3 2 1

1 2 1

>> det(A)

ans =

>> M12=det([А(2:3,1),A(2:3,3)])

M12 =

>> A12=(-1)^(1+2)*M12

 

A12 =

-2

Приклад 3.16. Перевірити властивості визначника.

Розв’язування:

>> A=[2 4;6 4];isequal (det(A),det(A'))

ans =

>> A=[2 4;6 4];isequal (det(A),

-det([А(:,2),A(:,1)]))

ans =

>> A=[2 4;6 4];isequal (4*det([2 1;6 1]),det(A))

ans =

>> A=[1,2,3;1,2,3;2,3,4];isequal (det(A),0)

ans =

>> A=[1,2,3;1,2,5;1,2,4];isequal (det(A),0)

ans =

>> A=[2 4;6 4];

>> isequal (det(A),det([А(:,1),A(:,2)+2*A(:,1)]))

ans =

>> A=[2 4 6;

0 4 2;0 0 1];isequal (det(A),8)

ans =

Приклад 3.17. Визначити, чи є матриця 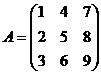невиродженою.

Розв’язування:

>> A=[1 4 7;2 5 8;3 6 9]

А =

1 4 7

2 5 8

3 6 9

>> det(A)

ans =

Приклад 3.18. Обчислити обернену матрицю матриці .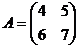

Розв’язування:

>> A=[4 5;6 7]

А =

4 5

6 7

>> inv(A)

ans =

-3.5000 2.5000

3.0000 -2.0000

Приклад 3.19. Обчислити ранг матриці А з прикладу 3.17.

Розв’язування:

>> A=[1 4 7;2 5 8;3 6 9]; rank(A)

ans =

Приклад 3.20. Перевірити властивості рангу матриці, використовуючи матрицю А з прикладу 3.17.

Розв’язування:

>> A=[1 4 7;2 5 8;3 6 9]

А =

1 4 7

2 5 8

3 6 9

>> isequal(rank(A),rank(A'))

ans =

>> isequal(rank(A),rank([А(3:);A(2:);A(1:)]))

ans =

>> isequal(rank(A),rank([А(:,1),2*A(:,2),A(:,3)]))

ans =

>> isequal(rank(A),rank([А(:,1),A(:,1)+A(:,2),A(:,3)]))

ans =

Таким чином, всі розглянуті властивості для рангу матриці виконуються.

Приклад 3.21. Перевірити рівність матриць 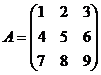і 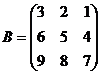, а також чи є вони еквівалентними.

Розв’язування:

>> A=[1 2 3;4 5 6;7 8 9],B=[3 2 1;6 5 4;9 8 7]

А =

1 2 3

4 5 6

7 8 9

B =

3 2 1

6 5 4

9 8 7

>> isequal(A,B)

ans =

>> isequal(rank(A),rank(B))

ans =

Отже, матриці А і В не рівні між собою, але є еквівалентними.

Приклад. 3.22. Дослідити на сумісність наступну систему рівнянь:

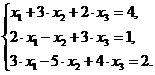
Розв’язування:

>> A=[1 3 2;2 -1 3;3 -5 4];B=[4 1 2]';

>> [rank(A),rank([А B])]

ans =

2 3

Оскільки ранг розширеної матриці не дорівнює рангу матриці коефіцієнтів системи лінійних рівнянь, то дана система несумісна, тобто не має розв’язку.

Приклад 3.23. Розв’язати за допомогою матричного методу систему лінійних рівнянь:

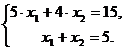
Розв’язування:

1. Обчислимо визначник матриці А: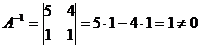

2. Оскільки визначник матриці А не дорівнює нулю, то існує обернена матриця А ':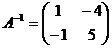

3. Обчислимо добуток оберненої матриці на вектор-стовпець вільних членів: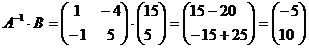

4. Отриманий результат і є вектор-стовпец X: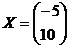

Для розв’язування системи лінійних рівнянь за матричним методом за допомогою MATLAB в командне вікно слід ввести наступну команду:

>> X=inv([5 4;1 1])*[15;5]

X =

-5

Приклад 3.24. Розв’язати систему лінійних рівнянь за допомогою формул Крамера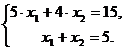

Розв’язування:

1. Обчислимо визначник системи А, і якщо він не дорівнює нулю, обчислимо визначники А_х1 і А_х2: , , .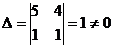

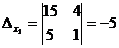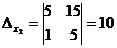2. Застосуємо формули Крамера для визначення значень х₁ і х₂: , .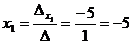

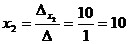3. Таким чином, розв’язком системи є х1 = -5, х2 = 10.

Виконаємо вказані операції за допомогою системи MATLAB:

>> A=[5 4;1 1];B=[15;5];d=det(A)

d =

>> [B А(:,2)],dx1=det(ans) % обчислення визначника dx1

ans =

15 4

5 1

dx1 =

-5

>> [А(:,1) B],dx2=det(ans) % обчислення визначника dx2

ans =

5 15

1 5

dx2 =

>> X=[dx1/d;dx2/d] % отримання розв’язку системи

X =

-5

Приклад 3.25. Розв’язати систему лінійних рівнянь з прикладу 3.25 з використанням оператора «\» в системі MATLAB:

>> A=[1 -2 2;2 -1 3;3 2 -1],B=[3;9;4]

А =

1 -2 2

2 -1 3

3 2 -1

B =

X=(A\B)'

X =

1.0000 2.0000 3.0000

Інструкція до виконання лабораторної роботи №3