Запишемо параметричну задачу такого виду в загальній формі:
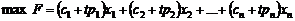 (5)
(5)
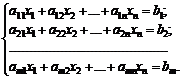 (6)
(6)

 . (7)
. (7)
За деякого фіксованого значення  задача (5)—(7) перетворюється в звичайну задачу лінійного програмування. Зміни коефіцієнтів цільової функції в процесі реалізації симплексного методу впливатимуть на значення оцінкового ряду (
задача (5)—(7) перетворюється в звичайну задачу лінійного програмування. Зміни коефіцієнтів цільової функції в процесі реалізації симплексного методу впливатимуть на значення оцінкового ряду (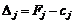 ).
).
Для оптимального плану задачі лінійного програмування в постановці (1)—(3), як відомо, оцінки векторів розраховують так:
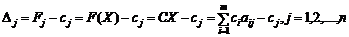 .
.
Якщо цільова функція має вигляд (5), то оцінки векторів розраховуватимуться за формулою:
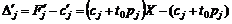

Позначимо перетворені методом повних виключень Жордана—Гаусса в процесі перерахунку початкової симплексної таблиці  через
через 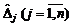 , аналогічно
, аналогічно  — як
— як 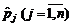 . Остання симплексна таблиця набуде такого вигляду:
. Остання симплексна таблиця набуде такого вигляду:
Таблиця1.
| і | Базис | С баз | План | с 1 + t 0 p 1 | ... | cm + t 0 pm | ... | cn + t 0 pn |
| x 1 | ... | xm | ... | xn | ||||
| x 1 | с 1 + t 0 p 1 | 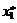
| a 11 | ... | 
| ... | 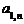
| |
| x 2 | с 2 + t 0 p 2 | 
| a 21 | ... | 
| ... | 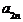
| |
| … | … | … | … | … | … | … | … | … |
| m | xm | cm + t 0 pm | 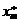
| am 1 | ... | 
| ... | 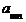
|
| m + 1 | 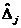
| 
| 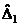
| 
| 
| |||
| m + 2 | 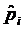
| 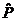
| 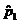
| ... | 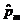
| ... | 
| |
| m + 3 | Fj – cj ³ 0 | 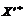
| 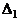 
| ... |  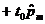
| ... |  
|
Таблиця (аналогічно випадку параметричної зміни вектора обмежень —табл.1) містить два додаткових рядки, що дає змогу стежити за перетвореннями величин  після кожної ітерації.
після кожної ітерації.
 2018-01-21
2018-01-21 439
439








