Тема заняття: Розв’язання взаємо-двоїстих задач.
Мета: сформувати вміння й навички побудови та розв’язання двоїстих задач.
Методичні рекомендації: Вивчити лекцію №3 та ознайомиться з наступною літературою [1 с. 118-155], [3 с. 80-126], [4 с. 88-116].
Постановка завдання:
Кожній задачі лінійного програмування відповідає двоїста, що формується за допомогою певних правил безпосередньо з умови прямої задачі.
Якщо пряма задача лінійного програмування має вигляд
Z = c 1 x 1 + c 2 x 2 + … + cnxn ® max
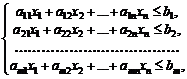
 ,
,
то двоїста задача записується так:
F = b 1 y 1 + b 2 y 2 + … + bmym ® min
за обмежень

 .
.
Порівнюючи ці дві сформульовані задачі, доходимо висновку, що двоїста задача лінійного програмування утворюється з прямої задачі за такими правилами.
1. Кожному обмеженню прямої задачі відповідає змінна двоїстої задачі. Кількість невідомих двоїстої задачі дорівнює кількості обмежень прямої задачі.
2. Кожній змінній прямої задачі відповідає обмеження двоїстої задачі, причому кількість обмежень дорівнює кількості невідомих прямої задачі.
3. Якщо цільова функція прямої задачі задається на пошук найбільшого значення (max), то цільова функція двоїстої задачі — на визначення найменшого значення (min), і навпаки.
4. Коефіцієнтами при змінних в цільовій функції двоїстої задачі є вільні члени системи обмежень прямої задачі.
5. Правими частинами системи обмежень двоїстої задачі є
коефіцієнти при змінних в цільовій функції прямої задачі.
6. Матриця
 ,
,
що складається з коефіцієнтів при змінних у системі обмежень прямої задачі, і матриця коефіцієнтів в системі обмежень двоїстої задачі

утворюються одна з одної транспонуванням, тобто заміною рядків стовпчиками, а стовпчиків — рядками.
Двоїсті пари задач лінійного програмування бувають симетричні та несиметричні.
У симетричних задачах обмеження прямої та двоїстої задач є нерівностями, а змінні обох задач можуть набувати лише невід’ємних значень.
У несиметричних задачах обмеження прямої задачі можуть бути записані як рівняння, а двоїстої — лише як нерівності.
У цьому разі відповідні змінні двоїстої задачі набувають будь-якого значення, не обмеженого знаком.
Різні можливі форми прямих задач лінійного програмуван-
ня та відповідні їм варіанти моделей двоїстих задач наведено далі.
| Пряма задача | Двоїста задача |
| Симетричні | |

| 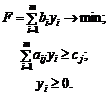
|

| 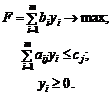
|
Несиметричні

| 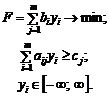
|

| 
|
Розглянемо застосування теорії та співвідношень двоїстості на конкретному прикладі.
| Приклад 1 |
До наведеної далі задачі лінійного програмування записати двоїсту задачу. Розв’язати одну з них симплекс-методом та визначити оптимальний план іншої задачі.
Z = –5 x 1 + 2 x 2 ® max;
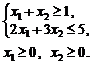
Розв’язування. Перш ніж записати двоїсту задачу, необхідно пряму задачу звести до відповідного вигляду. Оскільки цільова функція Z максимізується і в системі обмежень є нерівності, то вони повинні мати знак «≤». Тому перше обмеження моделі помножимо на (–1). При цьому знак нерівності зміниться на протилежний. Отримаємо:
Z = –5 x 1 + 2 x 2 ® max;

Тепер за відповідними правилами складемо двоїсту задачу:
F = – y 1 + 5 y 2 ® min;


Оскільки записані задачі симетричні, будь-яку з них можна розв’язати симплекс-методом. Наприклад, визначимо спочатку оптимальний план прямої задачі. Для цього застосуємо алгоритм симплекс-методу.
1. max (–5 x 1 + 2 x 2 + 0 x 3 + 0 x 4);
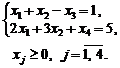
2. Векторна форма запису системи обмежень має вигляд
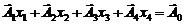 ,
,
де 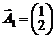 ,
, 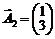 ,
,  ,
,  ,
, 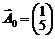 .
.
У системі векторів для утворення початкового одиничного базису відсутній вектор 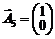 . Тому використаємо штучну змінну в першому обмеженні.
. Тому використаємо штучну змінну в першому обмеженні.
3. Розширена задача лінійного програмування буде така:
max (–5 x 1 + 2 x 2 + 0 x 3 + 0 x 4 – Мx 5);
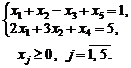
У цій задачі х 4 та х 5 — базисні змінні, а х 1, х 2, х 3 — вільні.
Нехай х 1 = х 2 = х 3 = 0, тоді х 4 = 5; х 5 = 1.
Перший опорний план задачі:
х 0 = (0; 0; 0; 5; 1), Z 0 = – M.
4. Подальше розв’язування прямої задачі подано у вигляді симплекс-таблиці:
| Базис | С баз | План | –5 | М | q | |||
| x1 | x2 | x3 | x4 | x5 | ||||
 x 5 x 4 x 5 x 4
| – М 0 | 1 5 | 1 2 | 1 3 | –1 0 | 0 1 | 1 0 | 1 5/3 |
| Zj – Cj ³ 0 | 0 – М | 5 –М | –2 –М | 0 М | 0 0 | 0 0 | ||
 x 2 x 4 x 2 x 4
| 2 0 | 1 2 | 1 –1 | 1 0 | –1 3 | 0 1 | 1 –3 | — 2/3 |
| Zj – Cj ³ 0 | –2 | 2 + М | ||||||
| x 2 x 3 | 2 0 | 5/3 2/3 | 2/3 –1/3 | 1 0 | 0 1 | 1/3 1/3 | 0 –1 | |
| Zj – Cj ³ 0 | 10/3 | 19/3 | 2/3 | 0 + М |
З останньої симплекс-таблиці бачимо, що оптимальний план прямої задачі
Х * = (0; 5/3; 2/3; 0), Z max = 10/3.
Згідно зі співвідношенням двоїстості за першою теоремою можна записати, що оптимальний план двоїстої задачі існує і
min F = max Z = 10/3,
 ,
,
де  та міститься в стовпчику «C баз» останньої симплекс-таблиці;
та міститься в стовпчику «C баз» останньої симплекс-таблиці;
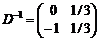
він також міститься в останній симплекс-таблиці у стовпчиках змінних «x 5» та «x 4», які утворювали початковий базис.
Отже,
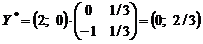 ,
,
min F = –1 × 0 + 5 × 2/3 = 10/3.
Застосовуючи до розв’язування прямої задачі симплекс-метод, ми знайшли її оптимальний план, а потім визначили оптималь-
ний розв’язок двоїстої задачі за допомогою співвідношень першої теореми двоїстості.
Розв’язати задачі лінійного програмування симплекс-методом та знайти рішення прямої та двоїстої задачі. До наведених задач записати двоїсту задачу до поставленої задачі лінійного програмування. Розв’язати одну з пари задач і за цим розв’язком визначити оптимальний план іншої задачі.
Розв’язати задачі лінійного програмування симплекс-методом та знайти рішення прямої та двоїстої задачі. До наведених задач записати двоїсту задачу до поставленої задачі лінійного програмування. Розв’язати одну з пари задач і за цим розв’язком визначити оптимальний план іншої задачі.
Задача 1
 ,
,
Задача 2
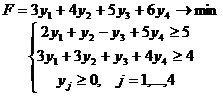 ,
,
Задача 3
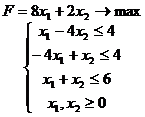 .
.
ДОДАТКОВІ ЗАВДАННЯ:
Розв’язати задачі лінійного програмування симплекс-методом та знайти рішення прямої та двоїстої задачі. До наведених задач записати двоїсту задачу до поставленої задачі лінійного програмування. Розв’язати одну з пари задач і за цим розв’язком визначити оптимальний план іншої задачі.
Задача 4

Задача 5
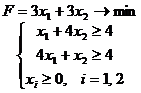
 2018-01-21
2018-01-21 393
393








