В этой лекции речь будет идти только о квадратных матрицах.
Каждой квадратной матрице можно поставить в соответствие некоторое число – определитель этой матрицы. Прежде чем дать общее определение, введем определители матриц 2х2 и 3х3.
2.1. Определитель матрицы 2х2.
Назовем определителем матрицы

число, равное  .
.
Обозначения:
 ,
,  ,
,  .
.
Пример:
 .
.
2.2. Определитель матрицы 3х3. Для квадратной матрицы 3-го порядка определитель задается следующим образом:
 .
.
Раскрывая входящие в это выражение определители второго порядка, получаем:
 .
.
Несмотря на громоздкость выражения, запомнить его легко.
Тройные произведения элементов матрицы на первой схеме берутся со знаком «+», на второй – со знаком «-.».
2.3. Перестановки и подстановки.
Прежде чем обобщить понятие определителя на матрицы более высокого порядка, дадим некоторые новые определения..
Рассмотрим конечное множество из  элементов. Занумеруем эти элементы первыми числами натурального ряда. Таким образом, будем считать, что элементами являются числа 1, 2, ….
элементов. Занумеруем эти элементы первыми числами натурального ряда. Таким образом, будем считать, что элементами являются числа 1, 2, ….  .
.
Обычный порядок этих чисел можно изменить, переставив их. Например, числа 1,2,3 можно расположить так: 3,1,2 или 2,3,1. Всякое расположение чисел 1,2,…,  назовем перестановкой.
назовем перестановкой.
Утверждение. Число всех перестановок множества из  элементов равно
элементов равно  !.
!.
Доказательство. Общий вид перестановки таков:
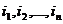 ,
,
где каждое из  - одно из чисел
- одно из чисел  , причем все они различны. В качестве
, причем все они различны. В качестве  можно взять любое из
можно взять любое из  чисел. Для каждого выбора числа
чисел. Для каждого выбора числа  есть
есть 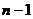 возможность выбрать
возможность выбрать  . Если
. Если  и
и  выбраны, то остается
выбраны, то остается 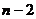 возможности выбрать
возможности выбрать  , и т.д. Итак, получаем
, и т.д. Итак, получаем
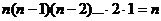 !
!
способов переставить числа 1,2,….  . Ч.т.д.
. Ч.т.д.
Подстановкой будем называть любое взаимно однозначное отображение множества  на себя. Чтобы это лучше представить, запишем одну под другой две строки: в первой запишем элементы множества
на себя. Чтобы это лучше представить, запишем одну под другой две строки: в первой запишем элементы множества  , а во второй – любую перестановку этих элементов. Получим
, а во второй – любую перестановку этих элементов. Получим

И будем считать, что при этой подстановке элемент 1 переходит в  , элемент 2 – в
, элемент 2 – в  и т.д. Очевидно, что каждой подстановке соответствует перестановка, и это соответствие взаимно однозначное, поэтому мы можем записывать подстановку, указывая только перестановку в нижней строке. Множество всех подстановок обозначим
и т.д. Очевидно, что каждой подстановке соответствует перестановка, и это соответствие взаимно однозначное, поэтому мы можем записывать подстановку, указывая только перестановку в нижней строке. Множество всех подстановок обозначим  . Подстановки будем обозначать греческими буквами
. Подстановки будем обозначать греческими буквами  ; запись
; запись  означает, что подстановка
означает, что подстановка  отображает элемент
отображает элемент  в элемент
в элемент  .
.
2.4. Четность подстановки.
Пусть
 -
-
некоторая перестановка. Говорят, что  и
и  образуют инверсию, если
образуют инверсию, если 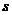 <
<  , но
, но  >
>  . Перестановка называется четной, если она содержит четное число инверсий, и нечетной, если число инверсий нечетно. Например:
. Перестановка называется четной, если она содержит четное число инверсий, и нечетной, если число инверсий нечетно. Например:
2 3 1 5 4 - 3 инверсии (2,1), (3,1).(5,4); перестановка нечетная.
4 3 1 5 2 - 6 инверсий (4,3), (4,1), (4,2), (3,1), (3,2), (5,2); перестановка четная.
Установленное выше соответствие между перестановками и подстановками позволяет говорить и о четности подстановок: будем называть подстановку четной (нечетной), если соответствующая ей перестановка четная (нечетная). Знак подстановки  равен +1, если подстановка четная, и -1, если подстановка нечетная.
равен +1, если подстановка четная, и -1, если подстановка нечетная.
Лемма. Две перестановки
 и
и 
имеют различную четность.
Доказательство. Пусть сначала  , т.е. вторая получается из первой перестановкой двух соседних элементов:
, т.е. вторая получается из первой перестановкой двух соседних элементов:
 ;
;  .
.
Инверсии, содержащиеся в первой перестановке, в которых хотя бы один элемент не равен  или
или  сохраняются и во второй перестановке. Исключение составляет пара
сохраняются и во второй перестановке. Исключение составляет пара  . Если она образует инверсию, тово второй перестановке пара
. Если она образует инверсию, тово второй перестановке пара 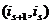 инверсии не образует. И наоборот, если инверсии не было, то во второй перестановке, поменявшись местами, эти элементы образуют инверсию. Значит, количество инверсий в этих перестановках отличается на одну инверсию.
инверсии не образует. И наоборот, если инверсии не было, то во второй перестановке, поменявшись местами, эти элементы образуют инверсию. Значит, количество инверсий в этих перестановках отличается на одну инверсию.
Пусть теперь 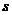 и
и  произвольные. Тогда вторую перестановку можно получить из первой за несколько шагов, каждый раз меняя соседние элементы:
произвольные. Тогда вторую перестановку можно получить из первой за несколько шагов, каждый раз меняя соседние элементы:
 и
и  ,
,  и
и  ,…,
,…,  и
и  - всего
- всего  шагов;
шагов;
затем  и
и  ,
,  и
и  ,…,
,…,  и
и  - всего
- всего  шагов.
шагов.
Итого, мы сделаем  шагов. На каждом шаге знак перестановки менялся, а поскольку число шагов было нечетно, то знаки перестановок различны.
шагов. На каждом шаге знак перестановки менялся, а поскольку число шагов было нечетно, то знаки перестановок различны.
2.5. Определитель произвольного порядка.
Теперь можно ввести понятие определителя  - го порядка.
- го порядка.
Пусть  – квадратная матрица
– квадратная матрица  х
х  . Определителем матрицы
. Определителем матрицы  называется число, равное следующему выражению:
называется число, равное следующему выражению:
 (*)
(*)
В выражение для определителя входит  ! слагаемых, каждое из которых соответствует некоторой подстановке
! слагаемых, каждое из которых соответствует некоторой подстановке  . Знак перед слагаемым зависит от четности подстановки. Каждое слагаемое является произведением
. Знак перед слагаемым зависит от четности подстановки. Каждое слагаемое является произведением  сомножителей: по одному из каждой строки и из каждого столбца.
сомножителей: по одному из каждой строки и из каждого столбца.
Проверим согласованность с формулой (*) формул для вычисления определителей в случаях  и
и  .
.
А).  = 2. Имеем 2 перестановки: 1,2 и 2,1. Первая четная, вторая нечетная.
= 2. Имеем 2 перестановки: 1,2 и 2,1. Первая четная, вторая нечетная.


Б).  = 3. Имеем 3! = 6 перестановок:
= 3. Имеем 3! = 6 перестановок:
перестановка четность
1 2 3 +
1 3 2 -
2 1 3 -
2 3 1 +
3 1 2 +
3 2 1 -
 .
.
Сопоставьте это с формулой, приведенной ранее.
2.6. Свойства определителя.
1). Если в матрице  одна из строк нулевая (или один из столбцов нулевой), то
одна из строк нулевая (или один из столбцов нулевой), то  . Доказательство очевидно, ведь в этом случае каждое слагаемое в формуле (*) равно 0.
. Доказательство очевидно, ведь в этом случае каждое слагаемое в формуле (*) равно 0.
2). Если две строки матрицы поменять местами (элементарное преобразование типа I), то определитель матрицы поменяет знак (кососимметричность). Иначе, пусть

Тогда  .
.
Доказательство. Рассмотрим произвольное слагаемое в формуле (*) для матрицы  , соответствующее подстановке
, соответствующее подстановке  , пока не учитывая его знак. Это слагаемое встретится и в разложении определителя
, пока не учитывая его знак. Это слагаемое встретится и в разложении определителя  , но будет соответствовать другой подстановке
, но будет соответствовать другой подстановке
 :
: 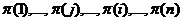 .
.
Согласно лемме четность подстановок  и
и  различна, а значит, различны и знаки, с которыми эти слагаемые входят в соответствующие разложения определителей. Итак, при переходе от
различна, а значит, различны и знаки, с которыми эти слагаемые входят в соответствующие разложения определителей. Итак, при переходе от  к
к  все слагаемые в разложении (*) поменяют знаки, следовательно, изменит знак и определитель.
все слагаемые в разложении (*) поменяют знаки, следовательно, изменит знак и определитель.
3). Если в матрице  две одинаковые строки, то ее определитель равен нулю.
две одинаковые строки, то ее определитель равен нулю.
Доказательство моментально следует из предыдущего свойства. Если в такой матрице поменять местами две одинаковые строки, то определитель должен изменить знак. С другой стороны, он не изменится, так как не изменится и сама матрица. Значит, определитель равен нулю.
4). Пусть одна из строк матрицы представлена как сумма двух строк, т.е. матрица имеет вид
 .
.
Тогда  , где
, где
 ,
,  .
.
Докажем это. По формуле (*)

 =
=
 +
+ 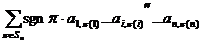
 .
.
5). Если одну из строк матрицы умножить на некоторое число  , то определитель умножится на это же число
, то определитель умножится на это же число  . Действительно, если все элементы одной строки умножить на
. Действительно, если все элементы одной строки умножить на  , то умножится на
, то умножится на  и каждое слагаемое в формуле (*), а значит, и определитель матрицы.
и каждое слагаемое в формуле (*), а значит, и определитель матрицы.
6). Если к одной строке матрицы прибавить другую строку, умноженную на какое-нибудь число (элементарное преобразование типа II), то определитель матрицы не изменится. Доказательство немедленно следует из предыдущих свойств. Пусть

 .
.
Тогда  , где
, где
 -
-
матрица, у которой  -я и
-я и  -я строки совпадают, и следовательно, ее определитель равен нулю. Значит,
-я строки совпадают, и следовательно, ее определитель равен нулю. Значит,  .
.
7). При транспонировании матрицы определитель не меняется:
Докажем это. В разложении определителя (*) любое слагаемое с точностью до знака является произведением элементов матрицы по одному из каждой строки и из каждого столбца. Поэтому с точностью до знаков слагаемые в разложениях определителей исходной и транспонированной матриц совпадают. Теперь разберемся со знаками.
Возьмем произвольное слагаемое из разложения определителя матрицы  и покажем, что в разложение определителя транспонированной матрицы оно будет входить с тем же знаком. Пусть это слагаемое соответствует подстановке π:
и покажем, что в разложение определителя транспонированной матрицы оно будет входить с тем же знаком. Пусть это слагаемое соответствует подстановке π:  . Упорядочим сомножители по второму индексу, т.е. по столбцам:
. Упорядочим сомножители по второму индексу, т.е. по столбцам:  , где
, где  – некоторая другая подстановка, причем
– некоторая другая подстановка, причем  . Заметим, что количество инверсий в перестановках
. Заметим, что количество инверсий в перестановках  и
и 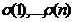 совпадает, ведь если выполнялось условие
совпадает, ведь если выполнялось условие  <
<  , но
, но 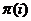 >
>  , то после упорядочивания сомножителей по номерам столбцов появится соответствующая инверсия в перестановке номеров строк. Значит, четность подстановок
, то после упорядочивания сомножителей по номерам столбцов появится соответствующая инверсия в перестановке номеров строк. Значит, четность подстановок  и
и  совпадает.
совпадает.
8). Из предыдущего свойства следует, что свойства 1)-6) справедливы не только для строк матрицы, но и для столбцов.
2.7. Разложение определителя по первой строке.
Заметим, что с увеличением размеров матрицы, т.е. с ростом  , количество слагаемых в разложении (*) растет с огромной скоростью. При
, количество слагаемых в разложении (*) растет с огромной скоростью. При  =4 оно равно 24, при
=4 оно равно 24, при  =5 - 120, а при
=5 - 120, а при  =6 - уже 720! Очевидно, что формула (*) едва ли пригодна для вычисления определителя при
=6 - уже 720! Очевидно, что формула (*) едва ли пригодна для вычисления определителя при  >3.
>3.
Выведем формулу, позволяющую свести вычисление определителя порядка  к вычислению нескольких определителей порядка
к вычислению нескольких определителей порядка 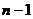 .
.
Сначала дадим
Определение. Минором  называется определитель матрицы, получившейся из исходной вычеркиванием
называется определитель матрицы, получившейся из исходной вычеркиванием  -й строки и
-й строки и  -го столбца.
-го столбца.
Теперь сформулируем и докажем следующую теорему.
Теорема 1 (о разложении определителя по первой строке). Справедлива формула:
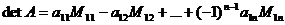 . (**)
. (**)
Доказательство. Рассмотрим разложение (*). Разобьем сумму на группы слагаемых следующим образом: сначала соберем те произведения, которые содержат  , потом те, которые содержат
, потом те, которые содержат  и т.д. Получим
и т.д. Получим


Заметим, что если есть перестановка 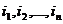 , то
, то  - перестановка чисел от 1 до
- перестановка чисел от 1 до  без числа
без числа  . Число инверсий во второй перестановке на
. Число инверсий во второй перестановке на  меньше чем в первой: так как число
меньше чем в первой: так как число  стояло на первом месте, то после него находилось
стояло на первом месте, то после него находилось  чисел, меньших
чисел, меньших  . После того, как
. После того, как  убрали, эти инверсии исчезли. Остальные инверсии остались, новые появиться не могли.
убрали, эти инверсии исчезли. Остальные инверсии остались, новые появиться не могли.
Рассмотрим какую-нибудь группу слагаемых:
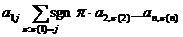
Все произведения элементов входят в разложение минора  , но знак, с которым они входят в это разложение – в силу сделанного выше замечания – отличается на множитель
, но знак, с которым они входят в это разложение – в силу сделанного выше замечания – отличается на множитель  . Таким образом, получаем требуемую формулу.
. Таким образом, получаем требуемую формулу.
Дадим еще одно определение.
Определение. Число  называется алгебраическим дополнением элемента
называется алгебраическим дополнением элемента  . Тогда формула (**) примет более изящный вид:
. Тогда формула (**) примет более изящный вид:
 .
.
2.8. Разложение определителя по произвольной строке.
Теорема 2. Справедлива формула
 (***)
(***)
для любого  .
.
Доказательство. Вычислим определитель следующим образом: сначала поставим  -ю строку на 1-е место, сохранив при этом порядок остальных строк, а затем воспользуемся утверждением теоремы 1.
-ю строку на 1-е место, сохранив при этом порядок остальных строк, а затем воспользуемся утверждением теоремы 1.
Для того, чтобы  -ю строку поставить на 1-е место, сохранив при этом порядок остальных строк, нужно будет
-ю строку поставить на 1-е место, сохранив при этом порядок остальных строк, нужно будет  раз поменять местами соседние строки: сначала
раз поменять местами соседние строки: сначала  -ю и (
-ю и ( )-ю, затем (
)-ю, затем ( )-ю и (
)-ю и ( )-ю и т.д. Получится матрица
)-ю и т.д. Получится матрица

Заметим, что  (через
(через 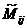 обозначим минор получившейся матрицы
обозначим минор получившейся матрицы  ). Теперь вычислим определитель.
). Теперь вычислим определитель.

Теорема доказана.
2.9. Разложение определителя по столбцу. Разложить определитель можно не только по произвольной строке, но и по произвольному столбцу:
 .
.
Доказательство становится очевидным, если вспомнить, что определитель матрицы не меняется при транспонировании.
2.9. Вычисление определителей.
Формула (***), на первый взгляд, не выглядит более простой, чем (*). Но на самом деле это не так. Пусть нам нужно вычислить определитель матрицы
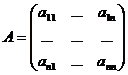
и пусть, к примеру, 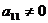 . С помощью элементарных преобразований типа II можно привести матрицу к виду
. С помощью элементарных преобразований типа II можно привести матрицу к виду
 ,
,
Причем  . (Вспомните, как приводится матрица к треугольному виду.) Разложим определитель по первому столбцу – от суммы в формуле (***) останется одно слагаемое, - и вычисление определителя порядка
. (Вспомните, как приводится матрица к треугольному виду.) Разложим определитель по первому столбцу – от суммы в формуле (***) останется одно слагаемое, - и вычисление определителя порядка  сведется к вычислению определителя порядка
сведется к вычислению определителя порядка 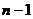 . Повторив эту процедуру необходимое количество раз, придем к нужному результату.
. Повторив эту процедуру необходимое количество раз, придем к нужному результату.
2.10. Некоторые замечания.
1.  .
.
2. 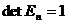 .
.
Доказательства этих утверждений очевидны.
3. Менее тривиальным является утверждение, которое примем без доказательства:
 .
.
4. Если в формуле (***) вместо алгебраических дополнений  взять алгебраические дополнения элементов другой строки, то выражение станет равным нулю:
взять алгебраические дополнения элементов другой строки, то выражение станет равным нулю:
 если
если  .
.
Это утверждение станет очевидным, если заметить, что левая часть является разложением определителя

который равен нулю, так как две его строки совпадают.
 2018-01-21
2018-01-21 984
984






