Процеси теплопровідності, які постійно відбуваються в навколишньому середовищі, привертали до себе увагу вчених на протязі всієї історії розвитку людства. Найпростішою математичною моделлю такого процесу є диференціальне рівняння теплопровідності параболічного типу

з відповідною початковою умовою та крайовими умовами.
Потреби практики приводили до різного узагальнення даного рівняння (перехід до квазілінійності та нелінійності, перехід до кусково-однорідних коефіцієнтів, перехід до нових ортогональних криволінійних систем координат; перехід до диференціальних рівнянь параболічного типу вищих порядків та ін.) В усіх випадках процеси теплопровідності вивчалися в припущенні, що межа середовища жорстка по відношенню до відбиття хвиль. Різко змінюється картина розповсюдження тепла, якщо межа середовища є м’якою по відношенню до відбиття хвиль. Математично це означає наявність в крайових операторах та диференціальних операторах спряження похідної стосовно часової змінної.
В другій половині ХХ-го століття дуже поширений метод кусково-сталих коефіцієнтів, що проводив до диференціальних рівнянь із сингулярними коефіцієнтами типу дельта-функції та її похідних. Та одержати інтегральне зображення точного аналітичного розв’язку таких задач неможливо. Ці труднощі можна обійти, якщо здійснити моделювання процесів поширення тепла методом гібридних диференціальних операторів.
Дана робота присвячена моделюванню нестаціонарних процесів теплопровідності методом гібридного диференціального оператора Лежандра – (Бесселя, Фур’є) в припущенні, що межа середовища м’яка по відношенню до відбиття хвиль.
Перший та другий параграф присвячені моделювання процесу теплопровідності в неоднорідному середовищі з м’якими межами методом гібридного диференціального оператора Лежандра – Бесселя - Фур’є та Лежандра - Фур’є – Бесселя на полярній осі відповідно. Третій та четвертий параграф присвячені моделювання процесів теплопровідності в неоднорідних середовищах з м’якими межами методом гібридного диференціального оператора Лежандра - Фур’є– Бесселя та Лежандра– Бесселя - Фур’є на полярній осі  відповідно. У п’ятому параграфі подані основні вимоги з охорони праці.
відповідно. У п’ятому параграфі подані основні вимоги з охорони праці.
Розглянемо детальніше перший параграф, який називається «Моделювання процесу теплопровiдностi в неоднорідному середовищі з м'якими межами методом гібридного диференціального оператора Лежандра - Бесселя - Фур'є на полярнiй осi».
Розглянемо задачу про побудову обмеженого в області  розв’язку сепаратної системи диференціальних рівнянь теплопровідності параболічного типу:
розв’язку сепаратної системи диференціальних рівнянь теплопровідності параболічного типу:
 (1)
(1)
за початковими умовами
 (2)
(2)
та умовами спряження
 (3)
(3)
У рівностях беруть участь диференціальні оператори Лежандра  , Бесселя
, Бесселя  та Фур’є
та Фур’є 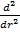 , а також узагальнені диференціальні оператори спряження
, а також узагальнені диференціальні оператори спряження
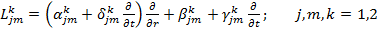 .
.
Розв’язок задачі (1)-(3) одержимо методом інтегрального перетворення Лапласа стосовно t в припущенні, що шукані та задані функції є зображення за Лапласом стосовно змінної t ( ).
).
У зображенні за Лапласом отримуємо крайову задачу: побудувати обмежений на множині  розв’язок сепаратної системи звичайних диференціальних рівнянь Лежандра, Бесселя та Фур’є для модифікованих функцій
розв’язок сепаратної системи звичайних диференціальних рівнянь Лежандра, Бесселя та Фур’є для модифікованих функцій
 (4)
(4)
за умовами спряження
 (5)
(5)
Фундаментальну систем у розв’язків для диференціальногорівняння Лежандра  складають узагальненіприєднані функції Лежандра першого роду
складають узагальненіприєднані функції Лежандра першого роду 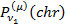 та другого роду
та другого роду  ; фундаментальну систему розв’язків для диференціальногорівняння Бесселя
; фундаментальну систему розв’язків для диференціальногорівняння Бесселя  складають функції Бесселя уявного аргументу першого роду
складають функції Бесселя уявного аргументу першого роду  та другого роду
та другого роду  ; фундаментальну систему розв’язків для диференціального рівняння Фур’є
; фундаментальну систему розв’язків для диференціального рівняння Фур’є  складають функцiї
складають функцiї  і
і  .
.
Нявнiсть фундаментальної системи розв’язків дозволяє побудувати розв’язоккрайової задачі (4), (5)методом функційКоші:
 (9)
(9)
У рівностях (9) беруть участь функції Коші  , які знаходимо використавши їх властивості:
, які знаходимо використавши їх властивості:
 , (10)
, (10)

Функції Коші мають вигляд:



Залишилося знайти величини A1,A2,B2,B3. Для їх знаходження використаємо умови спряження (5), що дають алгебраїчну неоднорідну систему із чотирьох рівнянь, яку розв’язуємо за правилом Крамера:
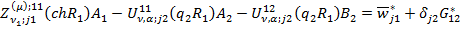 (21)
(21)

Далі визначаємо головні розв’язки крайової задачі (4), (5), а саме функції Гріна породжені неоднорідністю умов спряження, функції впливупороджені неоднорідністю системи (4).
У результаті однозначної розв’язності крайової задачі (4), (5), підстановки визначених величин 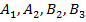 у рівності (9) та повернувшись до оригіналу одержуємо єдиний розв’язок вихідної параболічної задачі (1)-(3):
у рівності (9) та повернувшись до оригіналу одержуємо єдиний розв’язок вихідної параболічної задачі (1)-(3):

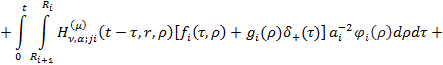




де 

Як результат можна сформулювати таку теорему:
Теорема: Якщо  є оригіналом за Лапласом,
є оригіналом за Лапласом,  – двічі неперервно диференційовні за змінною r та задовольняють однорідні умови спряження, то параболічна задача має розв’язок
– двічі неперервно диференційовні за змінною r та задовольняють однорідні умови спряження, то параболічна задача має розв’язок  а при виконанні умови однозначної розв’язності крайової задачі він єдиний.
а при виконанні умови однозначної розв’язності крайової задачі він єдиний.
Особливими точками функції Гріна  та функції впливу
та функції впливу  є точки галуження
є точки галуження 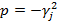 та
та 
 . Покладемо
. Покладемо  Одержимо:
Одержимо:  Якщо
Якщо  то при
то при  маємо:
маємо:  Використавши методу контурного інтегралу в поєднанні з лемою Жордана й теоремою Коші перейдемо до розрахункових формул:
Використавши методу контурного інтегралу в поєднанні з лемою Жордана й теоремою Коші перейдемо до розрахункових формул:
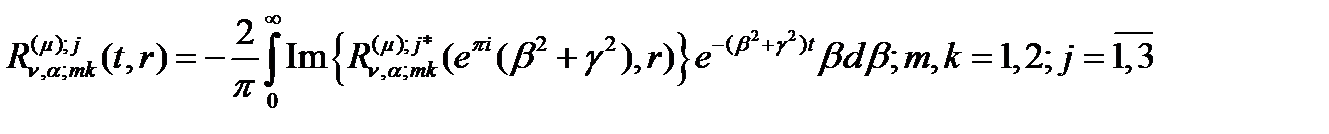
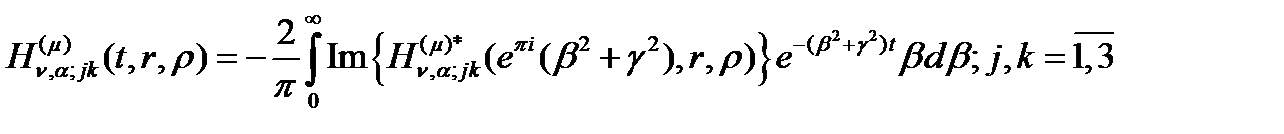
 2018-01-21
2018-01-21 196
196






