Кафедра «Теория вероятностей и математическая статистика»
Вопросы и задачи
По теории вероятностей
Для студентов
бакалавриата экономики
МОСКВА 2010 ГОД
ВГОБУ ВПО «ФИНАНСОВЫЙ УНИВЕРСИТЕТ
ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ»
Кафедра «Теория вероятностей и математическая статистика»
УТВЕРЖДАЮ
Ректор Финуниверситета
____________М.А. Эскиндаров
«____» ______________2010 г.
Вопросы и задачи
По теории вероятностей
Для студентов бакалавриата экономики
Одобрено кафедрой
«Математика и финансовые приложения»
(протокол №3 от 6 октября 2010 г.)
МОСКВА 2010 ГОД
УДК
ББК
Браилов А.В., Гончаренко В.М., Зададаев С.А., Коннов В.В. Вопросы и задачи по теории вероятностей. Для студентов бакалавриата экономики. М.: Финансовый университет при Правительстве РФ, кафедра «Теория вероятностей и математическая статистика», 2010. — 44 с.
Рецензент: Мелехина Т.Л., доцент кафедры «Теория вероятностей и математическая статистика».
Пособие содержит теоретические вопросы и практические задания по курсу «Теория вероятностей и математическая статистика», читаемому в третьем семестре студентам бакалавриата экономики. Предназначено для организации самостоятельной работы студентов и для подготовки к экзамену, а также содержит основные требования к уровню освоения дисциплины в части теории вероятностей.
Под редакцией С.А.Зададаева.
Браилов Андрей Владимирович
Гончаренко Василий Михайлович
Зададаев Сергей Алексеевич
Коннов Валерий Владимирович
Компьютерный набор, верстка: Браилов А.В., Зададаев.С.А.
Формат 60x90/16. Гарнитура Таймс.
Усл. 3,125 п.л. Изд. №______2010.
Тираж 20 экз. Заказ № ______________
Отпечатано в Финансовом университете при Правительстве РФ
125468, Ленинградский пр-т, 49
Полное или частичное воспроизведение или размножение каким-либо способом настоящего издания допускается только с письменного разрешения Финансовой академии при Правительстве РФ.
© Финансовый университет при Правительстве РФ, 2010.
Содержание
I. Теоретические вопросы
1. Случайные события ……………………………………………………… …… 4
2.Схема Бернулли ………………………………………………………………... 7
3. Дискретные случайные величины ……………………………………… …… 9
4. Непрерывные случайные величины …………………………………………. 13
5. Начальные и центральные моменты случайных величин ………………….. 15
6. Случайные векторы …………………………………………………………… 16
7. Предельные теоремы теории вероятностей ……………………………. …… 18
II. Практические задания
1. Случайные события …………………………………………………………… 20
2. Дискретные случайные величины …………………………………………… 26
3. Непрерывные случайные величины …………………………………………. 32
4. Случайные векторы …………………………………………………………… 36
Дополнения ………………………………...……………………………………… 42
Ответы к задачам ………………………………………………………………… 43
I. ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ
Случайные события
● Основные определения и свойства. Алгебра событий
1. Что называется случайным событием, связанным с опытом? Как определятся событие, противоположное данному? Приведите примеры.
2. Что называется суммой и произведением событий  и
и  ? Имеют ли смысл сумма и произведение событий, относящихся к разным опытам? Перечислите все случаи наступления события
? Имеют ли смысл сумма и произведение событий, относящихся к разным опытам? Перечислите все случаи наступления события  .
.
3. Что называется пространством элементарных событий? Что называется случайным событием? Какие исходы называются благоприятными для события  ? Что называется вероятностью события
? Что называется вероятностью события  ? Приведите примеры. Можно ли в опыте с бросанием игральной кости считать элементарными следующие события:
? Приведите примеры. Можно ли в опыте с бросанием игральной кости считать элементарными следующие события:  – выпадение числа очков, меньших
– выпадение числа очков, меньших  ;
; 
 – выпадение более
– выпадение более  очков?
очков?
4. Какие события называются достоверными и невозможными и каковы их вероятности? Пусть  ,
,  и
и  – случайные события. Перечислите все случаи наступления события
– случайные события. Перечислите все случаи наступления события 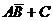 .
.
5. В каком случае событие  называют следствием события
называют следствием события  ? Какие события называются равными? Объясните, почему
? Какие события называются равными? Объясните, почему 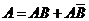 .
.
6. Пусть  и
и  – случайные события. Упростите выражение
– случайные события. Упростите выражение 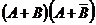 . Найдите событие, противоположное событию
. Найдите событие, противоположное событию 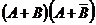 ?
?
7. Докажите, что  . Что означает событие
. Что означает событие  ?
?
8. Докажите, что 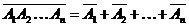 . Что означает событие
. Что означает событие  ?
?
9. Сформулируйте статистическое определение вероятности. Почему вероятность удовлетворяет условию 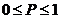 ? Возможны ли случаи
? Возможны ли случаи  и
и  ? Ответ обоснуйте.
? Ответ обоснуйте.
● Теорема сложения вероятностей
10. Сформулируйте и докажите теорему сложения вероятностей для любых событий  и
и  . Что такое правило сложения вероятностей для несовместных событий
. Что такое правило сложения вероятностей для несовместных событий  и
и  ?
?
11. Какие события  называются попарно несовместными? Сформулируйте правило сложения вероятностей для попарно несовместных событий
называются попарно несовместными? Сформулируйте правило сложения вероятностей для попарно несовместных событий  . Приведите пример попарно несовместных событий
. Приведите пример попарно несовместных событий  и
и  таких что
таких что 
12. Объясните, почему  для событий
для событий  и
и  . Чему равна сумма
. Чему равна сумма 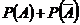 вероятностей противоположных событий? Ответ обоснуйте.
вероятностей противоположных событий? Ответ обоснуйте.
13. Верно ли, что если событие  является следствием события
является следствием события  , то
, то 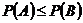 ? Ответ обоснуйте.
? Ответ обоснуйте.
● Условная вероятность
14. Дайте определение условной вероятности 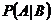 и приведите его статистическую интерпретацию. Укажите примеры, когда: 1)
и приведите его статистическую интерпретацию. Укажите примеры, когда: 1)  ; 2)
; 2) 
● Независимые события и правило умножения вероятностей
15. Какие события называются независимыми? Докажите, что если события  и
и  независимы, то независимы события
независимы, то независимы события  и
и  .
.
16. Что такое правило умножения вероятностей: а) для независимых событий  и
и  ; б) для любых
; б) для любых  и
и  ? Запишите правило умножения вероятностей для трех (зависимых) событий
? Запишите правило умножения вероятностей для трех (зависимых) событий  и
и  . Приведите примеры применения соответствующих формул.
. Приведите примеры применения соответствующих формул.
17. Как определяется независимость в случае трех событий? Рассмотрите пример: пусть в опыте с бросанием двух монет события  означают:
означают:  – на первой монете выпал герб;
– на первой монете выпал герб;  – на второй монете выпал герб;
– на второй монете выпал герб;  – обе монеты упали на одну сторону. Будут ли независимы все три события? Почему?
– обе монеты упали на одну сторону. Будут ли независимы все три события? Почему?
18. Как соотносятся понятия независимые события  и
и  и несовместные события
и несовместные события  и
и  ? Следует ли из независимости событий
? Следует ли из независимости событий  и
и  независимость событий
независимость событий  и
и  ? Почему?
? Почему?
19. События  и
и  независимы; события
независимы; события  и
и  также независимы. При этом события
также независимы. При этом события  и
и 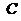 несовместны. Следует ли из этого, что события
несовместны. Следует ли из этого, что события  и
и  независимы? Ответ необходимо обосновать.
независимы? Ответ необходимо обосновать.
20. События  и
и  независимы; события
независимы; события  и
и  также независимы. При этом события
также независимы. При этом события  и
и 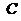 несовместны. Следует ли из этого, что события
несовместны. Следует ли из этого, что события  и
и 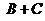 независимы? Ответ необходимо обосновать.
независимы? Ответ необходимо обосновать.
21. Как определяется независимость событий  в случае
в случае  ? Является ли равенство
? Является ли равенство  достаточным для независимости событий
достаточным для независимости событий  ? Ответ обоснуйте.
? Ответ обоснуйте.
22. Имеется две игральные кости: одна – симметричная, вторая – несимметричная. Пусть 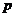 – вероятность того, что при одновременном броске данных костей на них выпадет одинаковое число очков. Докажите, что
– вероятность того, что при одновременном броске данных костей на них выпадет одинаковое число очков. Докажите, что 
● Геометрический подход к определению вероятности
23. В чем состоит геометрический подход к определению вероятности. Как находится вероятность попадания в заданное множество, если точка случайно выбирается на отрезке  в треугольнике
в треугольнике 
24. В чем состоит геометрический подход к определению вероятности. Как находится вероятность попадания в заданное множество, если точка случайно выбирается в круге радиуса  ? в кубе со стороной
? в кубе со стороной 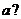
● Полная группа событий. Формула полной вероятности и формула Байеса
25. Что такое полная группа событий? Приведите пример, когда события  ,
, 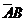 и
и  не образуют полной группы событий.
не образуют полной группы событий.
26. Верно ли, что события  ,
,  ,
,  и
и  образуют полную группу для любых событий
образуют полную группу для любых событий  и
и  ? Ответ обоснуйте.
? Ответ обоснуйте.
27. Событие  влечет событие
влечет событие 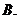 Верно ли, что
Верно ли, что  Дайте обоснованный ответ.
Дайте обоснованный ответ.
28. Сформулируйте и докажите формулу полной вероятности. Приведите пример ее применения.
29. Сформулируйте и докажите формулу Байеса. Приведите пример ее применения.
Схема Бернулли
● Вероятности 
30. В чем состоит схема Бернулли? Запишите формулу  для вероятности
для вероятности 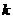 успехов в серии
успехов в серии  испытаний по схеме Бернулли и приведите пример ее применения.
испытаний по схеме Бернулли и приведите пример ее применения.
31. Выведите формулу  для вероятности
для вероятности 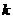 успехов в серии
успехов в серии  испытаний по схеме Бернулли.
испытаний по схеме Бернулли.
● Наиболее вероятное число успехов
32. Выведите формулу для наиболее вероятного числа успехов в серии  испытаний по схеме Бернулли.
испытаний по схеме Бернулли.
33. Пусть  – вероятность
– вероятность 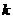 успехов в серии
успехов в серии  независимых испытаний с вероятностью успеха
независимых испытаний с вероятностью успеха 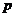 в каждом испытании. При каком
в каждом испытании. При каком 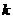 вероятность
вероятность  достигает максимума? Совпадает ли это число с математическим ожиданием количества успехов? Чему равна сумма
достигает максимума? Совпадает ли это число с математическим ожиданием количества успехов? Чему равна сумма  ?
?
34. Может ли наиболее вероятное число успехов в схеме Бернулли отличаться от математического ожидания числа успехов на 2? Ответ обоснуйте.
● Вероятности  при больших значениях
при больших значениях 
35. Запишите локальную приближенную формулу Лапласа, приведите основные свойства функции Гаусса  и укажите ее график. При каких условиях данная формула дает хорошее приближение? Какие условия применимости отличают эту формулу от приближенной формулы Пуассона?
и укажите ее график. При каких условиях данная формула дает хорошее приближение? Какие условия применимости отличают эту формулу от приближенной формулы Пуассона?
36. Запишите интегральную приближенную формулу Лапласа и приведите основные свойства функции Лапласа  . При каких условиях данная формула дает хорошее приближение?
. При каких условиях данная формула дает хорошее приближение?
37. Укажите выражение для функции Лапласа  . Докажите нечетность функции
. Докажите нечетность функции  и нарисуйте график
и нарисуйте график  . Чему равно
. Чему равно  ?
?
38. Используя интегральную приближенную формулу Лапласа, выведите формулу для оценки отклонения относительной частоты события  от вероятности
от вероятности 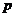 наступления
наступления  в одном опыте.
в одном опыте.
● Предельная теорема Пуассона
39. Сформулируйте и докажите предельную теорему Пуассона.
40. Запишите приближенные формулы Пуассона. При каких условиях они дают хорошее приближение? Приведите пример их применения.
Дискретные случайные величины
● Функция распределения случайной величины
41. Что такое случайная величина? Что такое дискретная случайная величина? Что называется функцией распределения случайной величины? Приведите пример функции  , которая является функцией распределения некоторой дискретной случайной величины
, которая является функцией распределения некоторой дискретной случайной величины 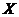 , объясните, почему это так и постройте ее график.
, объясните, почему это так и постройте ее график.
42. Сформулируйте основные свойства функции распределения случайной величины и продемонстрируйте их на примере.
43. Может ли график функции распределения быть прямой линией? Ответ обоснуйте.
44. Что такое дискретная случайная величина? Может ли таблица
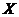
| 
| 
| 
|

| 
| 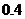
| 
|
рассматриваться как закон распределения дискретной случайной величины?
45. Дана дискретная случайная величина с законом распределения
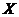
| 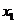
| 
| 
| 
|

| 
| 
| 
| 
|
Что является ее функцией распределения  ? Постройте график
? Постройте график  и опишите его точки разрыва. Как вычисляется вероятность
и опишите его точки разрыва. Как вычисляется вероятность  ?
?
● Типичные законы распределения дискретных случайных величин
46. Что называется геометрическим распределением с параметром 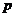 ? Приведите пример опытов, в котором определена случайная величина, распределенная по геометрическому закону с параметром
? Приведите пример опытов, в котором определена случайная величина, распределенная по геометрическому закону с параметром 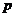 .
.
47. Что называется биномиальным распределением с параметрами  и
и 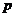 ? Приведите пример опытов, в котором определена случайная величина, распределенная по биномиальному закону.
? Приведите пример опытов, в котором определена случайная величина, распределенная по биномиальному закону.
48. Какой закон распределения называется законом Пуассона? В чем состоит связь этого закона с предельной теоремой Пуассона (приближенной формулой Пуассона)?
● Независимые дискретные случайные величины
49. Как определяется независимость случайных величин? Игральную кость бросают  раз. Пусть
раз. Пусть 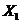 – число выпадений грани
– число выпадений грани 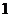 ;
;  – число выпадений грани
– число выпадений грани  . Будут ли зависимыми случайные величины
. Будут ли зависимыми случайные величины 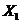 и
и  ? Ответ обоснуйте.
? Ответ обоснуйте.
50. Пусть  – независимые случайные величины, принимающие с вероятностью
– независимые случайные величины, принимающие с вероятностью  значения 0 и 1. Верно ли, что
значения 0 и 1. Верно ли, что  и
и 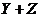 – независимые случайные величины? Ответ обоснуйте.
– независимые случайные величины? Ответ обоснуйте.
● Математическое ожидание и дисперсия дискретной случайной величины
51. Дайте определение математического ожидания дискретной случайной величины. Поясните его смысл на примере случайной величины с двумя возможными значениями, исходя из статистического определения вероятности.
52. Перечислите основные свойства математического ожидания дискретной случайной величины. Объясните, что понимается под суммой и произведением случайных величин?
53. Приведите (с обоснованием) пример дискретного распределения вероятностей, для которого не существует математическое ожидание.
54. Может ли математическое ожидание дискретной случайной величины, принимающей целые значения, быть числом нецелым? Ответ обоснуйте.
55. Пусть 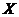 – дискретная случайная величина, принимающая только неотрицательные значения и имеющая математическое ожидание
– дискретная случайная величина, принимающая только неотрицательные значения и имеющая математическое ожидание  . Докажите, что
. Докажите, что  .
.
56. Докажите, что если 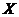 и
и  – независимые дискретные случайные величины, принимающие конечное множество значений, то
– независимые дискретные случайные величины, принимающие конечное множество значений, то  .
.
57. Докажите, что если 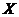 и
и  – дискретные случайные величины, принимающие конечное множество значений, то
– дискретные случайные величины, принимающие конечное множество значений, то  .
.
58. Как определяется и что характеризует дисперсия дискретной случайной величины 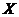 ? Перечислите основные свойства дисперсии.
? Перечислите основные свойства дисперсии.
59. Докажите, что если 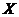 – дискретная случайная величина, то
– дискретная случайная величина, то  .
.
60. Пусть 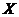 – дискретная случайная величина. Может ли выполняться неравенство
– дискретная случайная величина. Может ли выполняться неравенство 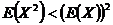 ? Ответ обоснуйте.
? Ответ обоснуйте.
61. Докажите, что если 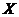 и
и  – независимые случайные величины, то
– независимые случайные величины, то  .
.
62. Пусть 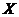 – дискретная случайная величина, распределенная по биномиальному закону с параметрами
– дискретная случайная величина, распределенная по биномиальному закону с параметрами  и
и 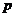 . Докажите, что
. Докажите, что  .
.
63. Докажите, что для биномиальной случайной величины с вероятностью успеха 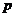 в каждом из
в каждом из  независимых испытаний выполняется равенство
независимых испытаний выполняется равенство  .
.
64. Пусть 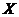 – дискретная случайная величина, распределенная по закону Пуассона с параметром
– дискретная случайная величина, распределенная по закону Пуассона с параметром  Докажите, что
Докажите, что 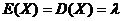 .
.
65. Пусть 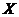 – дискретная случайная величина, распределенная по геометрическому закону с параметром
– дискретная случайная величина, распределенная по геометрическому закону с параметром  Докажите, что
Докажите, что 
66. Пусть 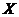 – дискретная случайная величина, распределенная по геометрическому закону с параметром
– дискретная случайная величина, распределенная по геометрическому закону с параметром  Докажите, что
Докажите, что 
● Ковариация и коэффициент корреляции
67. Как определяется ковариация Cov  случайных величин
случайных величин 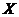 и
и  ? Докажите, что
? Докажите, что  Cov
Cov 
68. Сформулируйте основные свойства ковариации Cov  случайных величин
случайных величин 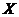 и
и  . Докажите, что Cov
. Докажите, что Cov  .
.
69. Как определяется коэффициент корреляции  случайных величин
случайных величин 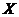 и
и  ? Каковы основные свойства коэффициента корреляции? Что можно сказать о
? Каковы основные свойства коэффициента корреляции? Что можно сказать о 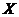 и
и  , если
, если 
70. Докажите, что коэффициент корреляции  случайных величин
случайных величин 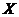 и
и  удовлетворяет условию
удовлетворяет условию 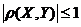 . Что можно сказать о
. Что можно сказать о 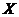 и
и  , если
, если 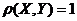 ? Если
? Если 
71. Чему равен  и Cov
и Cov  при условии независимости случайных величин
при условии независимости случайных величин  ? Что можно сказать о
? Что можно сказать о  , если
, если  , где
, где 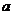 и
и 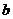 – некоторые числа
– некоторые числа  ? Ответ обоснуйте.
? Ответ обоснуйте.
 2018-01-21
2018-01-21 598
598







