2018-01-21
1124
| Номера точек | 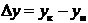 , м
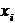|  , м
|  , м
|  , м
| 
| 
|  , м
| 
|
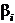
| 4257, 50 4358,30 |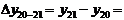 
=4358,304257,50=
=+100,80
| 2590,40 2594,40 | 
=2594,402590,40=
=+4,00
| 
=100,80/4,00=
=25,200
| 
| 
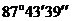
=100,88
|
| |
| А | 4257,50 4308,80 |  +51,30
| 2590,40 2630,4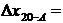0 |  +40,00
| 1,283 |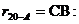 
| 65,05 | =354016 |
| А | 4358,30 4308,80 |  49,50
| 2594,40 2590,40 |  +36,00
| 1,375 | 
| 49,52 | 
=381758
|
| 4256,10 4367,80 |  +111,70
| 3016,60 3012,10 |  4,50
| 24,822 | 111,79 |
 ...
| ||
| В | 4256,10 ... |  ...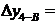
| 3016,60 ... |  ...
| ||||
| В | 4367,80 ... |  ...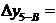
| 3012,10 ... |  ...
|  ..
|
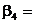Тогда тангенс румба линии 20 A равен
,
где 
, 
координаты конечной точки линии (в данном случае координаты точки А); 
, 
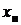координаты начальной точки линии (№ 20).
Подставляя исходные данные, получим
.
По знакам приращений координат 
и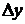 
(плюс в числителе и знаменателе) определяем наименование румба линии 20 А: северо-восток. По таблицам приложения находим величину румба 520323, следовательно, 
СВ 520323.
Для определения угла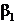 
необходимо знать также румб линии 20 21. Пусть в результате аналогичных вычислений получено: 
СВ: 874339. Тогда 
874339 520323 = 354016 (см. рис. 74).
Горизонтальное проложение линий 20 A вычисляется по формулам
; 
; 
.
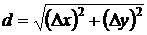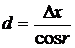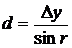В данном случае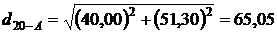 
м.
Контроль: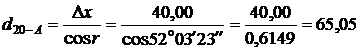 
м.
Результаты вычислений представляются в табличном виде (см. табл. 11).
| Рис. 73 | Рис. 74 |
Контролем угловых вычислений является равенство 180 суммы внутренних углов треугольников 20 А 21 и 4 В 5 (см. рис. 72), причем значения углов могут быть определены по значениям румбов соответствующих сторон. Так, например, для первого треугольника внутренний угол
520353 + 535823 = 1060146.
Тогда сумма внутренних углов треугольника равна
354016 + 1060146 + 381758 = 1800000.
