Тема 2. Плоскость в пространстве

Занятия 6-7. Прямые и плоскости

Тема 1. Прямая на плоскости

1. Составить уравнение прямой, состоящей из точек, равноудаленных от точек и .

2. Дан треугольник , , , 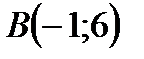. Составить уравнения прямых, содержащих медиану 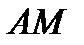, биссектрису 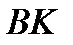, высоту , серединный перпендикуляр к стороне .

3. Найти координаты проекции точки 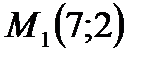на прямую 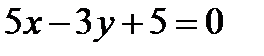, а также координаты точки, симметричной точке относительно данной прямой.

4. Доказать, что прямые и пересекаются, найти их точку пересечения и косинус острого угла между ними.

5. Доказать, что прямые и 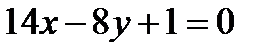параллельны, и найти расстояние между ними.

6. В прямоугольном треугольнике с гипотенузой известны координаты вершин и , а вершина лежит на прямой . Найти координаты вершины . Указание: задача имеет два решения.

7. В равнобедренном треугольнике с основанием 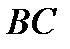известны координаты вершин и , а вершина 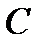лежит на прямой . Найти координаты вершины . Указание: задача имеет два решения.

Тема 2. Плоскость в пространстве

1. Составить уравнение плоскости, параллельной плоскости и проходящей через точку . Найти расстояние между этими плоскостями.

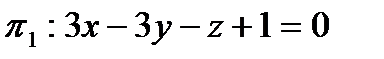2. Составить уравнение плоскости, проходящей через точку и перпендикулярной плоскостям и .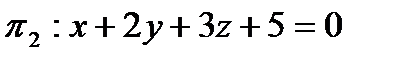

3. Дан тетраэдр , , , , 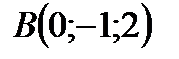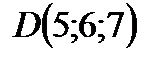. Составить уравнение плоскости 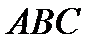основания тетраэдра и найти его высоту, опущенную из вершины .

4. Доказать, что плоскости 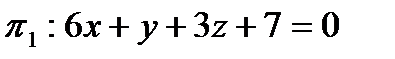и пересекаются, и найти косинус острого угла между ними.

5. Найти расстояние от начала координат до плоскости .

6. Найти объем пирамиды, ограниченной координатными плоскостями и плоскостью .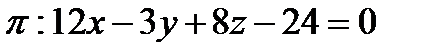

7. Найти значение 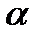, при котором расстояние от точки 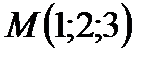до плоскости равно 3. Указание: задача имеет два решения.

8. Составить уравнение плоскости, параллельной плоскости 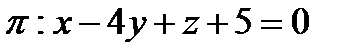и отстоящей от точки на расстояние . Указание: задача имеет два решения.

9. Составить уравнения плоскостей, делящих пополам двугранные углы, образованные плоскостями и .

10. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей и параллельно вектору 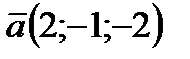. Указание: использовать пучок плоскостей.

11. На оси найти точки, равноудаленные от точки и плоскости . Указание: задача имеет два решения.