Расчет общих сопротивлений
Для простых комбинаций резисторов применяется прямое использование формул для последовательных и параллельных соединений проводников.

Для смешанных соединений, если есть возможность, применяется расчет сопротивлений набора последовательных и параллельных участков.
 Пользуясь правилами расчета последовательного и параллельного соединения, можно рассчитать сопротивление сложной цепи, содержащей резисторы, соединенные различными комбинированными способами. Один из методов такого расчета – шаговый (рекуррентный). Его удобно применять в том случае, когда схема состоит из повторяющихся элементов (резисторов). Шаговый метод основан на том, что результат первого действия (шага) используется во втором, второй – в третьем и т.д. Число шагов зависит от числа повторяющихся структурных элементов.
Пользуясь правилами расчета последовательного и параллельного соединения, можно рассчитать сопротивление сложной цепи, содержащей резисторы, соединенные различными комбинированными способами. Один из методов такого расчета – шаговый (рекуррентный). Его удобно применять в том случае, когда схема состоит из повторяющихся элементов (резисторов). Шаговый метод основан на том, что результат первого действия (шага) используется во втором, второй – в третьем и т.д. Число шагов зависит от числа повторяющихся структурных элементов.
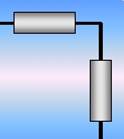
Подчеркнем, что вид соединения определяется порядком протекания электрического тока, а не тем как элементы расположены в том или ином приборе, и тем более не тем, как они изображены на схеме. Так два резистора, показанные на рисунке соединены последовательно, а не перпендикулярно!
Рассчитаем сопротивление цепи, изображенной на рисунке.
 Для упрощения расчетов и экономии места положим, что сопротивления всех резисторов одинаковы и равны R.
Для упрощения расчетов и экономии места положим, что сопротивления всех резисторов одинаковы и равны R.
Будем шаг за шагом упрощать схему, заменяя ее части эквивалентными сопротивлениями. Резисторы R2 и R3 соединены параллельно, поэтому их общее сопротивление равно R23 = R/2;
 резисторы R1 и R23 соединены последовательно, следовательно, их сопротивление
резисторы R1 и R23 соединены последовательно, следовательно, их сопротивление

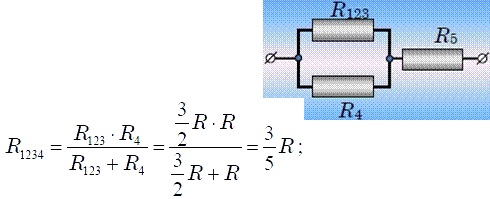
для расчета параллельно соединенных резисторов R123 и R4 воспользуемся формулой
 наконец, этот резистор последовательно соединен с резистором R5, поэтому, общее сопротивление исходной цепи равно:
наконец, этот резистор последовательно соединен с резистором R5, поэтому, общее сопротивление исходной цепи равно:

 2017-10-25
2017-10-25 438
438







