Основные положения теории

Лабораторная работа №12

 

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЦЕПЯХ

 

Цель работы

1. Экспериментальное подтверждение свойств и режимных параметров линейных цепей при наличии в них переходных процессов.

2. Овладение экспериментальными методами исследования параметров цепей на характер протекания в них переходных процессов.

Основные положения теории

Процесс перехода режима работы электрической цепи от одного к другому называется переходным. В общем случае в электротехнике принято, что возникновение переходного процесса связано с явлением коммутации. Принимается допущение, что коммутация начинается в момент времени t = 0 и совершается мгновенно: . При этом различают два момента времени: момент времени непосредственно предшествующий коммутации t (−0), или t (0−) и момент времени непосредственно после коммутации t (0+), или t (+0). Предположение приводит к законам коммутации.

В момент коммутации ток в ветви с индуктивностью не изменяется, т. е. i . Напряжение на емкости в момент коммутации не изменяется, т. е. .

Значения и называются независимыми начальными условиями. Для идеальных элементов R, C ток в момент коммутации может меняться скачком, т.е. 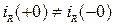; 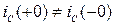. Для идеальных элементов R и L в момент коммутации скачком могут меняться напряжения, т.е. ; . Значения ; ; ; 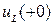называются зависимыми начальными условиями.

В переходном процесса мгновенные значения напряжений и токов не являются периодическими функциями времени. Если положительные направления напряжения и тока на элементе одинаковы, то уравнения идеальных элементов имеют вид:

, , .

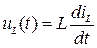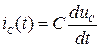Переходный процесс в цепи с одним реактивным элементом и источником постоянного напряжения (тока) описывают линейным неоднородным (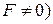 дифференциальным уравнением вида

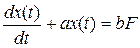
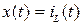В этом уравнение для R – C цепи, для R–L цепи. F – постоянная, зависящая от величин напряжения или тока источников, a и b не зависящие от времени коэффициенты.

Общее решение этого уравнения имеет вид 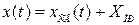. Свободная составляющая решения определяется как общее решение однородного дифференциального уравнения.

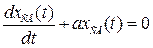
и имеет вид: . Здесь: А – постоянная интегрирования; 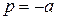корень характеристического уравнения . Величина имеет размерность времени и называется постоянной времени. За интервал времени свободная составляющая решения уменьшается в раз. Выражение позволяет оценить длительность переходного процесса. Можно принять от 4τ до 5τ.

Величина 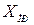является частным решением уравнения

Величина 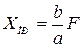не зависит от времени и может быть рассчитана в установившемся режиме после коммутации. Общее решение приобретает вид . Постоянная интегрирования А определяется из независимых начальных условий. При t =0 и .