2.1. Основные уравнения четырехполюсника
Связь между входными и выходными напряжениями и токами 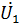 и
и 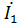 ;
; 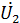
и 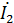 линейного пассивного четырехполюсники (при положительных направлениях напряжений и токов, указанных на рис.1) может быть выражена одной из следующих шести форм основных уравнений:
линейного пассивного четырехполюсники (при положительных направлениях напряжений и токов, указанных на рис.1) может быть выражена одной из следующих шести форм основных уравнений:
Форма 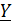 :
:
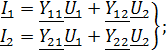 (1)
(1)
Форма 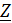 :
:
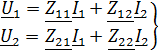 ; (2)
; (2)
Форма 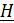 :
:
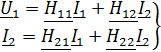 ; (3)
; (3)
Форма 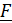 :
:
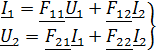 ; (4)
; (4)
Форма 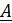 :
:
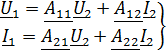 ; (5)
; (5)
Форма 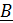 :
:
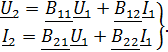 (6)
(6)
Вместо коэффициентов 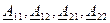 используется часто их запись в виде
используется часто их запись в виде 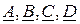 .
.

Рис.1. Пассивный четырехполюсник
При выбранных положительных направлениях напряжений и токов, согласно рис. 1, при нагрузке четырехполюсника со стороны вторичных зажимов на сопротивление 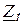 , последнее связано с выходным напряжением и током соотношением:
, последнее связано с выходным напряжением и током соотношением:
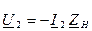 . (7)
. (7)
Коэффициенты основных уравнений четырехполюсника (1) – (6) называются параметрами четырехполюсника. Они определяются только схемой самого четырехполюсника. В общем случае все коэффициенты четырехполюсника комплексны.
2.2. Способы определения коэффициентов четырехполюсники
Коэффициенты четырехполюсника могут быть определены различными способами:
1) составлением уравнений по законам Кирхгофа (либо методом контурных токов или узловых потенциалов) и представлением их решения в виде одной из форм уравнений (1) – (6);
2) по значениям напряжений и токов в режимах холостого хода и короткого замыкания (см. формулы (8) – (13);
3) разбивкой сложного четырехполюсника на более простые четырехполюсники, параметры которых известны;
4) способом эквивалентных преобразований (например, путем преобразования треугольника сопротивлений в эквивалентную звезду).
Коэффициенты четырехполюсника могут быть определены по известным напряжениям и токам в режимах холостого хода и короткого замыкания по формулам, которые получаются из формул (1) – (6):
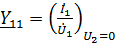 ;
; 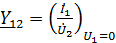 ;
;
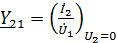 ;
; 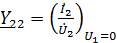 . (8)
. (8)
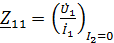 ;
; 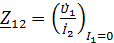 ;
;
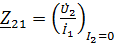 ;
; 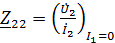 . (9)
. (9)
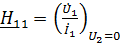 ;
; 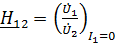 ;
;
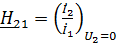 ;
; 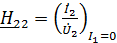 . (10)
. (10)
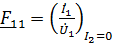 ;
; 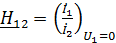 ;
;
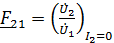 ;
; 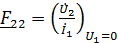 . (11)
. (11)
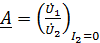 ;
; 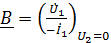 ;
;
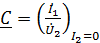 ;
; 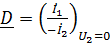 . (12)
. (12)
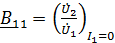 ;
; 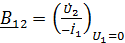 ;
;
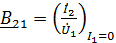 ;
; 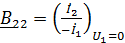 . (13)
. (13)
2.3. Виды соединения четырехполюсников
Несколько четырехполюсников могут быть соединены между собой различными способами: параллельно, последовательно, последовательно-параллельно, параллельно-последовательно а также каскадно (в виде цепочки). На рис.2 Приведен пример каскадного соединения двух четырехполюсников, коэффициенты которых выражены в форме 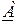 . При этом матричное уравнение параметров полученного сложного четырехполюсника будет иметь вид:
. При этом матричное уравнение параметров полученного сложного четырехполюсника будет иметь вид:
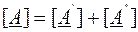 ,
,
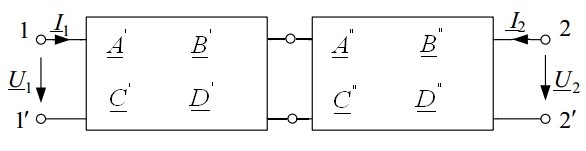
Рис.2. Каскадное соединение четырехполюсников
Откуда следует матричная форма записи основных уравнений четырехполюсника:

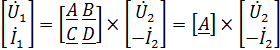 .
.
Аналогичные формулы справедливы при соединении любого числа четырехполюсников.
Следует иметь в виду, что указанные формулы нахождения матриц сложных четырехполюсников справедливы лишь при выполнении условий регулярности их соединения Соединение четырехполюсника регулярно в случае, когда токи, протекающие через оба первичных зажима каждого их четырехполюсников, равны по величине и обратны по направлению.
2.4. Характеристические параметры четырехполюсника
Помимо параметров, указанных в п.2.1., применяются характеристические параметры четырехполюсника: характеристические сопротивления 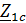 ,
, 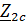 , и характеристическая постоянная передачи
, и характеристическая постоянная передачи 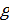 , которые также полностью характеризуют четырехполюсник.
, которые также полностью характеризуют четырехполюсник.
Характеристическими называются два сопротивления 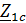 и
и 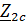 , обладающие следующим свойством: входное сопротивление четырехполюсника со стороны зажимов 1–1’ при подключении к зажимам 2–2’ сопротивления
, обладающие следующим свойством: входное сопротивление четырехполюсника со стороны зажимов 1–1’ при подключении к зажимам 2–2’ сопротивления 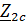 , равно
, равно 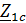 , и наоборот, при подключении к зажимам 1–1’ сопротивления
, и наоборот, при подключении к зажимам 1–1’ сопротивления 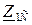 входное сопротивление четырехполюсника со стороны зажимов 2-2’ равно
входное сопротивление четырехполюсника со стороны зажимов 2-2’ равно 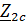 .
.
Режим работы четырехполюсника, нагруженного соответствующим характеристическим сопротивлением, называется согласованным.
Постоянная передачи:
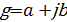 (14)
(14)
где 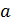 – характеристическое (собственное) затухание, Hп или dB, b – характеристический (собственный) коэффициент фазы, рад или град.
– характеристическое (собственное) затухание, Hп или dB, b – характеристический (собственный) коэффициент фазы, рад или град.
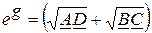 . (15)
. (15)
Для вычисления g согласно (15), следует вычислить комплекс
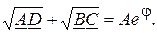
представив его в показательной форме. С учетом (14), (15) получаем
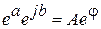 (16)
(16)
откуда 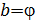 ;
; 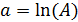 , Нп.
, Нп.
Характеристические параметры можно определить через параметры формы 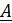 :
:
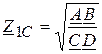 ,
, 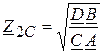 . (17)
. (17)
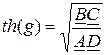 ,
, 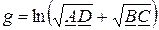 (18)
(18)
и наоборот коэффициенты формы 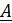 могут быть выражены через характеристические параметры:
могут быть выражены через характеристические параметры:


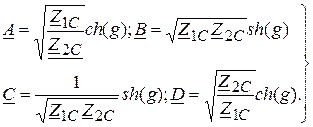 (19)
(19)
2.5. Согласованный режим работы четырехполюсника
В этом случае связь между комплексами токов и напряжений на входе и выходе задается соотношениями:
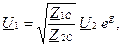
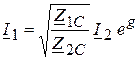 , (20)
, (20)
а для модулей действующих значений
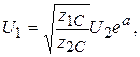
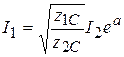 . (21)
. (21)
все входящие в формулу (21) величины чисто вещественные.
Для симметричных четырехполюсников 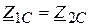 , поэтому выражение (21) перепишется в виде:
, поэтому выражение (21) перепишется в виде:
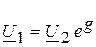 ,
, 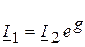 . (23)
. (23)
Обозначив 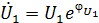 ,
, 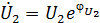 ,
, 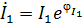 ,
, 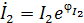 ,
, 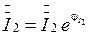 на основе (23), получим:
на основе (23), получим:
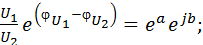
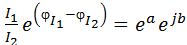
откуда для симметричного четырехполюсника
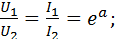
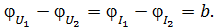 (24)
(24)
Выражения (24) раскрывают физический смысл коэффициентов a и b; величина 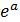 показывает, во сколько раз величины тока и напряжения на выходе четырехполюсника меньше, чем соответствующие значения на входе, т.е. во сколько раз затухает сигнал, проходя через четырехполюсник, работающий в согласованном режиме. Коэффициент фазы показывает, каков фазовый сдвиг между напряжением на входе и выходе, или между током на входе и выходе в согласованном режиме (не путать с фазовым сдвигом между напряжением и током)
показывает, во сколько раз величины тока и напряжения на выходе четырехполюсника меньше, чем соответствующие значения на входе, т.е. во сколько раз затухает сигнал, проходя через четырехполюсник, работающий в согласованном режиме. Коэффициент фазы показывает, каков фазовый сдвиг между напряжением на входе и выходе, или между током на входе и выходе в согласованном режиме (не путать с фазовым сдвигом между напряжением и током)
2.6. Параметры холостого хода и короткого замыкания
В расчетах используются также параметры холостого хода 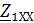 ,
, 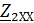 и короткого замыкания
и короткого замыкания 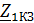 ,
, 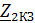 , измеренные соответственно со стороны первичных и вторичных зажимов, которые связаны между собой соотношением:
, измеренные соответственно со стороны первичных и вторичных зажимов, которые связаны между собой соотношением:
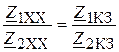 . (25)
. (25)
Характеристические параметры выражаются через параметры холостого хода и короткого замыкания:
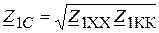 ,
, 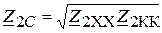 (26)
(26)
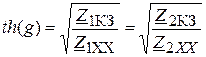 . (27)
. (27)
Сопротивления холостого хода и короткого замыкания определяются через характеристические параметры или коэффициенты 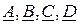
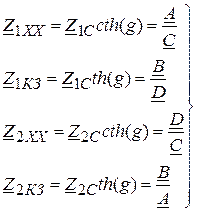 (28)
(28)
Коэффициенты 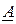 четырехполюсника вычисляются по сопротивлениям холостого хода и короткого замыкания:
четырехполюсника вычисляются по сопротивлениям холостого хода и короткого замыкания:
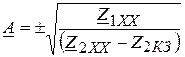 ;
; 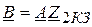 ;
; 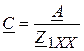 ;
; 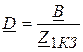 . (29)
. (29)
Пассивный линейный четырехполюсник можно заменить Т– или П – образной схемой замещения. На рис. 3 приведена Т-образная схема замещения.
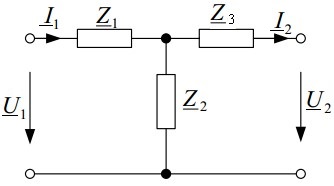
Рис.3. Т-образная схема замещения четырехполюсника
Параметры – коэффициенты 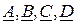 Т – образного четырехполюсника определяются по [2]:
Т – образного четырехполюсника определяются по [2]:
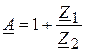 ;
; 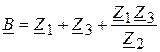 ;
; 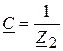 ;
; 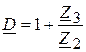 . (30)
. (30)
На рис.4 представлена П – образная схема замещения четырехполюсника
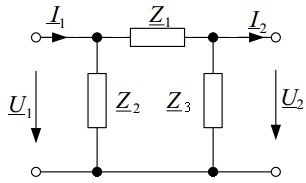
Рис.4. П-образная схема замещения четырехполюсника
Параметры – коэффициенты 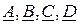 П – образного четырехполюсника определяются по следующим формулам [2]:
П – образного четырехполюсника определяются по следующим формулам [2]:
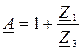 ;
; 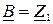 ;
; 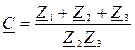 ;
; 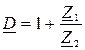 . (31)
. (31)
2.7. Симметричные четырехполюсники
В частном случае при наличие симметричного четырехполюсника, все приведенные выше формулы упрощаются, если учесть, что при этом имеются равенства:
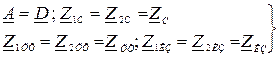
2.7. Эквивалентность четырехполюсников
Четырехполюсники эквивалентны, если они имеют одинаковые: а) параметры коэффициентов одной из форм основных уравнений 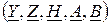 , либо б) характеристические параметры, либо в) параметры холостого хода и короткого замыкания.
, либо б) характеристические параметры, либо в) параметры холостого хода и короткого замыкания.
 2017-11-01
2017-11-01 581
581








