Методом Гаусса исследовать и решить данные системы. В случае бесконечного множества решений найти общее решение и одно какое-либо частное решение

1.

 

 

2.

 

3.

 

4.

 

5.

 

 

6.

7.

 

8.

 

9.

 

10.

 

 

11.

 

 

12.

 

 

13.

 

 

14.

 

15.

 

16.

17.

18.

 

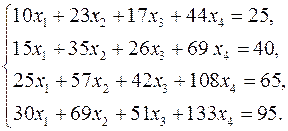
19.

 

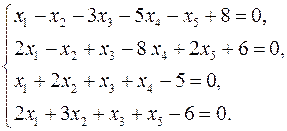
20.

21.

 

22.

 

 

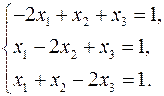
23.

 

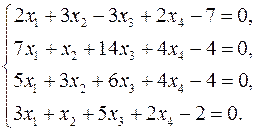
24.

 

25.

 

 

26.

27.

 

28.

 

29.

30.

 

3. Коллинеарны ли вектора и ?

п/п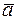
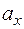
		-2				-1			-1
				-2						-1
	-2				-2					-1
			-3		-1	-1				-1
							-2			-2
			-2			-1
		-2			-1			-2	-2
			-1		-1			-3	-2
	-2	-3	-2						-1	-3
	-1				-2			-1	-6
			-1					-1	-6
			-2		-2			-2
	-2		-1	-3
					-3			-2	-2
	-1		-1		-7			-2	-3
			-2					-1	-1
			-2					-3	-10
			-1					-1	-4
		-1						-2	-2
		-2						-3	-2
						-1				-7
		-1			-7	-6		-3		-2
		-1	-2					-2	-6
	-9					-2		-1
					-1		-3			-3
		-1		-1				-2		-5
				-3				-4	-9
	-1				-1			-2	-3
			-7			-3		-3	-2
			-5		-3			-5		-2

 

 

4. Исследовать на линейную зависимость систему векторов

п/п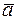
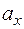
					-1
		-3			-1			-4
		-1		-1		-1		-1
			-5			-2		-1
			-4			-2			-3
		-6			-5	-2		-1
			-3			-4		-3
				-5
	-2				-3			-1
					-1			-1	-2
				-1		-1
									-1
				-1		-1
		-1	-3
					-2
			-1		-1				-1
					-2
									-1
					-3	-7
				-2		-1
		-2						-6
				-1	-2	-1
				-1	-2	-1
									-1

 

5. Написать разложение вектора 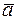по векторам .

 

п/п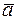
	-2									-1
			-1					-1			-1
		-4				-1					-1
	-9								-3	-1
	-5	-5		-2					-1
								-1				-1
	-19	-1					-2
		-3									-1
			-1				-1			-1
	-1		-4	-1								-1
			-14					-3				-1
		-1			-2		-1
							-1				-1
		-1							-2
			-3				-1					-3
									-1			-1
						-1				-1
	-9	-8	-3				-3				-1
	-5		-13			-2		-1
	-15								-1	-1
								-2
		-14	-30					-1		-3
	-1							-1			-1
		-1			-1					-1
		-8			-2				-1
		-7	-13					-2		-1
								-2
		-20	-1						-1		-3

 

 

6. Найти собственные значения и собственные векторы матрицы:

.

 

п/п
		-2	-1	-1		-1		-2
		-1		-1				-1
		-1				-1		-1
		-1	-1			-1		-1
		-2	-1	-1		-1		-2
			-1			-1	-2
			-1			-1	-1
							-1
							-1
			-1	-2		-1	-2
		-4
		-2			-1			-2
		-2
		-2
		-4
		-6			-1			-2
		-6
			-2			-6		-2
	7/3	2/3	-2/3	4/3	5/3	-2/3
				2/3	7/3	-4/3	2/3	-2/3	5/3
						-1		-1
	19/3	2/3	-2/3			-2	2/3	-2/3	11/3
			-1			-2		-1
			-1			-1
						-1		-1
			-1			-2		-1
		-2	-2	-2/3	5/3	-2/3	-2/3	2/3
	5/3	-2/3	-4/3				-2/3	2/3	7/3
		-4	-2	-2		-2
		-3	-3

 

Общее решение однородной системы

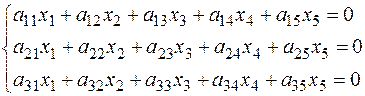
Выразить через какую-либо фундаментальную систему решений.

п/п
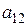
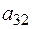
			-8				-2	-3	-7				-12		-5
			-1	-2			-3		-1	-1
					-1		-1		-2			-3	-12	-4
		-9		-3	-12	-4		-14				-3		-1	-4
		-1		-1				-3	-2	-1			-4	-5	-1
		-2		-4	-1			-3		-5				-2	-6
		-1			-1		-2			-2				-1
							-1			-5			-1	-6	-1
		-1		-1	-1			-1					-6
	3/2	5/4	5/7			3/5	1/2	2/7	2/5		1/5	1/6	2/21	2/15
				-1			-3	-2		-3				-2
			-1		-1		-2		-10
		-14		-1			-2		-3			-10			-1
					-1		-2	-5	-3			-2			-1
				-1	-1			-2	-1	-2				-2	-1
			-3		-1		-1		-1			-2		-2
			-3		-1		-2		-10				-9		-3
			-1				-2		-5	-7		-1			-2
		-2	-3	-7				-12		-5		-5		-16
			-8					-12	-34	-5		-5		-16
			-5		-1		-2	-3	-7			-5		-16
			-1					-2					-2
			-5		-1		-2	-3	-7			-5		-16
			-2					-3					-1	-2	-3
		-5					-4						-4	-6
				-2					-1					-5
				-2					-4					-6
								-1
		-1		-2				-2	-1			-3		-3

 

8. Найти расстояние от точки до плоскости, проходящей через три точки , , .

Вариант
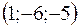
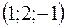
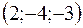
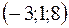
			12  Сейчас читают про: Элементы поперечного профиля дороги II этап сестринского процесса: сестринская диагностика ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ СЕСТРИНСКОГО ПРОЦЕССА В ДЕЯТЕЛЬНОСТИ МЕДСЕСТРЫ Техника наложения бинтовых повязок Модели отношения врач – пациент Столыпинская аграрная реформа Самый сильный аргумент, почему эволюция человека не могла быть В стремлении к важной цели не старайтесь быть деликатным или умным. Воспользуйтесь молотом для вколачивания свай. Врежьте по цели один раз. Вернитесь и ударьте снова. Затем ударьте в третий раз – сильнейшим ударом сплеча… © Черчилль ==> читать все изречения... 8259 8174 Понравился сайт? Поделись им с друзьями: