Подробный расчет теплообменного аппарата в турбулентном режиме

Теплоотдача в трубах

По (/1/, табл. 4.1, стр. 151) находим, что теплоотдача для раствора NH₄NO₃ описывается уравнением:

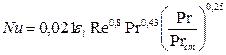, (3.31)

где 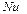- критерий Нуссельта; 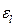- поправочный коэффициент; Re – критерий Рейнольдса; Pr – критерий Прандтля; 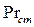- критерий Прандтля при температуре стенки трубы.

Коэффициент 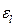примем равным 1, полагая, что 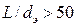(/1/, табл. 4.3, стр. 153), где 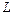- длина труб, 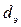- эквивалентный диаметр. Критерий Рейнольдса рассчитываем по формуле:

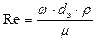, (3.32)

где 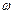- средняя скорость потока, 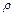и 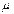- соответственно плотность раствора и динамический коэффициент вязкости, при средней температуре .

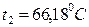По формуле (3.7) и (3.8) находим плотность раствора пр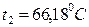и и :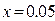

,

.

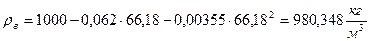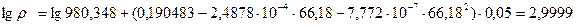
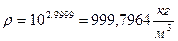Среднюю скорость потока определяем по формуле:

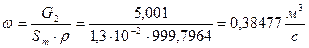
Учитывая, что для труб круглого сечения диаметр труб и эквивалентный диаметр совпадают, то для труб 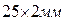получаем:

.

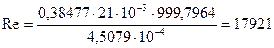Критерий Прандтля находим по формуле:

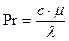, (3.33)

где 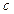- удельная теплоемкость, 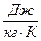; 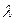- коэффициент теплопроводности, 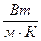; 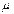- динамический коэффициент вязкости, .

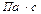Коэффициент теплопроводности пр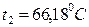и и 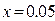определяется по формуле:

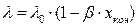(3.34)

где 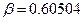, 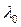- коэффициент теплопроводности воды, :

,

,

.

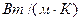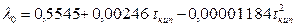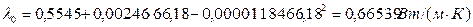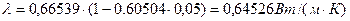Таким образом, критерий Pr пр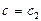и и 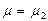равняется:

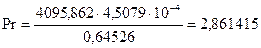
Коэффициент теплоотдачи от раствора к стенке:

.

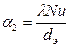С учетом формулы (3.31) получаем:

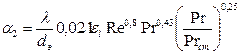, (3.35)

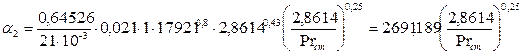. (3.36)