Содержание контрольной работы

Введение

Контрольная работа по курсу «Водоснабжение и водоотведение» относится к числу первых, выполняемых студентами по специальным дисциплинам. Цель работы состоит в том, чтобы привить студентам навыки самостоятельного решения задач, встречающихся в практике инженера-строителя. Выполняя контрольную работу, студенты используют знания, приобретенные при изучения курса «Гидравлика», реализуют их на практике, что является важнейшим условием стимулирования познавательной деятельности.

Задача контрольной работы состоит в выполнении некоторых часто встречающихся гидравлических расчётов напорного трубопровода и подборе насосной установки.

СОДЕРЖАНИЕ КОНТРОЛЬНОЙ РАБОТЫ

Контрольная работа по курсу включает в себя:

1) выбор экономичных диаметров трубопроводов, подводящих жидкость к потребителям и магистрального трубопровода.

2) определение потерь напора по участкам и в системе в целом.

3) построение характеристик отдельных ветвей трубопровода и системы в целом.

4) подбор центробежного насоса и совмещение характеристик насоса и системы трубопровода (нахождение рабочей точки).

5) определение допустимой геометрической высоты всасывания.

Пояснительная записка к курсовой работе должна быть выполнена на стандартных листах (формат № II), либо в отдельной тетради, расчетно-графические материалы на миллиметровой бумаге.

Объем пояснительной записки 10-15 листов.

При использовании литературных источников, обязательно давать список литературы, давая полное наименование и все библиографические сведения.

2. ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ РАСЧЕТА ТРУБОПРОВОДОВ

Одной из главных задач гидравлического расчета трубопроводов является определение напора, скорости и некоторых других величин при заданных условиях движения. Для решения многих задач, связанных с расчетом системы трубопроводов, используется уравнение Бернулли:

где Z₁ и Z₂ – высоты центров тяжести выбранных сечений 1 и 2 над плоскостью отсчета;

пьезометрические высоты в выбранных сечениях;

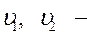скорости движения жидкости в м/с;

коэффициенты Кориолиса;

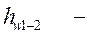потери напора на участке 1-2.

При расчете открытых русел произвольного сечения широко используется формула Шези:

где С – коэффициент Шези (скоростной множитель);

R – гидравлический радиус;

i – гидравлический уклон.

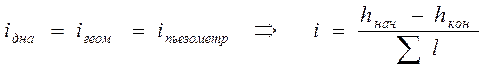
Коэффициент Шези может быть определен по формуле Павловского:

где n – коэффициент шероховатости, зависящий от состояния стенок трубопровода;

y – показатель степени.

Для 0,1 < R < 3 м

Показатель степени y можно определить по упрощенным формулам:

Коэффициент шероховатости n в зависимости от состояния стенок трубопровода принимается:

Новые стальные и чугунные трубы – = 0,01

Водопроводные трубы в нормальных условиях эксплуатации – = 0,012

Загрязненные водопроводные трубы – = 0,013-0,014

Значение коэффициента Шези С может быть вычислено из таблицы (1).

Формула Шези (2) может быть представлена в виде:

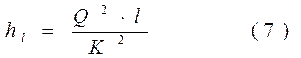
где h_l – потери на трение по длине трубопровода;

Q – расход жидкости;

l – длина трубопровода;

K – расходная характеристика.

Значение расходной характеристики K (в л/с) может быть взято из таблицы 1.

Значение расходной характеристики.

Таблица 1

Условный проход в мм	К
n = 0,0111	N = 0,0125	n = 0,0143
40	5,306	4,666	4,083
50	9,362	8,460	7,403
75	28,37	24,94	21,83
100	61,11	53,72	47,01
125	110,6	97,40	85,23
150	180,2	158,4	138,6
175	271,8	238,9	209,0
200	388,0	341,0	298,5
225	531,2	467,0	408,6
250	703,5	618,5	541,2
300	1144	1006	880,0
350	1726	1517	1327
400	2464	2166	1895
450	3373	2965	2594
500	4467	3927	3436
600	7264	6386	5587
700	10960	9632	8428
750	13170	11580	10130
800	15640	13750	12030
900	21420	18830	16470
1000	28360	24930	21820

Формула Шези (2) и получаемая из нее формула (7) соответствует условиям вполне шероховатой (квадратичной) зоны движения, когда сопротивление по длине не зависит от числа Рейнольдса.

Общей формулой при расчете трубопроводов, работающих в области как ламинарного, так и турбулентного режимов течения является формула Дарси:

где λ – коэффициент гидравлического трения (коэффициент Дарси).

Формулы (2) и (7) могут быть получены как следствие формулы (8).

Значение коэффициента гидравлического трения λ могут быть взяты по графикам Никурадзе [1] или Мурина [1,2], или определены по формулам в зависимости от зоны движения.

Зона 1 – ламинарный режим движения Re < 2320.

- формула Пуазейля

Число Рейнольдса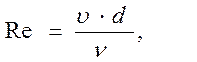

где ν – кинематический коэффициент вязкости.

Зона 2 – турбулентный режим течения в гидравлически гладких трубах (зона гидравлически гладких труб)

где ∆_э – эквивалентная шероховатость трубопровода [2].

- формула Блазиуса.

Зона 3 – переходная область от турбулентного движения жидкости по гидравлически гладким трубам к турбулентному движению по гидравлически шероховатым трубам

- формула Альтщуля.

Зона 4 – турбулентный режим движения в шероховатых трубах (квадратичное сопротивление)

- формула Мурина

Для определения коэффициента гидравлического трения имеется ряд обобщенных формул, действительных для всех областей турбулентного режима течения. Широко используется формула Кольбрука:

Значения эквивалентной шероховатости могут быть взяты из [2] или по

таблице 2.

Значения эквивалентной шероховатости.

Таблица 2

№ п/п	Материал и состояние труб	∆_э, мм
1	Из стекла и цветных металлов, новые	0,001 - 0,002
2	Стальные бесшовные, новые	0,01 – 0,02
3	Стальные сварные, новые	0,03 – 0,10
4	Стальные сварные, умеренно заржавевшие	0,30 – 0,70
5	Чугунные, новые	0,20 – 0,50